空化射流型单倾角叠片式清洗器流场模拟与结构优化

李可为，王雨晴，徐琴琴，任泓睿，银建中

大连理工大学化工机械与安全学院，辽宁大连116024

流程工业中存在大量输送管道，其运行过程中的结垢、淤堵和腐蚀问题非常普遍[1]，这些管道多埋于地下，清洗和安全不容忽视[2−3]。已有的清洗方法都存在一些不足，比如化学清洗药品会腐蚀管道，物理清洗操作复杂、条件苛刻。因此发展一种高效便捷的清洗技术非常必要。

空化清洗方法[4]利用空化气泡产生、溃灭过程所产生的高温、高压射流作用于污垢表面使其开裂、分解、破碎，从而实现管道清洗。研究发现，空化撞击力还能强化材料表面性能，延缓进一步结垢的时间[5]。

射流空化法用于管道清洗已有文献报道[6−7]，就是将叠片式清洗器置入管道中，利用高压水流（约0.5~2.0MPa）推动其在管道中运动。当水流穿过叠片型清洗器叶片与管道间的缝隙时，水流速度增大，压力降低，当压力低于水的饱和蒸汽压时，会产生空化现象。空化气泡破裂会产生强大的机械作用力，这种力以高冲量的机械能作用于污垢表面并使其破裂并将其击碎，进而冲刷后排出管道实现清洗。

空化射流清洗方法有如下优势：1）操作简单无污染；2）安全可靠；3）清洗距离长；4）除垢效果明显。本文基于CFD模拟，着重研究射流空化清洗器的流场分布、空化强度与清洗器结构间的关系，进而探讨不同管径时清洗器的结构设计问题。

1 模型建立

文献中已有对清洗器基本结构优化的设计[8−9]，而本文主要探究如何根据管径改变调整叠片型清洗器的结构尺寸。根据参考文献[10−11]中已有的叠片型清洗器结构，建立清洗器的整体结构如图1（a）所示，截取清洗器的入口截面如图1（b），该截面中叶片结构的局部放大如图1（c）。适用于70mm管径管道的清洗器的清洗叶片宽14mm，厚1mm。由于清洗器内外层的24个叶片相错排列，可根据对称性选取清洗器的1/12结构进行建模。

图1 入口截面示意

本文主要研究叶片与管壁之间的空化情况。考虑到完整模型结构复杂、计算工作量大，为了提高计算效率，将清洗器中间部分去除掉，同时将2组叶片简化为1组，再以其中一种缩放形式的完整模型验证简化模型的准确性。本文利用Gambit软件进行模型建立及网格划分，如图2所示。该模型中，清洗器叶片倾角为79°，轴向长度35mm，叶片前端距管道入口12mm。

图2 三维模型

计算模型的选择上，本文使用了计算相变情况下有更高准确度的mixture多相流模型，湍流模型使用标准k-ε模型。选用SIMPLE耦合算法，方程的离散格式除压力项选用PRESTO!格式外，其余皆为一阶迎风格式。在边界条件的设定上，设定管出入口为压力边界，入口压力为0.5MPa，出口压力为大气压。

在研究对应不同管径下清洗器结构的合理性时，以清洗器工作时产生空化现象的气相分布云图为评判依据。从云图中能直观判断空化泡的数量，为定量表示空化区域长度，本文将全流场气体含量百分数沿管长方向做图，提取气相产生的左右端点，其间隔作为空化区域的长度。基本参考模型（即管径为70mm的模型）气相云图如图3所示，气体出现的部位在叠片型清洗器入口叶片与管壁之间，提取其气相长度为16mm。模拟结果与文献[5]中的实验一致。以此为评价依据对不同管径下清洗器尺寸进行设计。

图3 气相分布云图

2 不同管径的推广

当推广到不同管径时，采取2种设计方法。其一，按照等比例缩放原则，将叠片型清洗器所有尺寸根据实际管径与基本模型管径（D=70mm）间的比值进行等比例放大或缩小，得到空化区域长度与基本模型（D=70mm）清洗器空化区长度间的关系。其二，保持入口处叶片与管道内壁间的缝隙不变，如图4所示。

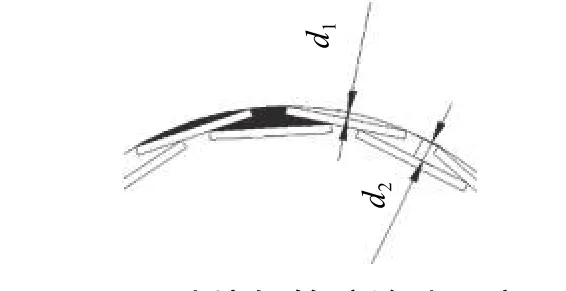
图4 叶片与管壁缝隙示意

保持内外叶片与管壁间缝隙不变，同时兼顾相邻叶片间距适当，按比例缩放叶片后并进行圆整获得清洗器结构尺寸。对上述2种情况分别进行模拟，选取管径分别为50、60、70（基本模型）、80和90mm的5个规格。同时为了保证标准的可靠性，在建立不同规格的模型时，设置的边界条件仍与基础模型（D=70mm）相同。

2.1 等比例缩放模型

根据D=70mm的基础模型等比例缩放，适用于管径为50、60、80、90mm的清洗器产生空化现象的气相分布云图如图5所示。

图5 等比例缩放对应管径的气相分布云图

由图5可以看出，等比例缩放后，气相分布情况与管径70mm的情况基本一致。分别提取其气相百分比沿管长方向的分布，得到空化区域气相分布长度分别为12、14、16、18和20mm。

图6 等比例缩放空化区域长度与管径的变化关系

如图6所示，若采用等比例缩放法改变清洗器尺寸使其适用不同管径的管道，其产生的空化区域长度将与管径呈线性关系。这是因为当清洗器尺寸随管径等比例缩放时，叶片外缘到管壁的间隙也随之等比例改变，当其他条件不变时，可认为是在误差范围内清洗器工作产生的空化区域长度正比于间隙尺寸。

进一步分析，取管壁的一条直线，如图7所示；每种情况下的气相分布情况，如图8所示。

图7 提取直线位置

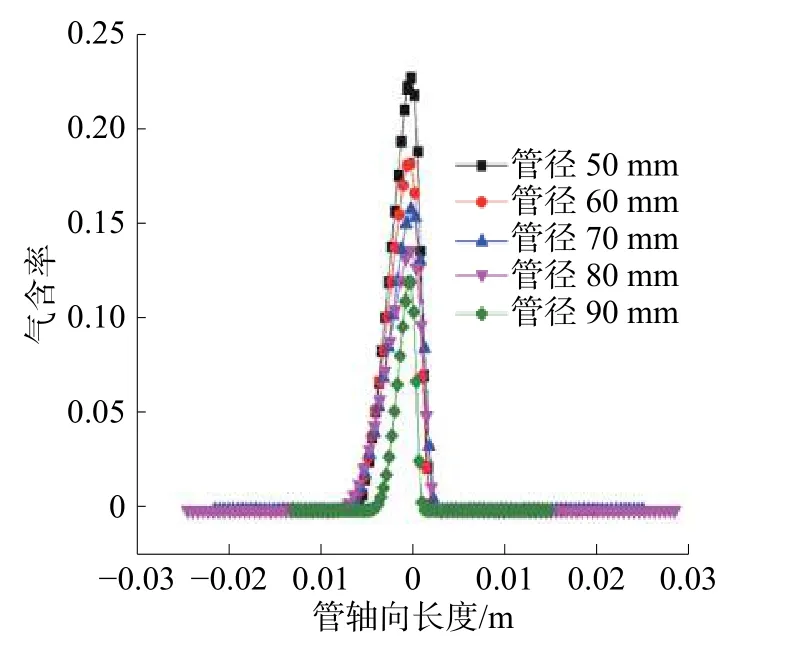
图8 等比例缩放气相分率沿直线的分布情况

图8展示了不同规格的清洗器沿同一条路径的气含率分布规律的相似性。气相产生的部位只是在长度和数值上有所不同：当清洗器尺寸适应管径等比例增大时，而气相区域长度增加，最大气含率值降低。

图9展示了不同规格的清洗器沿同一条路径的压力分布规律。对比压力分布和气相分布可以看出，气相产生区域与低压区一一对应。

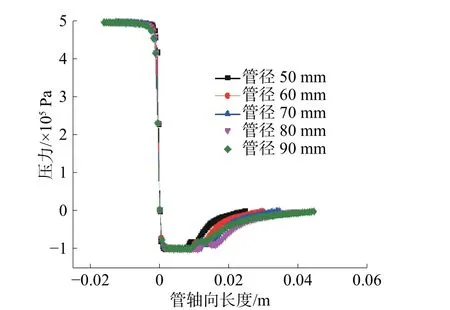
图9 等比例缩放压力沿直线的分布情况

2.2 等间隙缩放模型

不同于等比例缩放模型，等间隙缩放即在改变清洗器尺寸以适应不同管径管道时，保持清洗器叶片外缘与管壁的间隙不变。保证d1和d2不变，可计算得管径50、60、80和90mm对应的清洗叶片数分别为9、10、15、16，对应叶片轴向长度分别为25、30、40和45mm。对等间隙缩放模型下各规格清洗器的工作状况进行模拟，得到如图10所示的空化气相分布云图。

图10 等间隙缩放不同管径的气相分布云图

分别提取其气相百分比沿管长方向的分布，得到管径50、60、70、80和90mm对应清洗器产生的空化区域长度分别为14、14、16、19和15mm。空化区域长度与管径的关系如图11所示。

由图11可以看出，保持缝隙不变，空化区域长度与管径的关系较为复杂，各个管径下的气相长度与管径70mm时长度接近，在小范围内波动。分析波动的原因，虽然控制缝隙一致，但由于管径弧度的问题，不可能做到所有的缝隙完全一样，因此空化区域长度接近，而不完全一样。

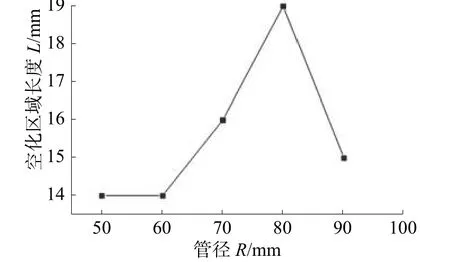
图11 等间隙缩放空化区域长度与管径的变化关系

在同样的位置提取直线进行分析，对比直线上的气相分布情况如图12所示。

图12 等间隙缩放气相分率沿直线的分布情况

由图12可知，当缝隙不变时，不同管径气相云图的最大值有区别，分布不均匀，气相分布情况与基础模型情况成波动关系，分析可能的影响因素在于一周的叶片数不同。

其压力分布情况如图13所示，与等比例相似，低压区与气相区域相对应。

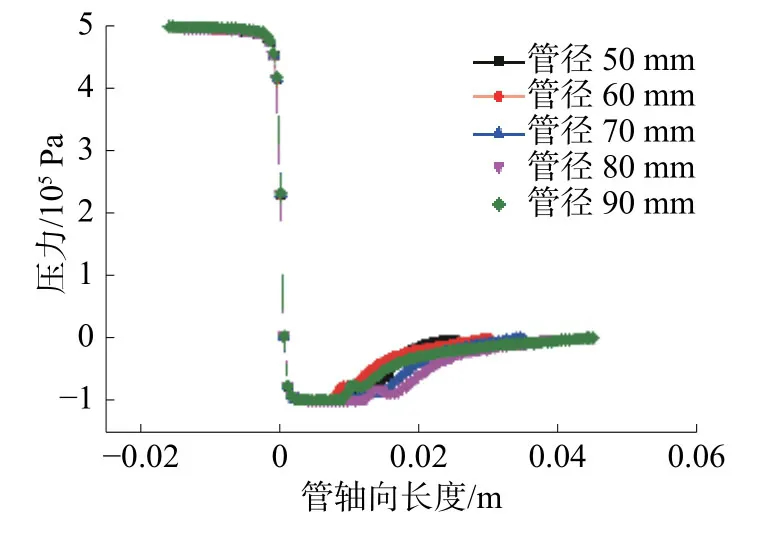
图13 等间隙缩放压力沿直线的分布情况

3 完整模型验证

为了验证简化模型的准确性同时也验证其他尺寸和操作条件下得出的结论是否适用，以一种结构的完整模型做验证，其模型网格图如图14所示。

图14 完整模型网格图

参考模型对应的管径为56mm，改变管径并将清洗器进行等比例缩放，得到管径为40、48、64、72mm时的清洗器模型。设定入口边界条件为速度入口，速度5m/s，出口为压力出口，压力仍为大气压。模型算法设置与简化模型一致，作出各个管径下的水蒸气相云图，如图15所示。

图15 不同管径下稳态的水蒸气相云图

仍以清洗器工作时产生的空化区域长度为评判标准，得到如图16所示的不同管径下对应清洗器空化区域长度的关系曲线。可以看出，与图6所示规律相同，不同清洗器尺寸下空化区域长度随对应管径正比增加，因此在以空化区域长度作为评价标准的情况下，根据管径等比缩放清洗器尺寸的方法同样适用于完整模型。

图16 完整模型空化区域长度与管径的变化关系

上述研究表明，当评价清洗器工作状况的标准为空化区域长度时，等比例缩放法在完整模型与1/N简化模型下得到的结论一致。

4 结果分析

综合分析第2章结果，不管是等比例缩放还是等间隙缩放，都可以看出气相范围主要集中在入口处，即空化场主要位于叶片入口处。同时由压力和气相对应分布图可以看出，低压区和气相一一对应，但是同样的压力对应的气相百分比不同，分析原因可能因为低压是产生气相的基础，而气相的多少要结合周围流场边界等各个条件综合考虑。将2种缩放方法得到的不同管径下对应尺寸的清洗器工作产生的空化区域长度进行对比，如图17所示。

图17 等比例缩放与等间隙缩放改变管径后结果对比

可以看出，使用等比例缩放改变清洗器尺寸时，清洗器工作产生的空化区域长度随管径呈线性变化关系，而等间隙模型随着管径小范围波动（由于结构的要求，没有办法保证完全缝隙一致）。由2种设计方法的规律以及工业管道的管径范围可得：当管径缩小时，采用等间隙法可得到更长的空化区域；而当管径变大时，采用等比例法可得到更长的空化区域。由图可以观察出，当缝隙不变时空化的长度变化不大；而当等比例缩放时，由于缝隙的大小也等比例缩放，因此空化区域长度也随着等比例缩小或扩大。由此可得出，空化区域长度主要和缝隙有关，在保证缝隙足够产生空化的情况下，缝隙变大，有利于空化长度的增加。

5 结论

由上文分析可得到以下结论：

1）当高压水流流过叶片时，会产生压力降，低压区与气相产生的区域相对应。管径改变时，压力与气相区域对应结果相似，只是数值上存在差异。

2）在对其他不同管径下的除垢器进行设计研究发现：管径更小时，保持等间隙缩放设计的清洗器产生的空化效果更好；管径更大时，采用等比例缩放设计的清洗器有更好的空化效果。

3）空化的区域长度范围主要和缝隙有关。当缝隙足够产生空化时，增大缝隙可以扩大空化范围，这一结论对之后叠片型清洗器的设计有指导作用。

本文对管径改变时清洗器的设计提供了2种可行性方案，具体实际操作过程需要进一步研究。