基于细粒度指纹的室内定位系统

田熙燕， 杜留锋

1.河南科技学院机电学院，河南新乡453003 2.南京邮电大学通信与信息工程学院，南京210003

伴随无线感知技术的发展，室内基于位置服务（location-based services,LBS）的需求如物流仓库货物管理、医院特护病人跟踪等急剧增长，室内无线定位技术受到了广泛关注.而室内普遍的非视距（non line-of-sight,NLoS）环境导致信号在传输中更易受到多径效应和阴影效应等负面影响.因此设计一个精度高、鲁棒性强且实时的室内定位系统非常必要.

近年来，基于Wi-Fi 的指纹定位技术越来越受到关注，主要受益于两点：1）相对于几何测量法，指纹技术受NLoS 影响较小，能满足大部分LBS 的精度要求；2）大多室内场所已遍布无线访问点（access point,AP），Wi-Fi 信号覆盖率高.此外，由于Wi-Fi 接收信号强度（received signal strength indicator,RSSI）可在大多的移动终端上被采集，无需额外的硬件[1]，因而RSSI 成为了首选的位置指纹.然而，RSSI 是数据包级的功率参数，在复杂的室内场景下，其描述能量强度-收发间距（能-距）关系时常呈现出较大的随机性，这使得基于RSSI的定位系统难以满足更高的要求[2].

目前，融合正交频分复用（orthogonal frequency division multiplexing,OFDM）、多入多出（multiple-input multiple-output,MIMO）和信道绑定等技术的IEEE 802.11n[3]已成为WLAN 的主导标准.在Wi-Fi 常用的2.4GHz/20MHz 信道模式下，OFDM 调制的子载波（子信道）数达到了56 个（52 个用于传输数据），如图1所示.利用修改固件后的无线网卡（如Intel 5300[4]、Atheors 9k[5]）可以解析出子载波的频响采样值，这些采样值即为信道状态信息（channel state information,CSI）[4].CSI 表征了信道的频率分集，提供了子载波频域下的幅度和相位值，细粒度级地刻画了物理层.此外，CSI 分别对MIMO 下不同天线对的子载波进行记录，使其同时具备了表征信道空间分集的能力.因此，相比于RSSI，CSI 具有更小的时间波动，能-距表达更稳定[6].

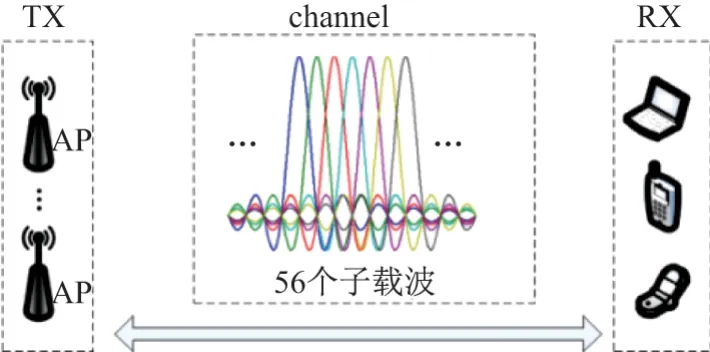
图1 IEEE 802.11n (2.4 GHz/20 MHz)下Wi-Fi传输模型Figure1 Wi-Fi transmission model in IEEE 802.11n standard (2.4 GHz/20 MHz)

1 相关工作

近年来，一些将CSI 作为位置指纹的系统在定位的精度和稳定性上均得到了较好的结果.较早的PinLoc 系统[7]在Wi-Fi 环境下借助解析出的原始CSI 以接近0.9 的概率实现了米级精度.但其在离线阶段需对划分的全部采样位置点进行指纹收集，工作量较大.最近提出的FIFS[8]、CSI-MIMO[9]及DeepFi[10]方案均利用了CSI 的频率分集和空间分集，大大提高了指纹的稳定性.在指纹的设计上，FIFS 将各子载波的多个原始CSI 进行幅度平均，然后进行子载波叠加生成指纹；CSI-MIMO 对聚合了CSI 幅度和相位信息的矩阵进行前向差分，生成一个混合指纹.在线定位阶段的两系统均基于贝叶斯准则在设定的场景下取得了约1 m 的精度.DeepFi 利用深度学习模型尝试了用深层网络的权值表征指纹的工作.其在离线阶段选取CSI原始幅值作为输入训练网络，在线阶段基于径向基函数实现指纹匹配.DeepFi 借助深层网络的强非线性拟合能力取得了较优结果，但需要巨大的训练成本.

位置指纹是决定系统性能优劣的根本，理想指纹应具备同采样点波动小、异位置区分度大的特征.CSI 受限于目前主流Wi-Fi 的信道带宽，文献[2,11]指出如不对指纹精心设计，基于CSI 系统的精度很难触及米级以下.鉴于此，本文首先从CSI 原始值的预处理入手，设计了一种较优的指纹构造方法；其次，将采样点划分后的定位区域，抽象为一个位置-指纹矩阵（location-fingerprint matrix,LFM），用矩阵元素表示采样点指纹，LFM 即指纹库；此外，为减轻离线阶段全采法构建指纹库的繁重工作[12]，本文基于矩阵完备（matrix completion,MC）[13]理论，提出了离线阶段高效的指纹建库方案.在线阶段借助贝叶斯准则执行了指纹匹配[14]；最后在两个典型的室内环境下对所提方案进行了评测，实验的结果显示了提案的优良性.

2 位置指纹构造

2.1 CSI

室内无线环境下，利用IEEE 802.11n 接收终端及802.11n-CSI Tool[15]可获取表征通信链路子信道的CSI，表示为

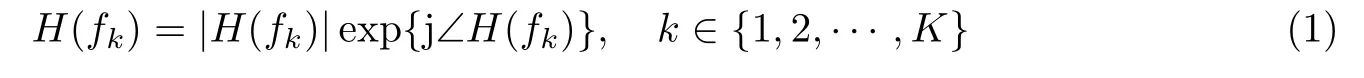
式中，H(fk)表示中心频率为fk的第k条子载波（子信道）的CSI；|H(fk)|表示子载波的幅度，∠H(fk)为相位.本文采用的终端为Intel 5300，在2.4 GHz/20 MHz 模式下，一个接收Packet 中可解析出30 个子载波的CSI，即K= 30.在MIMO 下，每对TX/RX 链路的天线组合均是一个空间信息流.因此，子载波k的CSI 可进一步表示为复矩阵

N和M分别代表发送天线（transmitting antenna,TA）和接收天线（receiving antenna,RA）的个数，当前主流MIMO 技术下N ∈{1,2,3}，M=3.Hn,m表示第n个TA 到第m个RA 天线对的CSI.不同天线对代表不同路径，故式(2)中元素相异.

CSI 充分利用了MIMO-OFDM 的频率和时空分集，在对抗室内干扰时能呈现很好的鲁棒性.在空间区别度上，文献[7]已经证明了间隔1 m 的相异采样，采集的CSI 组合值具有很低的相关性.因此，CSI 十分契合位置指纹的核心要求.

2.2 CSI 有效值

无线终端初步获取的是一种表征值，称为CSI 原始值.本文结合接收Packet 中的RSSI、接收噪声及AGC 增益等信息，设计了一种相较原始值更稳定的表征值，称为CSI 有效值.转换方式如下：

式中，Heff为CSI 的有效值，Hraw为原始值.η为功率衰减因子，本文测试环境下，TA 数目N ∈{1,2,3}分别对应η ∈{1.0,1.4,1.7}.为M个RA 总的RSSI；Praw为各子载波的原始功率，大小为Hraw元素的幅度平方；为子载波的原始总功率.K=30，ε为量化噪声.

图2给出了静态实验室下，随机选取的4 个采样点L1～L4处CSI 的Hraw与Heff的对比.TA 和RA 分别取2 和3，各采样点收集有效Packets 为1 000 个.图2中，Amplitude 为各天线对CSI 的幅度平均.可以看出，与原始值相比有效值波动更小.基于Heff构造指纹能更有效地削弱NLoS 等引发的负面影响，有利于提高系统的整体性能.

图2 CSI原始值与有效值稳定性对比Figure2 Comparisons of stability between raw and effective values

2.3 CSI 指纹构造

为进一步提高鲁棒性，每个采样点将收集多个CSI，然后再将这些CSI 融合为唯一的位置指纹.目前在MIMO 下融合的方法主要有平均策略[8]和差分策略[9]两种，本文将采用平均策略.此外，尽管目前室内常为多AP 环境，但考虑到AP 不断提高的覆盖能力，以及多AP存在的重叠干扰现象[16]，本文采用单AP 模式.文献[10-11]已证明，在覆盖力足够的前提下，单AP的效率和灵敏度更优.单AP 下采样点指纹表示为

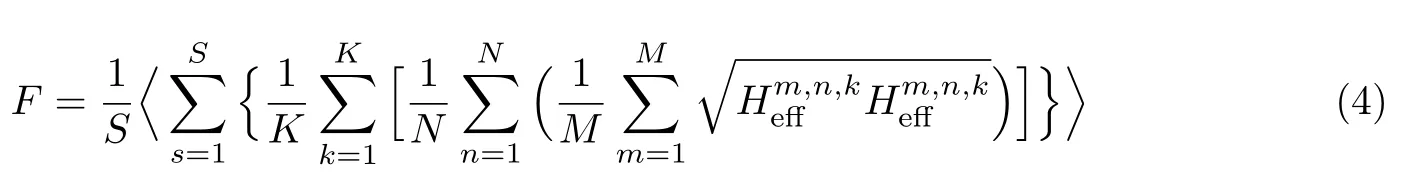
式中，F为融合平均后的最终指纹.S为采集的有效Packets 总数，为CSI 有效值，M、N分别为TA、RA 数量，K为30.

3 指纹库构建

相较于几何法，指纹技术虽具有精度高、稳定性强等优点，但构建指纹库需要繁重的采集工作，严重阻碍了指纹定位的广泛应用.为了有效解决该问题，本节将借助矩阵完备理论来探寻提高建库效率的途径.

3.1 矩阵完备理论

如果元素缺失的矩阵具有低秩特征，且已知的测量值呈均匀随机分布，则通过满足受限等距特性的映射[13]，就能够实现矩阵的精确补全，这一过程即矩阵完备.可描述为

式中，X为目标矩阵，大小W ×L，这里设W≤L；为仅含γ个测量值的待补全矩阵，即测量值矩阵.Ω为测量值位置的集合，|Ω|=γ ＜＜W ×L.本文场景下，为仅含部分位置指纹的LFM，=Fw,l为获取的指纹值；X代表完备后完整的指纹库.

秩最小化算子是非凸的，求解式(5)是一个NP 难问题.由于核范数是秩函数在目标矩阵单位谱范数集合{X ∈RW×L:‖X‖2≤1}上的凸包络，故式(5)可松弛为[13]

式中，‖·‖∗和‖·‖F为核范数和Frobenius 范数.为X第i个奇异值.ξ为噪声.针对许多完备问题，如图像修复、无线传感网内目标定位等，式(6) 满足γ≥αrL1.2lnL后，X将以不低于1-β(L)-3的概率重构[17]，这里α,β ∈(0,1)为环境参数，r为目标矩阵X的秩.

核范数最小化可通过半定规划（semidefinite programming,SDP）求解.近年来一些高效的迭代方法，如奇异值阈值法、奇异值投影法等[17]，陆续应用于完备问题中并取得了很好的结果，这些均为本文的重要理论支持.

3.2 LFM 低秩特性

低秩性是矩阵实现精确完备的必要条件，而秩可以映射为矩阵非0 奇异值的个数.由于实测的LFM 受噪声污染，因而低秩判定可松弛为：近似0 的奇异值占比越小，矩阵低秩属性越强[13].CSI 作为描述能-距关系的参数，具有潜在单调性，因此可推测LFM 的元素间必隐含强相关行为，而这种相关性是低秩的前提，接下来将对该特性进行具体验证.

首先，针对研究室和实验室场景下获取的4 个矩阵（LFMs410、LFMd401、LFMs616和LFMs626）进行奇异值分解如下：

式中，σi为LFM 的奇异值，ui和vi分别为σi的左、右奇异向量.下标40 与66 分别对应教研室和实验室两种场景，上标s 和d 分别对应静态和动态两种环境，1 和2 表示AP 的天线数目.为直观展示奇异值的相对比重，绘制了4 个LFM 各奇异值的占比示意，见图3.

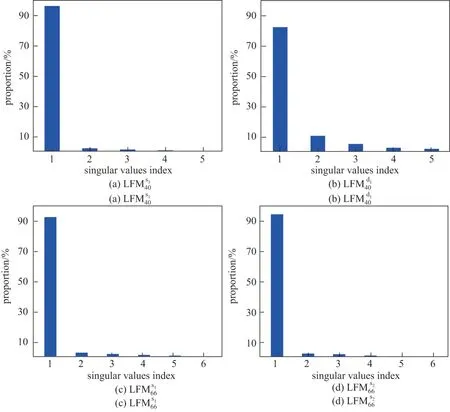
图3 LFM奇异值的占比示意Figure3 Proportion of singular values of LFMs

从图3可以看出，4 个LFM 的大部分能量均来自前位较大的奇异值，各矩阵首个奇异值的占比均超过了80%，由噪声等因素造成的近似0 的奇异值，总体占比很小.而图3(b)的动态场景矩阵，由于干扰较多造成前位奇异值占比相对不高.图3表明了实际场景下的指纹库LFM 具备近似低秩这一先验，从而使得基于MC 的高效指纹库构建成为可能.

3.3 指纹库构建方案

如前述，定位区域与LFM 的关系可表示为图4.

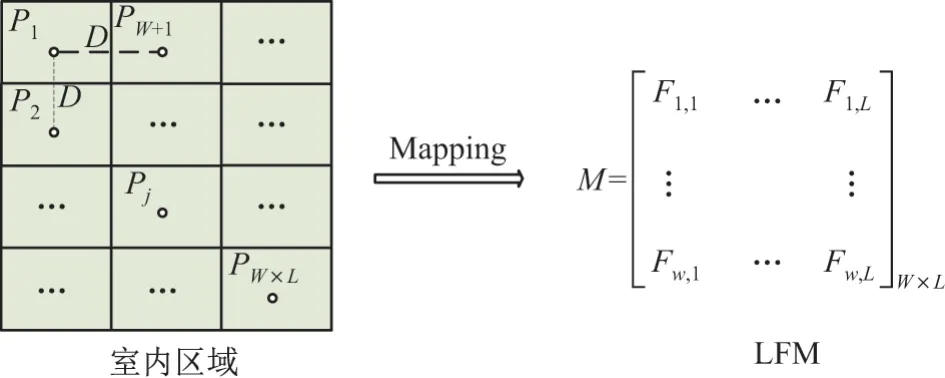
图4 LFM 映射示意Figure4 Mapping illustration for LFM

图4中，D为定位区域相邻采样点的间隔，通常设置为常数.M的行列对应室内的采样点划分，W和L分别表示两个平面方向上的采样点数.令元素Fw,l为采样点pj的指纹值，则任意行列坐标（w,l）与j的关系满足：j=w+(l-1)W.

传统的指纹库构建需要对全部的采样点进行采集，这往往需要巨大的工作量.鉴于LFM满足近似低秩约束，在建库时只对定位区域的少量位置点进行指纹收集，得到一个只含有部分测量值的待补全LFM，如式(8)所示，进而基于MC 理论对该矩阵执行完备运算，最终得到一个完整的指纹库.

式中，对应未采样点的元素设为0，Fw,l符合均匀随机分布，在实际收集过程中所选的采样点应满足这一条件.

显然，所提方案可大大减少离线阶段构建指纹库的工作量，且在大尺度定位区域背景下所带来的效率收益会更明显.而相对于一些传统的数据补全方法，如线性空间插值法等，MC更能充分利用矩阵的低秩性和元素之间的相关性.

4 在线指纹匹配

为实现定位，在线阶段需要将定位请求端（location request terminal，LRT）所采集的位置指纹与指纹库进行匹配.相比确定性匹配技术，基于概率的方法更能准确地提供结果[6].因此，本文设计了一种基于BR 的匹配方法，用以实现LRT 的位置估计.

依据BR，LRT 在未知位置lj的后验概率可表示为

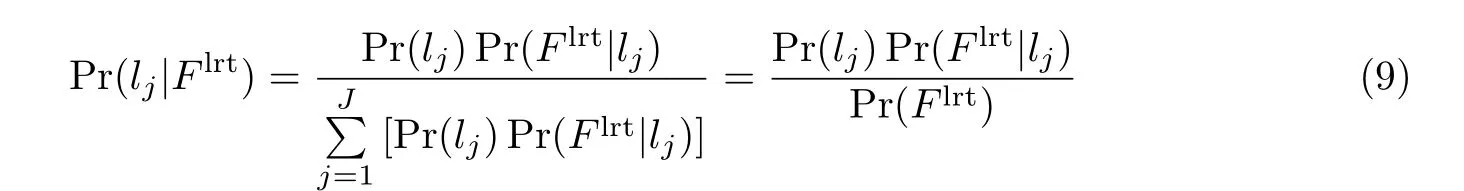
式中，Flrt为LRT 在lj处按照式(4)获得的位置指纹，J=W ×L为采样点总数，Pr(lj)为LRT 处于位置lj的先验概率.不失一般性，设Pr(lj)满足均匀分布，即Pr(lj)=1/J；Pr(Flrt)不包含lj视为常量.因此后验概率问题式(9)转化为求解似然概率Pr(Flrt|lj)，其高斯分布函数的逼近形式可表示为

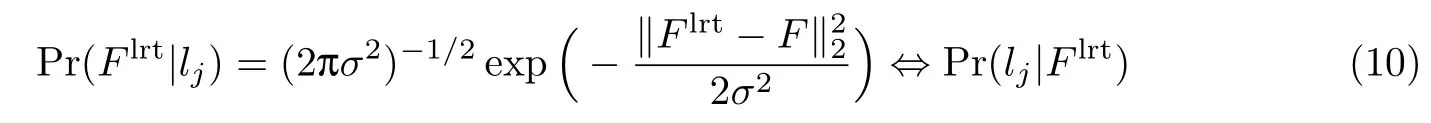
式中，F为LFM 中的指纹值，σ2为方差.利用BR 和高斯模型，LRT 的最终估算位置，将由所有采样点的加权平均表示，即

在线阶段指纹匹配的性能将在下文阐述，其实现过程见算法1.

算法1基于BR 的指纹匹配方法

输入LRT 在线获取的S个CSI 有效packets，指纹库LFM.

输出LRT 的估算位置l.

按照式（4）计算LRT 在线位置指纹Flrt，计算S个CSI 有效值方差σ2；

5 实验结果与评价

本节给出了场景设置；评测了所提指纹库构建方案的精确性和稳定性；综合评测了所提系统的定位性能，并与现有的同类技术进行了比较.

5.1 实验场景

评测的Wi-Fi 工模为2.4 GHz/20 MHz；AP 采用TL-WR 系列的742N、841 N 和882 N，TA 数N分为1、2、3，离地1.5 m；CSI 采集借助集成化平台“Wi-Fi 雷达系统”[19]，RA 数为3，离地1 m，如图5所示.定位场景2 个：教研室和实验室，见图6.为兼顾丢包率和响应速度，离线阶段设置包的Ping 速为：N=1 时每秒100 个，N=2、3 时每秒50 个，在线阶段为每秒100 个.

图5 Wi-Fi 雷达系统Figure5 Wi-Fi radar system

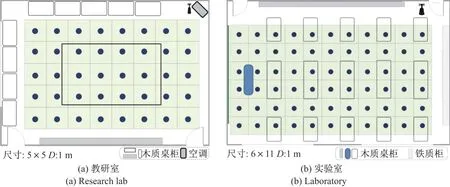
图6 定位场景平面图Figure6 Localization scenario layouts

为进行矩阵完备的效果对比，离线阶段执行全采样点指纹采集，方案见表1.采集过程为静态时，室内无移动目标；采集过程为动态时，室内3 人正常活动.在线阶段无其它移动目标，图5中的可移动RA 作为LRT 执行指纹采集.

表1 指纹采集方案Table1 Fingerprints acquisition scheme

5.2 指纹库构建方案评测

为评测MC 建库方案的有效性及精度，本文首先对完整采集的实测指纹库矩阵按50%、60%、70%和80%采样，以生成对应的待补全矩阵.由于LFM 规模较小且离线阶段对实时无过高要求，因此重构采用精度较高的SDP-based 算法[16]，并借助CVXPY[20]求解.常用的相对重构误差（relative reconstruction error，RRE）和总体重构误差（total reconstruction error,TRE）被作为评价标尺，算式如下：

式中，X、M分别为实测和重构矩阵.不同比例测量值下的重构结果见图7.

生成待补全矩阵时考虑测量值边界参数：5×8时α= 0.4，6×11 对应α= 0.3[16].从整体上讲，图7反映出基于MC 的方案可以实现高效、精准构建指纹库的目的，在仅60%采集工作量下，静态环境时约95%的RRE 低于0.02，如图7(a)和(c)所示；较差的1 TA 动态环境时，低于0.02 的占比也达到了85%，如图7(b)所示；其次，通过图7可知，重构精度与测量值成正比，这与大部分基于MC 的实际应用情况相一致；最后，根据3.2 节，CSI 的能-距关系越稳定LFM 低秩性越强.因此，在指纹定位系统中，重构精度也受制于CSI 的波动性，具体表现在：1）同一场景下，即图7(a)、(b)和(d)，室内人员的随机行为会产生更多干扰，因此静态环境重构精度高于动态；在多TA 下，动态环境造成的不稳定在CSI 平均策略下可得到弱化，故较于(b)，(d)的重构更为精准.2）场景规模越大、环境越复杂，重构精度越不易得到保证，原因仍源自多径、反射及衍射等对CSI 的干扰，而弱化干扰的措施除了多天线、多Packets外，增多可利用的子载波数量也是重要途径之一[5].此外，为直观表现重构效果，本文单独对60%测量值的LFMs626执行了逐值比较，见图8.

最后，本文对场景下基于MC 的方案进行了横向评测.对比的算法为常用的空间插值法：Kriging 法和反距离加权法（inverse distance weighted,IDW）[18]，选取的目标矩阵为LFMs410、LFMd401和LFMs616，评价标尺为TRE，结果见图9.

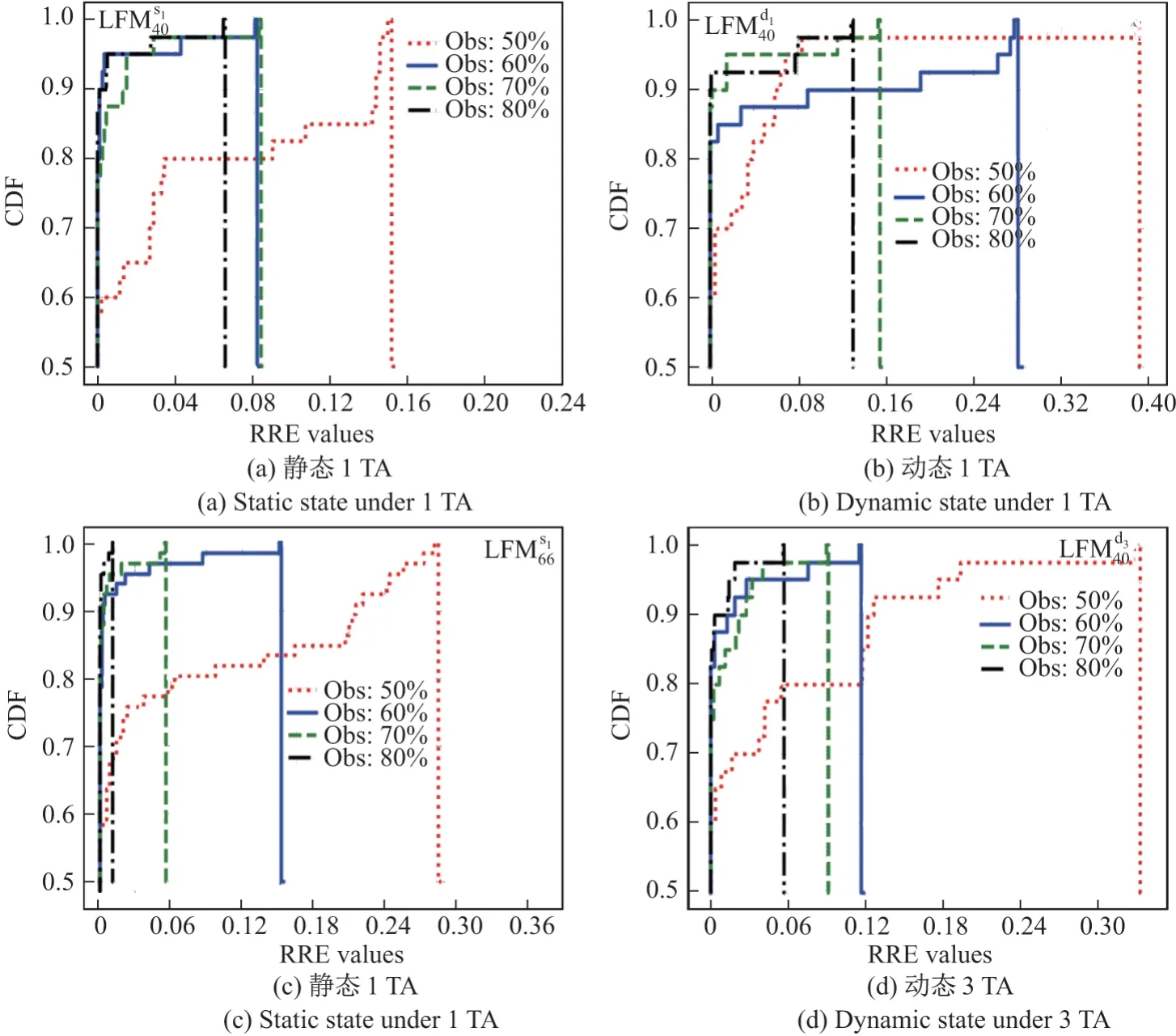
图7 不同条件下RRE 的累积分布函数Figure7 Cumulative distribution function (CDF) of RRE under different conditions

由图9可知：1）针对静态场景，在70%测量值下，当LFM 较小（LFMs140）时，3 种方法效果相当；LFM 较大（LFMs166）时，MC 精度高于IDW 且与Kriging 相当；针对动态指纹库的补全，MC 精度最优.2）观察值占比仍然是决定重构精度的重要因素，在较大静态场景，3 种方法对指纹库的恢复精度均随测量值的增加而提高.分析原因在于：IDW 算法结构简单，依靠局部估算值与测量值之间距离权重的平均进行重构，但抗噪声能力弱，拟合效果不佳；Kriging根据测量值的分布与相关度，进行差异化权重分配，且加入了误差预判机制，提高了估计准确度.但是其未考虑全局信息，选取的变差函数无法保证参数最优，从而使重构精度遇到瓶颈；基于MC 的算法依靠大量的迭代实现信息的通盘考量，取得了最好的效果，但相较插值法其时间开销较大.鉴于指纹库的重构是离线操作，因而在性能的取舍上，本文推荐精度的优先权应大于时间开销.

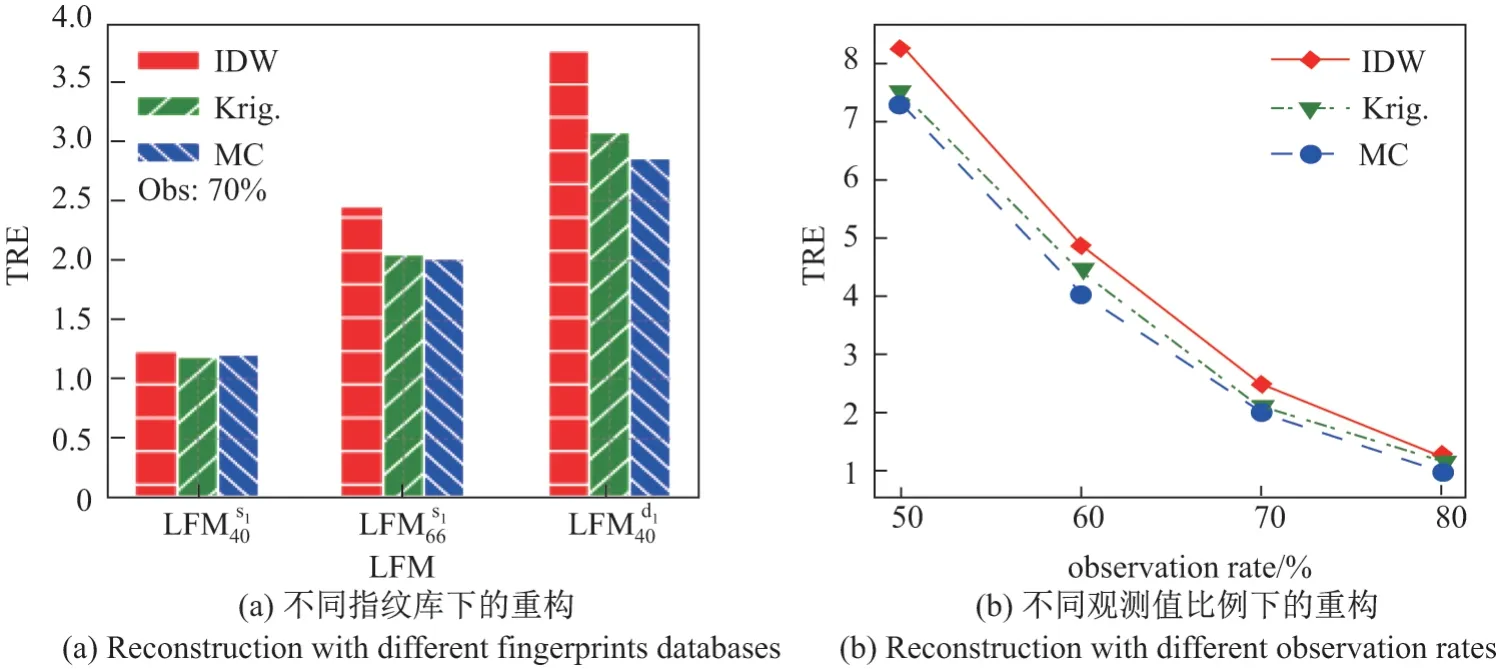
图9 不同重构方法对比Figure9 Comparison of different LFM reconstruction methods

5.3 定位性能评测

基于实测指纹库和重构库，以及所提的在线指纹匹配方法，本环节评测了系统的定位性能.鉴于FIFS[10]充分考虑了CSI 的频、空分集特性，指纹生成与匹配策略与本文相似，且取得了较优结果，因而选取它作为对比目标.评测方案见表2，各指纹库下的方案均完整执行4轮次，用于比对的数据源相同.结果见图10.

表2 定位评测方案Table2 Localization evaluation scheme

图10展示了可移动LRT 基于实测库的定位结果.在图10(a)中，相同颜色的数据点代表同一指纹库下的执行结果，不同的轮次用不同形状表征；图10(b)反映了所提系统的定位性能，其无误匹配均超过70%，最优的LFMs140下的比例超过了76%.静态实测库下1 m 内误差占比超过了80%，其中小场景下达到了85%；动态库下的表现相对较差，如图10(a)所示，稳定性较差，但在多TA 模式下，定位性能得到了改善，原因与5.2 节分析相同.需要注意的是，多TA 模式丢包率较高，经本文的现场测试，如果延长停留采集时间或优化采集手段，定位的性能会进一步得到提升.

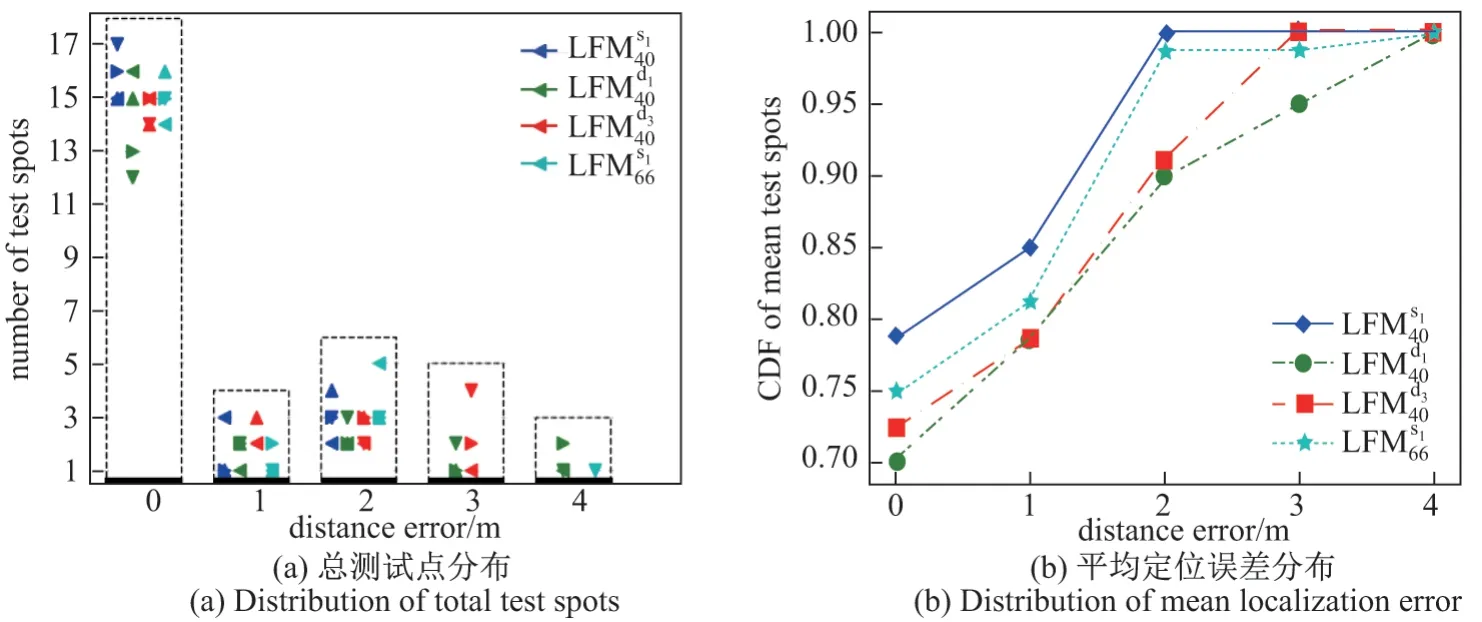
图10 不同实测指纹库下的定位误差Figure10 Localization errors with different actual fingerprints databases

基于上述采集的数据，我们按照表2在重构库下进行了综合定位评测，并选取两种静态库与FIFS 进行了比对.对于得到的4 轮次、每轮次20 个测试点的结果，采用平均定位误差作为评价标尺，结果见图11.

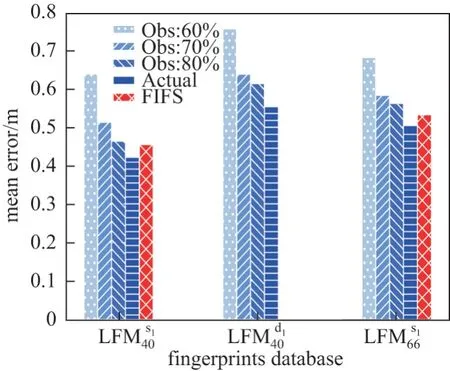
图11 平均定位误差对比Figure11 Comparisons of mean localization error

从图11可以看出，重构库下的定位性能同样正比于测量值.对于静态库下的两种场景，在60%测量值占比得到的重构库下，定位的平均误差最大，而70%占比与80%占比性能相当；70%重构库所取得的结果与实测库相比，误差均小于0.1 m.动态库下的定位误差高于同场景下的静态库，原因与位置指纹的不稳定有关.考虑到不同场景下LBS 的差异化需求，具体实施定位方案时，可以在效率与精度之间寻求一个折衷.如在本文的场景下，构建指纹库时可选择70%的测量值占比.

对于所提方案与FIFS 定位性能的比较，在图11两种静态场景下，所提系统基于实际库的误差均小于FIFS 方法；在80%占比的重构库下，系统的性能与FIFS 相当.所提系统占优的主要原因在于：1）设计了更稳定的位置指纹；2）更充分地利用了CSI 的频率和空间分集.此外，需要指出的是，场景的增大会减小两种方法的差距.

根据文献[7]所得的结论，指纹技术精度对采样点的尺寸有较高相关度.因此，为评估采样点缩小（精度分辨率提高）对所提方案的影响，本文对教研室场景进行了定位区域再划分，将采样点间隔D缩小为0.6 m，相应的指纹库规模扩大为8×12，并在静态场景下依靠742 N和841 N 得到两种实测库：LFMs196和LFMs296.随后进行了基于重构库的性能评测，其中重构环节设置测量值占比为70%.评测进行4 轮次、每轮次30 个随机测试点.由于采样点间隔较小，评测以估算LRT 所处位置的平均正确率分布为标准，结果见图12.

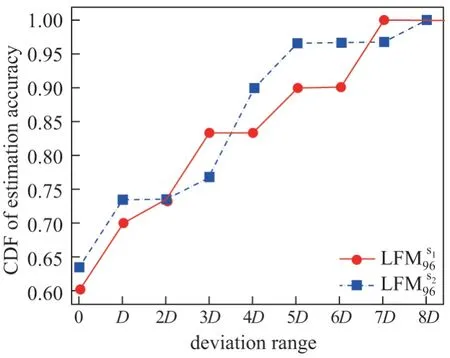
图12 位置估算的正确率分布Figure12 CDF of location estimation accuracy

图12中，横轴表示LRT 估计值与真实位置的偏差，如“2D”代表估计位置偏离实际位置2 个采样点（约1.2 m）.以图10(b)为对比，可以看出缩小采样点尺度反而会增大定位的偏差，如无误差的比例由约75%降为60%.其原因为：密集的采样会造成近邻CSI 指纹之间的区分度降低.尽管此举会给LFM 的重构带来误差减小，然而在匹配阶段，由于矩阵元素间有更强的相似度，造成所采用的基于概率匹配的估算方法性能降低.对于指纹技术，虽然缩小采样点的尺度是提供更精准LBS 的一个途径，但是根据本文的评测结果，如果不仔细设计匹配算法，反而会使定位性能有所下降.如保持匹配算法复杂度不变，则避免性能下降的手段可选择：1）利用多天线来稳定CSI 的波动.如图12中，双天线矩阵LFMs296具有较优的结果；2）利用数量更多的子载波[5].

6 结 语

本文借助IEEE 802.11n 标准下包含多个子载波频域特性的CSI，设计了一种基于细粒度位置指纹的定位系统.首先，系统充分利用CSI 的空间和频率分集优势，通过小波动指纹设计和MC 理论，提出了一种稳定、高效的指纹库构建方案；其次，利用贝叶斯准则概率模型，实现了定位阶段的指纹匹配；最后，在两个真实场景下多角度评测了系统的性能，各类的实验数据支撑了本文的理论预判，展示了所提系统的高效性和精准性.然而，所提系统未对多AP 和更多CSI 载波场景进行评测，且更精细的指纹匹配算法如深度学习也未涉及，这将在进一步的研究中开展.