三维光声图像重建的交替方向加权算法

齐梦雨， 赵丽丽， 刘 欣， 严壮志

1.上海大学通信与信息工程学院，上海200444

2.上海大学上海生物医学工程研究所，上海200444

光声成像技术是一种新兴的生物医学成像技术，它的基础是光声效应.当生物组织被脉冲激光照射时，被照射区域因光能量的沉积而产生热膨胀，从而产生微弱的光声信号.通过分布在生物组织周围的超声探测器阵列，或者按照指定轨道运动的单个超声探测器[1]，即可探测并采集光声信号.利用采集到的光声信号，通过一定的重建算法反演出待成像组织的光吸收分布，进而得到该组织的光学特性.近年来，光声成像技术在生物医学的很多领域取得了显著的成果，例如与纳米传感器结合的光声成像技术[2-3]，生物分子的光声成像和功能成像[4]以及多模态成像方式联合的光声成像[5]等.

高分辨率的图像重建往往需要处于不同位置的超声探测器采集足够充分的光声信号.为了提高数据采集的速度并保证采集数据的完备性，不同位置的超声探测器进行数据采集时一般采用多角度并行采集的方式.在这样的条件下研究出很多重建算法[6]，其中以迭代法最为常见.大多数迭代重建算法采用的是正则化L2范数的方法，但这种方法会引起图像局部特征丢失，进而导致过平滑现象[7]的出现.图像含有的不连续分量（例如轮廓和边缘）越多，这种过平滑现象也就越明显.因此，为了获得高分辨率的重建结果，传统的迭代法要求测量数据具有较高的完备性，这就大大增加了数据采集及成像时间.如何缩短数据采集时间或者只利用较少测量数据便可重建出理想的光声图像，已成为光声成像技术面临的重要挑战之一.

近年来，压缩感知理论在高分辨率光声成像领域发展迅速.根据该理论，如果图像具有可压缩性或者稀疏性，则能够在低于奈奎斯特采样率的条件下，以较高的分辨率重建出该图像[8].由于稀疏重建的算法大多基于L1范数正则化，因此越来越多的L1正则化方法被应用于光声成像领域[9].与基于L2范数正则化的重建方法相比，基于L1范数正则化的重建方法会保留图像的更多细节，从而在测量数据不完备的情况下也可重建出分辨率较高的光声图像[10].其中，文献[11]提出了一种基于L1范数正则化的交替方向算法（alternating direction method,ADM），可以利用很少的测量数据重建出较高分辨率的光声图像.由于这种算法可以节省大量的数据采集时间，因此成像速度得到了很大的提高.然而，对于更少的测量数据和更为复杂的组织结构，这种算法依然存在着精度和分辨率不足的局限.

本文提出了一种改进的交替方向加权算法，可以进一步提高在欠采样情况下光声图像重建的质量.交替方向加权算法基于传统交替方向算法，在迭代过程中引入了结构先验信息进行约束，显著抑制了伪影并降低了噪声，引导迭代计算过程中的原始变量和对偶变量向正确解收敛.实验结果显示，在采集数据较少的情况下，利用本文算法重建出的三维光声图像具有更好的精度和更高的空间分辨率.

1 三维光声图像的重建算法

1.1 光声成像的前向模型

根据光声效应原理，目标组织经过脉冲激光照射产生光声波并形成声场.在均匀和非粘滞的声介质中，光声波的传播公式为

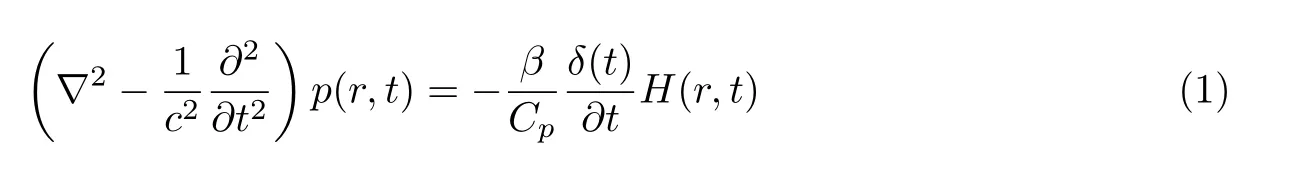
式中，c为声速，p(r,t)和H(r,t)分别描述的是位置r处、t时刻的声压和由于激光照射而产生的热能量沉积，Cp为等压比热容，β为等压膨胀系数.

如果满足如下热学限制条件和压力限制条件：1）脉冲激光持续时间小于组织的热扩散时间；2）脉冲激光的脉宽小于声波在目标组织中传播所需的时间，则热能量沉积函数H(r,t)就可以写成光源的时间包络函数与光能量沉积分布的乘积，即

式中，I(r,t)为光源能量的时间包络函数，µa(r)为位置r处的光吸收系数.如果将I(r,t)近似为冲激函数δ(t)，则根据式(1)求得位置r处、t时刻的瞬时声压为

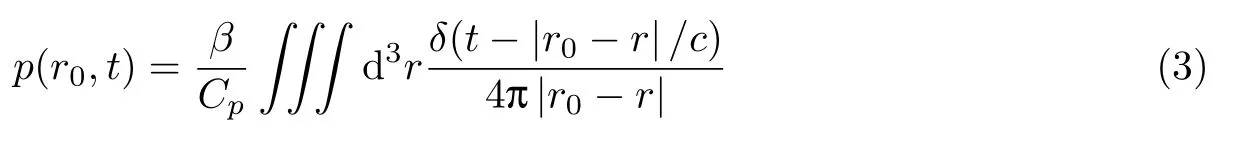
式(3)为光声信号的时域解析式.如果将介质进行离散，同时将超声探测器检测到的光声信号表示为向量b，那么基于式(3)，可以将光声成像的前向模型写成离散表达式[12]为

式中，W称为测量矩阵，可以理解为是光声信号在介质中的传播，而p0为t=0 时刻声场的初始值.

1.2 基于压缩感知的图像重建

一般而言，由于探测数据是不充分的，因此测量矩阵W是一个欠定矩阵.所以通过直接求解式(4)得到初始声压p0几乎是不可能的.光声图像在通过一定的变换后具有可压缩性或者稀疏性[7,13]，根据压缩感知理论，光声图像可以通过较少的探测数据进行重建.对于这样的一种稀疏变换ψ:x=ψp0，求解初始声压p0可以转化为最小化问题

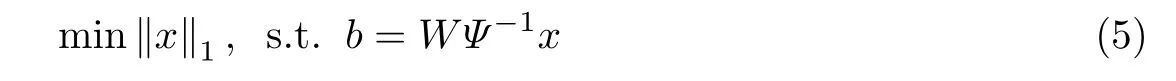
在这种情况下，式(5)中的限制条件也发生了变化

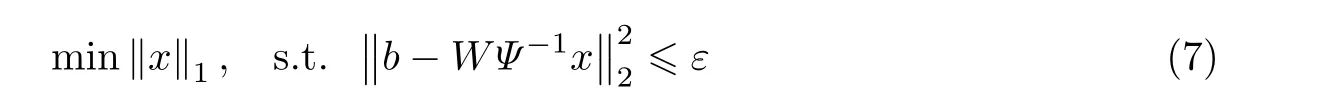
求解式(7)的问题可以转化为求解以下问题的最优解：

式中，σ是正则化参数.当σ和ε都接近于0 时，式(7)和(8)将会趋近于式(5).

1.3 传统交替方向算法

从数学的角度上，传统的交替方向算法[14]在对L1范数问题进行求解时，使用原始对偶算法（primal-dual algorithms）在每次迭代的过程中对原始变量和对偶变量同时进行更新.式(8)的增广拉格朗日子问题有如下形式：

式中，y为拉格朗日乘子，β(β ＞0)是惩罚项.如果已知，那么通过式(9)就可以求得对于r来说，如果给定x=xk且y=yk，式(9)取得最小值时满足

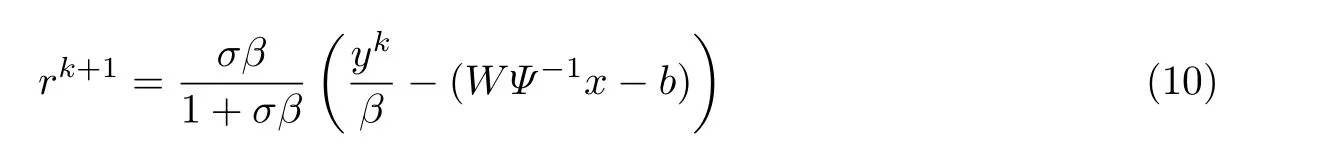
如果给定r=rk+1且y=yk，最小化式(10)相当于求解以下问题

通过对式(11)的求解[15]就可以得到

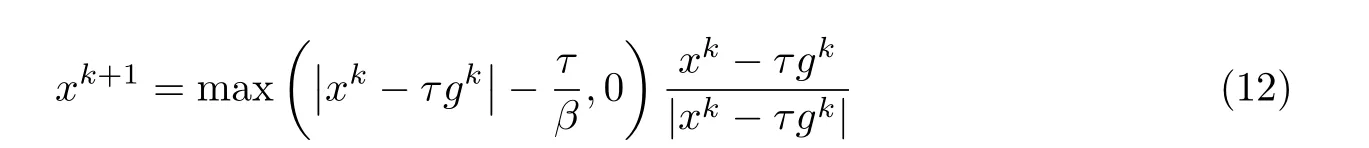
式中，τ(τ ＞0)是近似参数，并且有

最后，在已知r=rk+1和x=xk+1的情况下，下一次迭代中的乘子进行更新

在迭代过程中不断更新这些原始变量和对偶变量，在一定迭代次数后就可以得到最终解.

2 改进的交替方向加权算法

虽然基于L1范数正则化的传统交替方向算法在图像重建的过程中保留了图像的更多细节，但是在探测器数目不足和测量数据较少的情况下，传统交替方向法的重建图像依然存在着比较严重的伪影.如何进一步消除这些伪影，继续提升重建图像的分辨率和准确度是本文的主要关注点.由式(10)、(12)和(14)可知，在传统交替方向法的迭代过程中，原始变量和对偶变量会不断进行更新并最终得到最优解.如果某次迭代过程中的原始变量和对偶变量陷入了局部最优解，就会使图像在某些位置上产生噪点.由于测量数据较少和噪声干扰等原因，下一次迭代可能无法对这些噪点进行有效纠正，从而一定程度上导致了重建结果中部分伪影的产生.如果能够利用目标物的结构、形状或大致位置等先验信息对传统交替方向法的迭代过程进行约束，对于那些出现在反常位置上且大概率为噪点的值，在下一次迭代过程中进行适当的抑制，将有助于抑制伪影从而提高重建图像分辨率.

2.1 结构先验信息

交替方向加权算法通过引入先验结构信息来改善传统交替方向算法的迭代过程，使迭代结果向正确的结果快速收敛.在光声成像中，光声信号或图像由于自身的结构或者组成成分，往往包含天然的分组或分块先验信息.在交替方向加权法中，结构先验信息包含了目标组织的大致位置或形状等信息，具体呈现形式为三维权重矩阵Wi

式中，Ti为权重矩阵中目标组织大概率出现的位置，n为图像离散后的网格数目，a和b为权重值，且a ＞1,0＜b≤1.某点处对应的权重值大小代表了算法在迭代过程中对该点实际值的抑制程度，当权重值大于1 表示该点的实际值在迭代过程中趋向于被抑制，值越大代表被抑制的程度越大；当权重值小于1 表示该点的实际值在迭代过程中趋向于被增强，值越小代表被增强的程度越大；当权重值等于1 时表示该点的实际值维持原状态，既不被增强也不被抑制.由此可知，权重值a和b的大小实际上控制着迭代过程的速度和算法的收敛步长.在实际应用中，往往会根据待成像组织的天然结构、解剖特征，或者借助于其他成像技术来确定Ti的大致位置.例如文献[16]在脑部成像时借助于脑部的解剖结构以及不同部位的活跃程度对脑部进行了分组并确定Ti的位置，而文献[17]在荧光断层成像的研究中利用结构成像技术来获得Ti的大致位置.a和b具体数值将作为算法的输入参数加入算法的迭代过程中.本文在Ti位置处设置b=1，其他位置处设置a=10.

2.2 基于结构先验的交替方向加权算法

本算法中的结构先验信息以三维权重矩阵W′i的形式并作为式(8)的一个约束条件，加入到每一次L1范数正则化的过程中.这个约束条件可以描述为

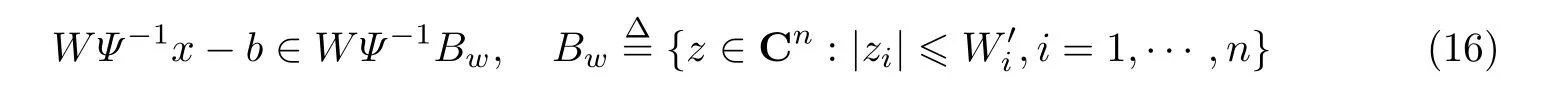
具体来说，加入结构先验信息后式(8)将具有以下形式：

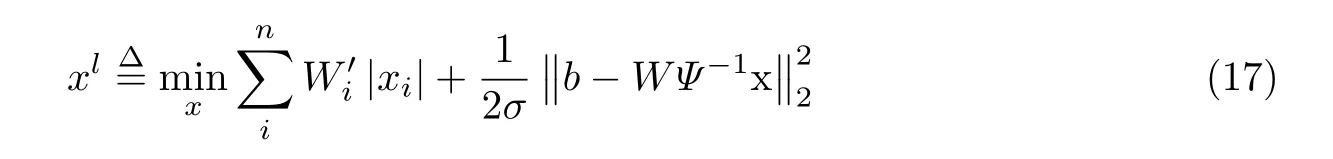
对式(17)的求解过程也就是利用传统交替方向法求解的过程.该式将作为算法外循环过程中的一次迭代，第l次外循环的结果将和结构先验信息一起作为第l+1 次外循环的迭代约束条件：

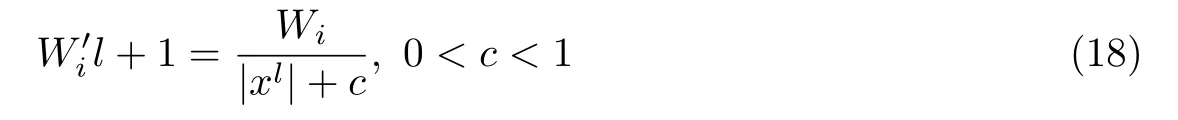
通过合理设置循环迭代容差来确定交替方向加权算法的终止条件，其中，内循环迭代容差为tol1，外循环迭代容差为tol2，且tol1与tol2决定算法的总迭代次数.

2.3 本文算法主要步骤

本文算法的主要步骤如下：

输入测量矩阵W和测量数据b，内循环和外循环终止条件tol1=e-4tol2=e-3.

输出初始声压分布的ψ稀疏逼近x.

初始化x=0，设置权重矩阵W′i=Wi，内循环迭代次数k=1，外循环迭代次数l=1.

步骤1使用原始对偶算法计算式(17)，并通过式(10)、(12)和(14)更新原始变量和对偶变量r,x,y.

步骤2如果满足返回步骤1 继续进行内循环迭代；否则，令xl=xk，并继续执行步骤3.

步骤3令

步骤4对式(17)加入结构先验约束，更新权重矩阵，即令

步骤5如果满足返回步骤1；否则外循环结束，输出xl.

3 实验结果与讨论

为了说明交替方向加权算法在欠采样条件下进行光声图像重建的优越性，本文进行了仿真实验，将分别使用最小平方QR（least squares QR，LSQR）算法、传统交替方向算法和本文提出的交替方向加权算法进行光声图像的重建.其中，LSQR 算法是基于L2范数正则化进行迭代重建，是一种求解大型线性方程组的经典方法.为了全面验证算法性能，将通过两个不同的方面进行仿真实验：1）在欠采样重建实验中，通过减少探测器数目并利用更少的测量数据进行重建，以验证本文算法在欠采样条件下进行三维光声图像重建的优势；2）在噪声鲁棒性实验中，对测量数据加入不同强度的噪声后进行重建，通过重建结果的比较来考察本文算法的噪声鲁棒性.仿真实验中的三维权重矩阵根据仿体的解剖学结构进行构建.探测器都按照理想的超声探测器进行处理.所有的仿真实验在MATLAB 平台上进行，光声信号的传播和声场的仿真使用了开源工具箱k-Wave[18].

3.1 欠采样条件下的光声图像重建

首先建立如图1(a)所示的仿体几何模型，仿体分为3 个部分，其中外部的大圆柱体为组织介质，内部大小相同且一上一下放置的两个小圆柱体为1 号和2 号目标物.组织介质的底面直径和高均为30 mm，总体积为15×15×30π mm3；内部的两个目标物体的底面直径和高分别为6 mm 和4 mm，体积均为3×3×4π mm3.介质和目标物的光吸收系数大小分别设置为Φ1= 1.0 mJ/mm3和Φ2= 5.0 mJ/mm3.48 个高斯光源均匀分布在以大圆柱体中心为球心、直径为45 mm 的球体表面.光源点和光扩散的过程通过有限元方法进行仿真.有限元模型总共有1 834 个格点和8 249 个正四面体网格.在声场的仿真和图像的重建过程中，仿体则被离散总数为27 000 的均匀网格.整个仿体声速均匀，声速大小设置为1 500 m/s.

图1 仿体模型与探测器阵列(单位:mm)Figure1 Geometry of phantom and position of the transducers (unit:mm)

首先利用24 个探测器的测量数据进行3 种重建算法的重建，将这24 个探测器每6 个为一组分为4 组，每组均匀分布在仿体z=3 mm，z=11 mm，z=19 mm，z=27 mm 4 个平面的圆柱体表面，如图1(b)所示.为了便于比较，图2中选取了重建结果中纵向通过1 号和2号两个目标物的y= 15 mm 平面.从图2(b)～(d)的重建结果中可以看到，LSQR、传统交替方向法以及本文算法都较清晰地重建出了两个目标物.这说明3 种算法在测量数据较完备的情况下都能取得较为理想的重建结果.但相比之下，LSQR 算法的伪影更为严重.此外作为一种L2正则化的重建算法，LSQR算法重建出的两个目标物由于算法产生的过平滑现象而导致边缘较模糊.图2(c)中基于L1正则化的交替方向法则保留了图像更多的细节，两个目标物的边缘更加清晰且呈现为两个大小相同的亮团.在图2(d)中，本文算法除了重建出两个大小一致的亮团外，背景噪声和伪影被大幅地抑制也使重建结果具有更好的空间分辨率.这体现出了结构先验信息在迭代过程中对于背景部分的约束作用，两个目标之间的背景部分根据结构先验信息而设置了较小的权重，所以在迭代过程中这些部分产生的伪影和噪声会被不断削弱.

为了比较3 种算法在欠采样条件下的重建结果，将每层的6 个探测器减少至2 个，同样分布在z= 3 mm，z= 11 mm，z= 19 mm，z= 27 mm 4 个平面上，如图1(c)所示.相比于使用24 个探测器，8 个探测器不仅在采集数据的数据量上较小，而且由于只在8 个位置处进行采集，所包含的位置信息也更少.这种条件下使用3 种重建算法得到的结果如图3(b)～(d)所示.从图中可知，3 种算法的重建结果都出现了不同程度的恶化.对比图2(a)和图3(a)可知，从LSQR 算法的重建结果中只能分辨出下方的1 号目标物，上方的2 号目标物则被严重的伪影干扰而无法分辨.LSQR 算法的过平滑现象由于欠采样而加剧，导致了很多图像细节的丢失.这一点在基于L1正则化的传统交替方向法中得到了一定程度的优化.从图3(c)可知，传统交替方向法得到的重建结果虽然也存在着比较严重的伪影，但是上方2 号目标物的部分细节仍然被保存了下来.相比之下，本文算法的重建结果虽然由于欠采样仍然产生了一定的伪影和噪点，但是两个目标物的位置准确，大小也基本一致.由于结构先验信息的约束，三维权重矩阵中权重值较大位置处的伪影在迭代过程中持续被抑制，在重建结果上体现为背景噪声很小，分辨率更优.

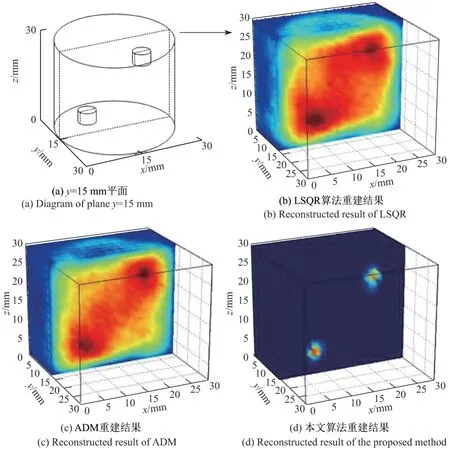
图2 使用24 探测器进行不同算法的重建结果对比(y =15 mm)Figure2 Comparison of reconstructed image with 24 sensors from different method (y =15 mm)

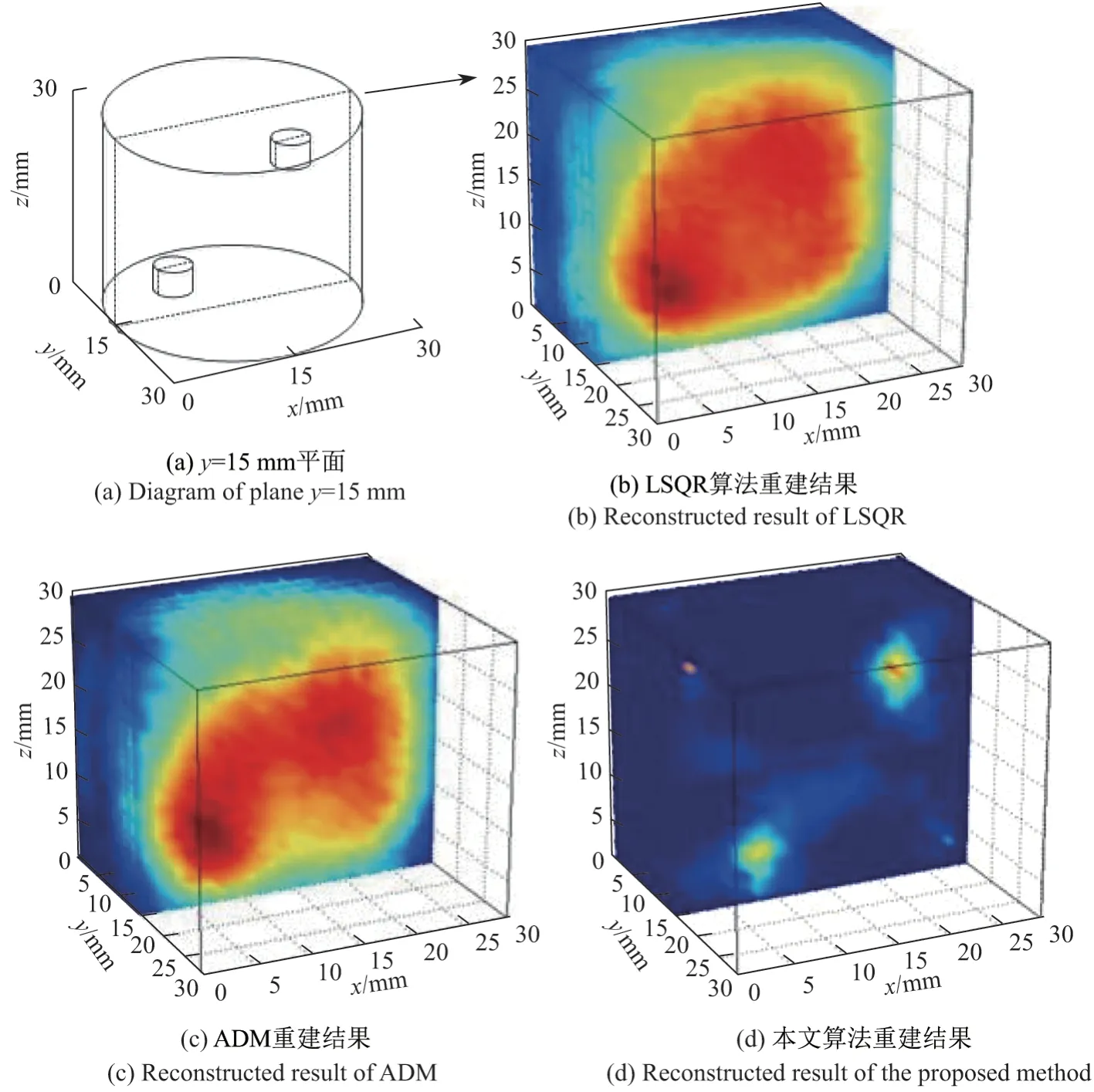
图3 使用8 探测器进行不同算法的重建结果对比(y =15 mm)Figure3 Comparison of reconstructed image with 8 sensors from different method (y =15 mm)

对于使用8 个探测器的欠采样条件下的重建结果，除了选取图3中的y=15 mm 截面外，在图4和5 的重建结果中还选取了通过目标物中心的z= 6 mm 和z= 24 mm 两个平面进行展示.对比图4(b)～(d)可知，在z= 6 mm 平面上，使用LSQR 算法得到的重建结果水平分辨率最差且伪影严重，图4(c)中使用传统交替方向算法得到的重建结果则对伪影有了一定程度的削弱.而在图4(d)中，使用本文算法得到的重建结果在z=6 mm 平面上有效地抑制了伪影，水平分辨率有了显著提升.z= 24 mm 平面的重建结果与z= 6 mm类似，本文算法的重建结果有效抑制了伪影，因此水平分辨率相较于LSQR 和传统交替方向法有明显提升，如图5(d)所示.对比图4(b)、图5(b)以及图4(c)、图5(c)，无论是使用LSQR 算法还是使用传统交替方向法，其重建结果在两个平面上的水平分辨率都存在着差别，且在z=6 mm 平面上的水平分辨率都明显优于各自在z=24 mm 平面的水平分辨率.此外，LSQR 算法和传统交替方向法在这两个平面上重建出的目标物也存在着大小和形状上的差异.相比之下，本文算法的重建结果在两个平面上不仅拥有相似的水平分辨率，而且能够重建出大小基本一致的目标物，这也体现了本文算法在欠采样条件下的稳定性.

为了进一步衡量不同算法的重建性能，通过将不同算法的重建图像归一化后，与两个目标物所在的真实位置相比，得到了不同算法的均方误差（mean square error,MSE）和峰值信噪比（peak signal to noise radio,PSNR），如表1所示.

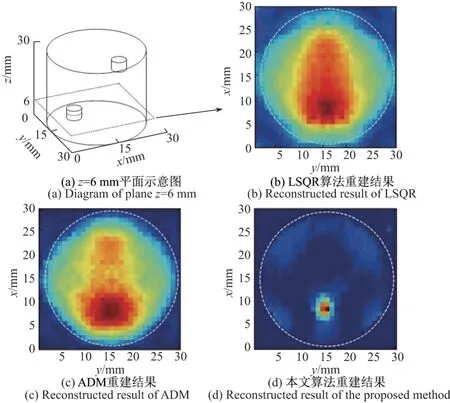
图4 不同算法重建结果的水平分辨率对比(z =6 mm)Figure4 Horizontal resolution comparison of reconstructed image by different method(z =6 mm)

图5 不同算法重建结果的水平分辨率对比(z =24 mm)Figure5 Horizontal resolution comparison of reconstructed image by different method(z =24 mm)

表1 3 种重建算法的性能比较Table1 Performance comparison by three reconstruction algorithms

从表1中可知，在y= 15 mm 平面上，与LSQR 算法相比，虽然传统交替方向法的结果MSE 较低而PSNR 较高，不过这种差别并不明显.反观本文算法的重建结果，MSE 值明显下降（约为90）而PSNR 值出现了较大程度的上升（约为4 dB），说明本文算法的重建结果有着最优的垂直分辨率.在z=6 mm 平面上，传统交替方向法的MSE 值与LSQR 算法相比有了一定程度的下降（均为32 左右），同时PSNR 提升了约1 dB，说明传统交替方向法的重建图像质量方面要略优于LSQR 算法.本文算法由于在传统交替方向法基础上通过结构先验信息进行进一步优化，所以MSE 值出现了明显下降而PSNR 值出现了明显的上升（约为6 dB），这充分证明了本文算法对于2 号目标物的重建结果，在水平分辨率上比前两种方法有了大幅提升.此外，传统交替方向法在z=24 mm 平面上的PSNR 值反而略低于LSQR 算法，说明传统交替方向法的重建结果在水平分辨率上并不稳定，而本文算法的重建结果在z= 24 mm平面上依旧有着最低的MSE 和最高的PSNR，充分说明了本文算法的稳定性.

综上，在欠采样的条件下，LSQR 方法和传统交替方向法重建出的目标物在位置和大小上都存在着或多或少的偏差，而本文算法则在正确的位置上重建出了两个大小相同的目标物，和预期结果相符.此外在这3 种算法中，使用本文算法重建出的结果在多个平面上都具有最小的MSE值和最大的PSNR 值，同时具有最好的垂直和水平分辨率.图2～4 的(b)和(c)中目标物周围的大面积伪影在图2～4 的(d)中基本消失，亮团准确地定位在两个目标物的真实位置处，这也造成了视觉上的较大差异，充分表明本文算法中引入的结构先验信息起到的纠正目标物位置，抑制伪影和提高重建结果分辨率的作用.

3.2 噪声的鲁棒性实验

算法良好的噪声鲁棒性在其实际应用中具有很大意义.为了研究噪声对不同算法重建结果的影响，分别在测量数据中加入不同强度的高斯噪声，其作用是模拟真实实验中的系统噪声.本实验的参数和设置与前述相同，测量数据是使用24 个探测器采集得到.三维光声图像的重建过程分别在信噪比（signal to noise radio,SNR）为80 dB 和120 dB 的条件下进行，其中信噪比越小，说明加入噪声的强度越大；反之信噪比越大，则说明加入的噪声强度越小.3种算法在不同噪声条件下的重建结果如图6～8 所示.

图6 不同噪声条件下LSQR 算法的重建结果Figure6 Reconstructed image using LSQR method under different noise conditions

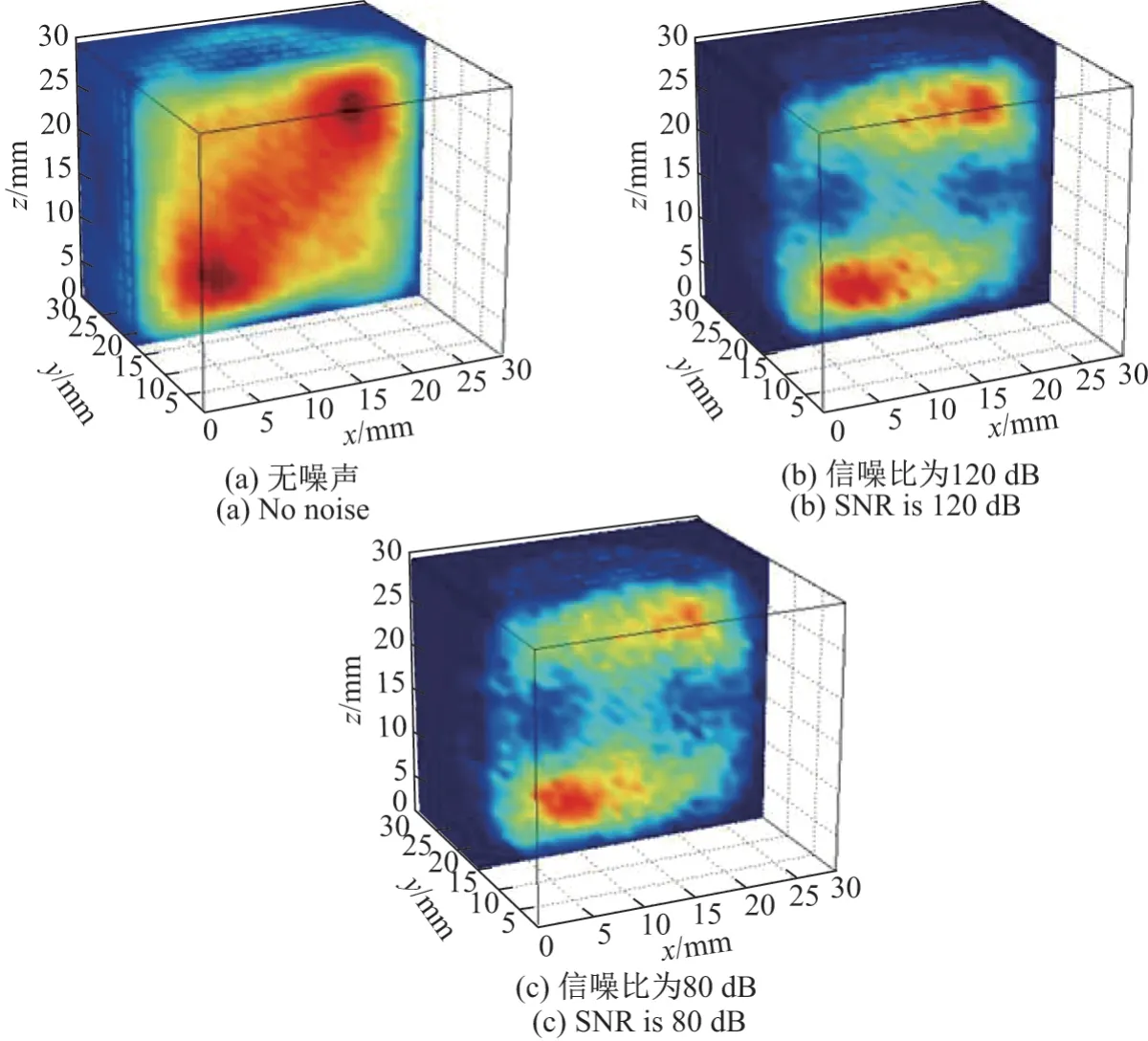
图7 不同噪声条件下ADM 算法的重建结果Figure7 Reconstructed image using ADM under different noise conditions

从重建结果中可以看到，随着SNR 逐渐变小，3 种算法在图像的分辨率上都出现了不同程度的下降.根据图6(a)～(c)可知，随着噪声的增加LSQR 算法重建结果中的伪影迅速增多，在SNR= 120 dB 时噪点和伪影已经严重影响了目标物的分辨率，而在SNR= 80 dB 的条件下，两个目标物都由于伪影和噪点的影响已经不再呈现团状.而在图7(b)和(c)中，虽然随着SNR 的不断减小，传统交替方向法重建出的目标物附近出现了较严重的伪影以及拖尾，但依旧保持了目标物的大致形状和位置信息，这里再次体现出了基于L1正则化方法在保留图像细节和边缘方面的优势.在使用了本文重建算法的图8(b)和(c)中，由于加入噪声的缘故，两个目标物在相对的方向上均出现了一定的伪影，尤其当信噪比下降至80 dB 时这种现象更加明显，但是相比图6(c)和图7(c)而言，仍能够明显分辨出两个目标物的位置和大小.在本文算法的迭代过程中，包含着结构先验信息的权重矩阵在远离目标物的位置处具有较大的权值，所以这些部位产生的噪声在多次迭代后逐渐被抑制甚至消除，这也是图8(c)中伪影主要集中在两个目标物附近以及两个目标物的中间部位、而在远离目标物的位置十分微弱的原因.从图6(c)、图7(c)以及图8(c)的对比中看到，这些产生在目标物及其附近位置处的伪影一般不会导致分辨率急剧恶化.综上，相比LSQR 和传统交替方向法，本文算法在不同的噪声条件下都可以得到分辨率较高的重建结果，因此对于噪声具有较好的鲁棒性.

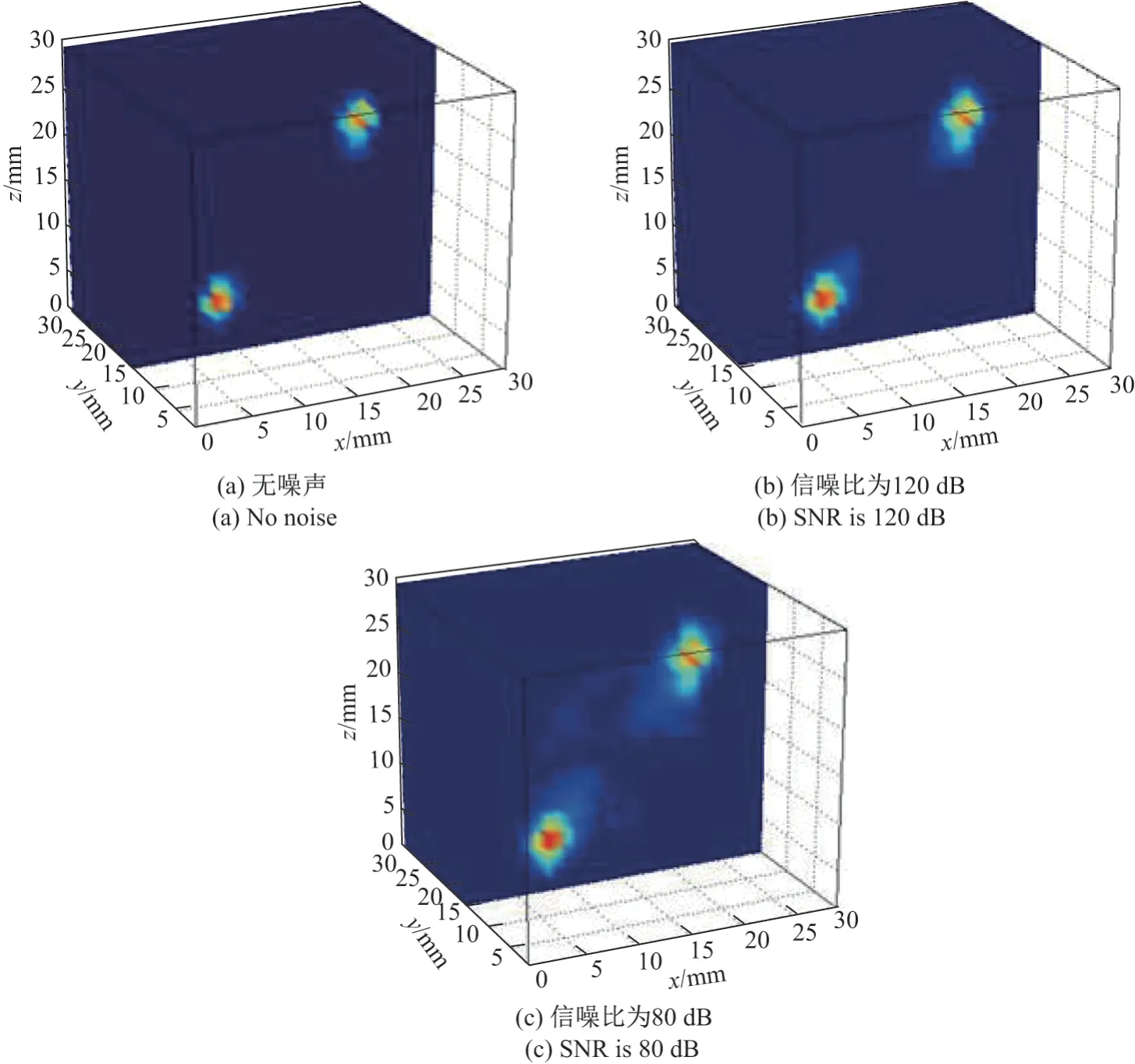
图8 本文算法在不同噪声条件下的重建结果Figure8 Reconstructed image using proposed method under different noise conditions

4 结 语

光声成像是一种融合了超声成像和纯光学成像的多模态成像技术，兼具高成像深度和高对比度的特点，应用场景多样，因此具有光明的发展前景.然而，在成为一项成熟的且可普遍用于临床的成像技术之前，光声成像仍面临诸多挑战.其中最主要的就是因数据采集量较大导致的数据采集时间过长以及较苛刻的硬件要求.为此，本文提出了一种L1范数正则化的交替方向加权算法.该算法对传统交替方向算法进行了改进，通过设计仿真实验对比了不同算法在欠采样条件和噪声条件下的重建结果，验证了本文算法的优势.实验结果证明，交替方向加权算法可以利用较少的测量数据重建出分辨率和精度都较高的光声图像，同时也具有较好的噪声鲁棒性.这对于减少光声成像在实际应用中的数据采集时间，提高成像速度具有积极意义.下一步工作将考虑本文算法在真实实验中的应用，并对本文算法的性能和应用场景等进行更深入的研究.