基于推广流形学习的高分辨遥感影像目标分类

郭亚宁 林伟 潘泉 赵春晖 胡劲文 马娟娟

随着计算机、空间定位、航空航天以及传感器技术的不断发展,对地观测系统的光谱和频谱分辨率不断增加,时间和空间分辨率不断提高,现代遥感技术已经形成高光谱、高空间分辨率、全天时/全天候、实时/准时的对地观测能力,可以采集到分米甚至纳米级的高分辨率遥感影像[1].众所周知,高分辨率遥感影像不仅在现代军事战争中承担及时、准确获取军事信息的重大任务,在城市规划、灾害监测与评估等民用领域也具有广泛应用[2].然而,高分辨遥感影像解译技术远远滞后于影像的获取技术,使其在现实应用中并未得到充分利用.大量的理论分析与实验结果表明,高分辨率遥感影像数据在带来强烈视觉冲击的同时,也带来了一系列信息处理与模式识别的新问题,影像空间分辨率的提高并不意味着解译精度也一定提高[3].

如何对高分辨率遥感影像数据进行快速准确解译是目前亟待解决的一个难题.目标分类与识别是高分辨遥感影像解译的关键技术之一.目前,高分辨率遥感影像目标分类主要存在两个挑战[4]:1)目标的结构特征成为影像分类的主导因素[5];2)影像光谱特征的统计可分性减弱,类间方差[6]减小,类内方差变大,“同物异谱、同谱异物”的现象普遍存在.因此,适用于中低分辨率遥感影像的特征(例如强度特征、纹理特征等)及光谱解译方法并不适用于高分辨率遥感影像.

但是,如果将图像的重构信息和分类识别信息看作是嵌入在低维子空间中的一个流形,则既可以处理高维数据又可以挖掘数据内蕴几何结构特征的流形学习是解决上述问题的有效途径.近年来,流形学习被广泛用于行人检测[7]、视觉物体分类[8]、高光谱遥感图像分类[9]、人脸识别[10]、图像分类[11]等模式识别和数据分类问题,及动态目标追踪[12]、医学图像分割[13]、显著性检测[14]等计算机视觉和人工智能领域.

流形是不同维数下的曲线和曲面等几何对象的总称.流形学习本质是通过非线性映射将高维数据投影到低维空间,提取数据内蕴结构特征,实现维数约简或数据可视化.Tenenbaum等[15]和Roweis等[16]首先在非欧框架下考虑数据集的几何结构分析问题,在2000年的Science杂志上分别提出考虑全局几何结构的保测地距离映射(Isometric mapping,Isomap)和考虑局部几何结构的局部线性嵌入(Locally linear embedding,LLE).Isomap和LLE方法均可以把采样数据所在的低维流形展开成低维子空间.受Isomap和LLE启发,各种非线性维数约简算法大量涌现.具有代表性的方法主要包括:拉普拉斯特征映射(Laplacian eigenmap,LE)[17]、局部切空间排列(Local tangent space alignment,LTSA)[18]、最大方差展开(Maximum variance unfolding,MVD)[19]、黑塞局部线性嵌入(Hessian locally linear embedding,HLLE)[20]和局部坐标排列(Local coordinates alignment,LCA)[21]等.

但上述方法中的投影函数均是非线性的,即没有显式表达.因此,无法直接利用投影函数求出测试样本或新样本的低维投影,而需要将其加入训练样本重新训练算法,且每重新运行一次,就相当于摒弃了之前的运算结果,这将耗费大量的时间和计算量,在实际应用中并不可取.为此,He等[22]提出LE的线性化算法:局部保持投影(Locality preserving projection,LPP);Kokiopoulou等[23]和He等[24]提出了LLE的线性化算法:正交邻域保持投影(Orthogonal neighborhood preserving projection,ONPP)和邻域保持嵌入(Neighborhood preserving embedding,NPE).

虽然线性化方法很好地解决了新样本问题,但仍存在以下缺点:1)均是无监督学习方法,即没有利用样本类标信息,不利于分类识别问题;2)均是在欧几里得框架下基于数据特征向量化表示的降维算法,但实际应用中的数据并非全分布在欧氏空间内,例如对称正定(Symmetric positive define,SPD)矩阵,其所诱导的空间是非欧、弯曲的黎曼流形.作为一种典型的SPD矩阵,协方差描述子融合了图像多种特征,对目标大小、形状和光照变化等具有较强的鲁棒性,近年来被广泛应用于目标跟踪[10]、人脸识别[25]、行人检测[26]等方面.若对大小为n1×n2的协方差描述子进行降维处理,经典流形学习算法需要首先将其向量化为(n1×n2)×1的向量,然后利用欧氏距离进行相似性度量.但向量化表示通常会忽略数据各维度的变化,且易破坏数据内蕴几何结构.同时,利用欧氏距离度量黎曼流形上两点间的相似性会忽略数据特征的空间分布信息.此外,当数据维度较高时,将面临“维数灾难”和较大计算复杂度.因此,传统欧氏框架下的流形学习算法不能有效用于黎曼流形.

为此,本文结合黎曼流形理论与核方法,提出一种推广的流形学习算法,即基于Log-Euclidean黎曼核的自适应半监督正交局部保持投影(Log-Euclidean Riemannian kernel-based adaptive semi-supervised orthogonal locality preserving projection,LRK-ASOLPP)算法,并将其应用于高分辨率遥感影像目标分类研究.该方法是针对高分辨率遥感影像目标分类提出,但具有通用性,也适用于其他类图像的分类与识别研究.也可以通过类似的方法将流形学习算法ONPP从欧氏空间推广到黎曼流形上.与经典的流形学习算法相比,本文提出的LRK-ASOLPP算法在继承LPP优点的同时,具有如下优点:1)该算法成功地将传统的流形学习算法LPP推广到黎曼流形上,无需对协方差描述子进行向量化表示,就可将其投影成低维向量,在有效保持图像特性内蕴几何结构的同时,减少了计算量和存储空间;2)在核化的过程中,通过引用无参Log-Euclidean黎曼核,克服传统核方法中存在的核参数的选择问题;3)经典的流形学习通常在原始特征空间中构建近邻图,本文所提出的算法则充分利用数据特征在低维空间中空间分布与样本点的先验类标信息,在低维特征空间中构建近邻图来估计数据特征的内蕴几何结构,并通过交替迭代优化算法进行求解,同时获得相似性权矩阵与低维投影矩阵,以此提高算法性能.

本文内容安排如下:第1节简单介绍图像协方差描述子;第2节基于黎曼流形理论给出了黎曼流形上的Log-Euclidean黎曼核的定义;第3节重点阐述和分析了所提出的LRK-ASOLPP算法;第4节是高分辨率遥感影像目标分类的实验结果;最后总结全文.

1 协方差描述子

Tuzel等[27]首先提出用协方差矩阵作为图像区域特征描述子,即给定灰度或RGB图像I∈RW×H,记F=[f(x,y)]∈RW×H×d为图像I的特征张量,f(x,y)=φ(I,x,y)∈Rd表示像素点(x,y)处的特征向量.函数φ(I,xi,yi)=fi可以是灰度值、颜色、一阶和二阶(水平、垂直)差分、梯度模、梯度方向以及滤波响应等图像特征信息,(xi,yi)表示第i个像素点的位置.给定图像区域R⊂F,记表示区域R内每个像素点处的d维特征向量集,则区域R的d×d维协方差矩阵为

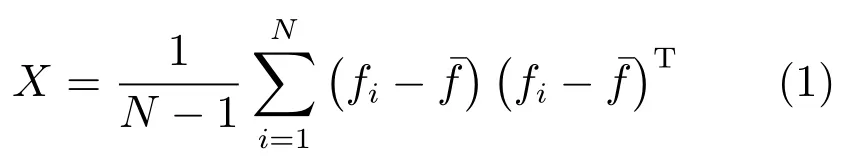
2 黎曼流形上的Log-Euclidean黎曼核

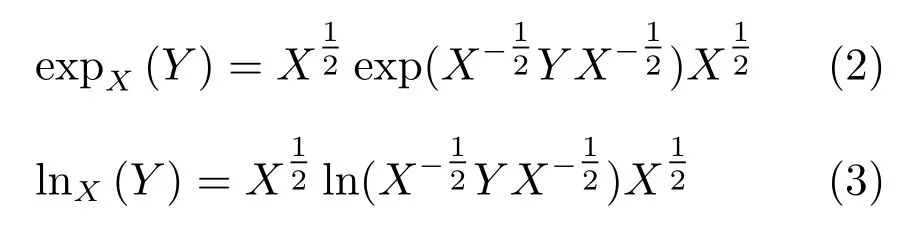
其中,exp(·),ln(·)分别为矩阵的指数算子和对数算子.对,根据奇异值分解(SVD),X可被分解为X=UΣUT,其中 Σ =diag{λ1,λ2,···,λd},λi,i=1,2,···,d为特征值,U为特征值所对应的特征向量所构成的矩阵.则

其中,

由式(5),(7),(9)可知,Log-Euclidean黎曼核无核参数,且充分利用了样本点的正定对称特性,简化了核矩阵的计算过程.

定理1.Log-Euclidean黎曼核满足Mercer条件.

证明.

1)kln实对称:kln(Xi,Xj)=kln(Xj,Xi)

因为

对∀A,B∈RN×N,tr[A·B]=tr[B·A],故

2)kln正定: 对,∀b1,b2,···,bN∈R

因此,本文在核化的过程中选用Log-Euclidean黎曼核,以克服传统核方法中存在核参数选择问题.

3 LRK-ASOLPP算法

算法原理:1)提取图像每个像素点处的几何结构特征,计算图像特征的协方差描述子;2)采用Log-Euclidean黎曼核将协方差描述子投影到再生核Hilbert空间;3)基于流形学习理论,建立黎曼流形上半监督正交局部保持投影算法模型,利用交替迭代更新算法对目标函数进行优化求解,获取相似性权矩阵和低维投影矩阵;4)利用所求得的低维投影矩阵计算测试样本的低维投影.

3.1 算法模型建立与优化求解

3.1.1 模型建立

定义非线性映射φ:M 7→F,将分布在黎曼流形M上的样本点Xi投影到再生核Hilbert空间F:

定义低维投影矩阵V:F 7→Rr,使得

1)构建相似性权矩阵

在低维空间中,利用k近邻法寻求每个低维特征Yi的k个最近邻点,记作,记为中与Yi异类的样本.定义相似性权矩阵.

2)构建黎曼流形上半监督正交局部保持投影算法模型

由于对∀V∈F都有V∈span{φ(X1),φ(X2),···,φ(XN)},即存在数组使得

将φ(Xi)投影到V上,有

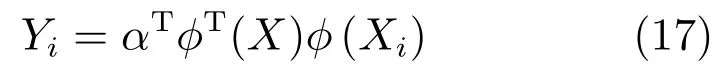
定义核矩阵K=(Kij)N×N,其中

记

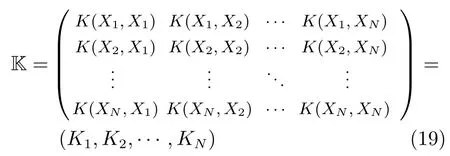
将式(16),(18)和(19)代入式(17),得

则由

得优化问题(15)的求解等价于求解

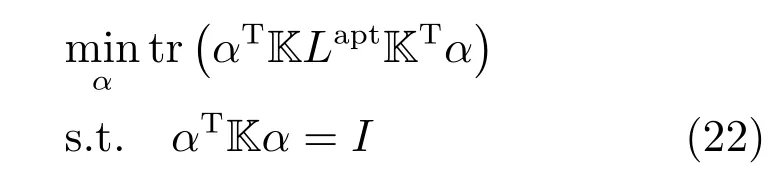
其中,Lapt是Laplacian矩阵,是度矩阵,.

由Rayleittz-Riz定理可知,上述优化问题的求解等价于求解如下广义特征问题:

其中,α=(α1,α2,···,αr)即为前r个 (除 0 之外)最小特征值λ1,λ2,···,λr对应的特征向量.

3.1.2 优化求解

由权矩阵Wapt的构造方法可知,Lapt由α决定,而由式(23)可知α由Lapt决定,因此优化问题(22)没有封闭解.为此,本文利用交替迭代优化算法对其进行求解. 首先,给定αt−1,求Lapt(αt−1),然后利用Lapt(αt−1)求αt,依次循环迭代,得到局部最优解.

则广义特征问题(23)修正为如下特征问题:

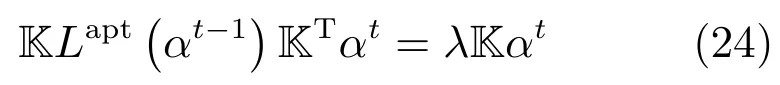
进一步,由式(20),训练样本的低维投影为

由于α∈RN×r,K∈RN×N,故Y∈Rr×N,即协方差描述子的低维投影是欧氏空间中r×1维向量.特别地,当迭代次数t=1时,LRK-ASOLPP算法是在数据原始特征空间中构建的近邻图,此时算法记为LRK-SOLPP.

3.2 算法描述与计算复杂性分析

3.2.1 算法描述

基于Log-Euclidean黎曼核的自适应半监督正交局部保持投影(LRK-ASOLPP)算法描述如下:

算法1.LRK-ASOLPP算法

输入.X={X1,X2,···,XN}⊂M,Xi∈Rd×d,为有标签集,是无标签集,N为训练样本的总个数,降维后的维数r,最大迭代次数T.

输出.α=(α1,α2,···,αr),r,Y=(Y1,Y2,···,YN).

3.2.2 计算复杂性分析

算法的时间复杂性主要包括计算Lapt和计算广义特征值.计算Lapt的时间复杂性为O(kN2),k是近邻个数,N是样本总数;计算广义特征问题(23)的时间复杂性为O((N+r)N2).因此,算法整体计算时间复杂性为O((N+r)N2).

3.3 新样本嵌入

对于测试样本或新样本Xt,其低维投影为

其中,

4 实验仿真

为验证LRK-ASOLPP算法的有效性,本文选用高分辨率遥感数据集UCMerced LandUse Dataset[29],WHU-RS Dataset[30]及Quick bird Dataset作为实验数据,从参数设置及其敏感性、低维特征可视化和分类精度三个方面对算法性能进行分析,并与基于Log-Euclidean高斯核局部保持投影(Log-Euclidean Gaussian kernel-based locality preserving projection,KLPP)算法[31]和LRKSOLPP算法进行对比.

4.1 数据集

1)UCMerced LandUse Dataset共包含21类地物,每类包含100张不同时间、地点、光照和拍摄角度等条件下,大小为256像素×256像素的影像.

2)WHU-RS Dataset包含19类地物,每类包含55张不同时间、地点、光照和拍摄角度等条件下,大小为600像素×600像素的影像.

3)Quick bird Dataset包含17类地物,每类包含80张不同时间、地点、光照和拍摄角度等条件下,大小为400像素×400像素的图像.

实验中,在每个数据集中,首先将每类图像平均分为5个子集,每次无放回随机选择3个子集作为训练样本,其余2个子集作为测试样本,将图像大小统一调整为64像素×64像素,并对像素值做归一化处理;其次,计算每张图像的每个像素点(x,y)处的特征向量f(x,y)=(x,y,HR(x,y),HG(x,y),HB(x,y))T,其中表示图像的一个通道,再根据式(1)计算协方差矩阵X,其中X为17×17的对称正定矩阵;然后,分别利用KLPP,LRK-SOLPP和LRK-ASOLPP算法将其投影到低维欧氏空间;最后,利用K-NN,K-means,SVM,BP-ANN等分类器进行分类.类似十折交叉验证法,实验重复10次,取分类精度平均值作为算法性能的评价指标.

4.2 参数设置及其敏感性分析

本文提出的LRK-ASOLPP算法涉及的参数有γ,ξ,ζ,k以及有标签训练样本的个数l'.其中,γ,ζ分别表示同类样本点和异类样本点之间的相似性权重,ξ表示k个近邻点中类别不确定的点之间的权重.实验中,取γ=−ζ=8,ξ=1;显然,有标签样本个数越多,分类精度就越高,本文实验中均取l'=3;设置最近邻参数k搜索范围为k={1,2,···,l−1},其中l为训练样本的个数.为验证算法LRK-SOLPP,KLPP及LRK-ASOLPP对最近邻参数k的敏感性,选用SVM作为分类器.最佳分类精度随k的变化曲线如图1所示.

由图1可知,在三个数据集上,当k≥12时,本文提出的LRK-ASOLPP算法趋于稳定,且当k分别取12,10,14时,分类精度最高,分别为0.9428,0.9645,0.9487.

4.3 低维特征可视化

以WHU-RS Dataset为例.首先从WHU-RS Dataset中任选4类地物,以机场、海岸线、桥梁和山脉为例,然后计算每个像素点处特征向量f(x,y)=(x,y,HR(x,y),HG(x,y),HB(x,y))T,其中,f(x,y)=(x,y,HR(x,y),HG(x,y),HB(x,y))T,其中,,h∈{R,G,B}表示图像的一个通道,再根据式(1)计算协方差矩阵X∈R17×17;最后,利用KLPP,LRKSOLPP和LRK-ASOLPP算法将其投影到三维空间,实验结果如图2所示.

由图2可知,使用KLPP投影后,类间存在交叉重叠,而使用本文提出的LRK-ASOLPP算法将高维特征投影到低维特征空间后,类内紧凑、类间分散,而且明显优于LRK-SOLPP.

4.4 图像分类仿真实验

本节从三个方面将本文提出的LRK-ASOLPP算法与LRK-SOLPP和KLPP算法进行比较,分析评价LRK-ASOLPP算法的性能.

1)基于特征维数r的分类精度

根据图1取k=12,在三个不同数据集上,对不同特征维数r,算法KLPP,LRK-SOLPP,LRKASOLPP分别结合SVM的分类效果如图3所示,各方法最佳分类精度及其对应特征维数见表1.

表1 最佳分类精度(Ac)及对应特征维数(r)Table 1 The classification accuracy(Ac)and the corresponding feature dimension(r)

图1 不同近邻数k对应的分类精度Fig.1 Classification accuracy for different values ofk

由图3及表1可知,LRK-ASOLPP算法分类效果最佳,且对比LRK-SOLPP与LRK-ASOLPP的实验结果可知,选用交替优化迭代求解方法可以明显提高算法的分类精度.

2)基于训练样本个数的分类精度

图2 三维特征可视化图Fig.2 3D feature visualization

对每个数据集,分别从每类图像中随机选择2,3,4个子集作为训练样本,其余子集作为测试样本,结合SVM的实验结果如图4所示.

由图4可知,训练样本个数对算法的性能有一定的影响,即随训练样本的增加,算法的分类精度提高,LRK-ASOLPP算法的分类精度最高,且明显优于LRK-SOLPP和KLPP算法.

3)基于不同分类器的分类精度

图3 最佳分类精度随特征维数变化曲线图Fig.3 The varying curves of the optimal classification accuracy with feature dimension

在三个数据集上,首先利用 LRK-SOLPP,KLPP及LRK-ASOLPP将测试样本的协方差描述子投影到低维空间;其次,利用不同的分类器(KNN,K-means,SVM,BP-ANN)进行分类.其中,对于K-NN和K-means,取k=15,对于SVM,选择线性核函数.实验结果如表2～4所示.

图4 三个数据集上不同训练样本数算法最佳平均分类精度Fig.4 The average classification accuracy of different training sample number on three datasets

由上述实验结果可知,分类器不同,算法的分类效果也不同.本文提出的LRK-ASOLPP算法结合K-NN,K-means及SVM时,分类效果均优于其他算法,且与BP-ANN结合时,分类精度最高.

5 结束语

传统的流形学习算法均是欧氏框架下基于图像特征向量化表示的降维算法,而协方差描述子所在的空间是非欧和弯曲的黎曼流形,对其进行向量化表示并用欧氏距离进行相似性度量容易丢失有效的结构信息.因此,本文结合黎曼流形理论与核方法,将流形学习算法LPP从欧氏空间推广到黎曼流形上,提出LRK-ASOLPP算法,并应用于高分辨率遥感影像目标分类.1)提取图像每个像素点处的几何结构特征,计算图像特征的协方差描述子;2)通过采用Log-Euclidean黎曼核将协方差描述子投影到再生核Hilbert空间;3)基于流形学习理论,建立黎曼流形上半监督正交局部保持投影算法模型,利用交替迭代更新算法对目标函数进行优化求解,同时获得相似性权矩阵和低维投影矩阵;4)利用求得的低维投影矩阵计算测试样本的低维投影,并用K–近邻和SVM 等分类器对其进行分类.与传统的流形学习算法相比,本文提出的LRK-ASOLPP算法在降维的过程中无需进行图像特征向量化表示,有效保留了数据特征的内蕴几何结构和判别信息,并通过选用无参的Log-Euclidean黎曼核克服了传统核方法中的核参数选择问题.实验结果表明,该算法在高分辨率遥感影像目标分类方面具有良好的分类性能,为后续的图像目标分类与识别研究提供了有效的方法.但该算法还有很大的研究空间,例如采用多核学习法来克服核函数与核参数的选择问题,利用稀疏表示构建相似性权矩阵来克服近邻参数的选择问题等,后续将继续进行相关的研究.

表2 UCMerced LandUse dataset上的最佳分类精度(Ac)及对应特征维数(r)Table 2 The classification accuracy(Ac)and the feature dimension(r)on UCMerced LandUse dataset

表3 WHU-RS dataset上的最佳分类精度(Ac)及对应特征维数(r)Table 3 The classification accuracy(Ac)and the feature dimension(r)on WHU-RS dataset

表4 Quick bird dataset上的最佳分类精度(Ac)及对应特征维数(r)Table 4 The classification accuracy(Ac)and the feature dimension(r)on Quick bird dataset