“CASIO”图形计算器与高中回归分析内容的整合

黄文彬

【摘要】利用CASIO图形计算器解决高中回归分析中的六大问题，把繁杂的数据转化成直观的图形，获得回归方程.

【关键词】图形计算器;回归分析

高中回归分析这一部分内容的特点是数据繁杂、运算量大.这与该部分的重点——让学生体会回归分析的思想相互挤压课堂时间.为了突出思想，课堂上不能有太多的繁杂运算，否则时间不足，将冲淡主题.“CASIO”图形计算器让我们从“疑无路”走到了“另一村”.以下结合两个例子谈谈如何利用计算器减少运算，提高时效，突出思想.

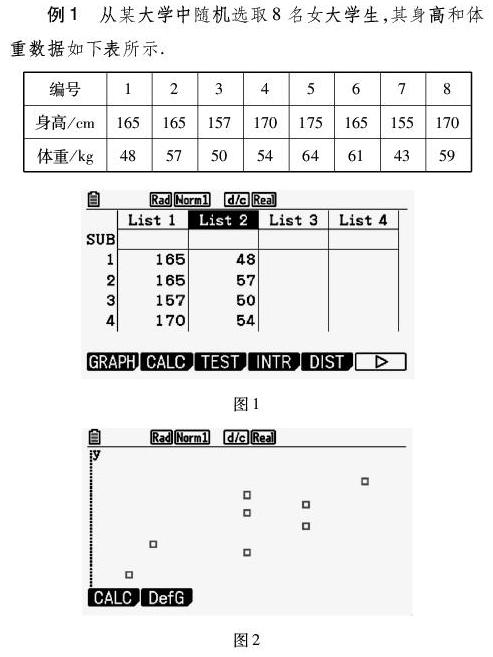
例1 从某大学中随机选取8名女大学生，其身高和体重数据如下表所示.

问题一 制作散点图

步骤如下：第1步，进入统计功能，在List1中输入身高数据，在List2中输入体重数据.结果如图1所示;第2步，按F1进入图形，按F6进入设定，下移光标到第二个图类型，按F1选中散点图.接EXIT退出.按F1进入图1，得到散点图.结果如图2所示.

问题二 计算回归直线方程

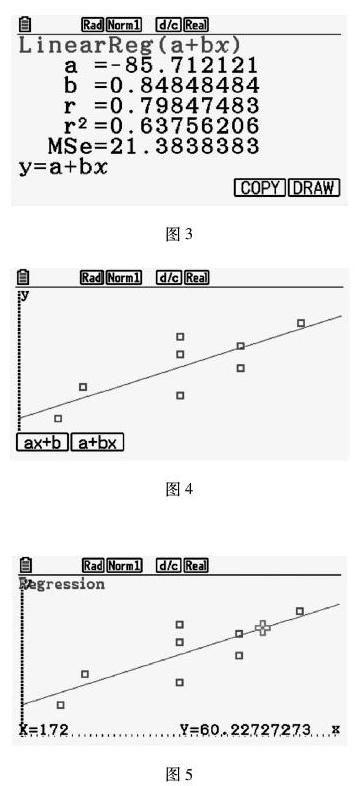
步骤如下：第1步，接问题一，按F1进入回归方程的计算;第2步，按F2选择直线回归方程，再按F2选择第二种类型bx+a.获得回归直线方程的参数值及方程.结果如图3所示.

问题三 计算预报值（预报身高172 cm的女大学生的体重）

步骤如下：第1步，接问题二，按F6绘制回归直线，结果如图4所示;第2步，按SHIFT，按F5，按F1进入求Y值，按F1进入输入X值的界面，输入172，按EXE执行.结果如图5所示.得到身高172 cm的女大学生的体重约为60.22 kg.

问题四 制作残差图

步骤如下：第1步，接问题三，按SHIFT+MENU进入设置，下移光标第二个选项进入残差列表设置，按F2进入列表选择设置，输入3按EXE.设置了List3为残差值的存储空间.按EXIT进入残差表.结果如图6所示;第2步，按F1进入图形，按F6进入设定，下移光标到Y列表，按F1进入列表选择窗口，输入3，按EXE完成设置，按EXIT退出，按F1进入残差图.结果如图7所示.

问题五 回归效果判断

步骤如下：接问题四，按EXIT退出到图形，按F6进入设定，下移光标到Y列表，按F1进入列表选择窗口，输入2，按EXE完成设置，按EXIT退到图形，按F1，按F1，按F2，按F2.结果如图3所示.获得相关系数和可决系数分别为r=0.798，r2=0.638.

问题六 求非线性的回归方程

例2 一只红铃虫的产卵数y和温度x有关.现收集了7组观测数据列于下表中，试建立y关于x的回归方程.

步骤如下：第1步，接问题五，把统计表图中的List1，List2，Listh3中的數据删除.在Lis1输入温度，在List2中输入产卵数;第2步，按F1进入图形，按F1选择图1.结果如图8所示;第3步，按F1进入计算，按F6进入下一个选择菜单，按F3选择指数型回归方程，按F1选择aebx型.获得指数回归的系数值与方程，以及相关系数与可决系数.

从前面六个问题的解决可以看出，利用“CASIO”图形计算器可以很方便地得出结果.借助图形计算器，教师在课堂中可以引入更多更加贴近真实生活的例子，不用担心在课堂中时间不够用，还可以用更多的时间启发学生的思维.学生在课下也能够利用计算器计算身边的回归现象问题，感受数学的魅力与价值.

【参考文献】

[1]人民教育出版社课程教材研究所，中学数学课程教材研究开发中心.普通高中课程标准实验教科书·数学·选修2-3[M].北京：人民教育出版社，2007.