用于含阻尼薄板结构减振的分布式动力吸振器的优化方法研究

朱学治， 刘潇翔， 焦映厚， 陈照波

(1.哈尔滨工业大学 机电工程学院，哈尔滨 150001；2.北京控制工程研究所，北京 100000)

动力吸振器是由Frahm[1]在一个世纪以前发明的。它是一款能够针对特定频率减振的理想装置。由于具有简单、可靠和高效等特点，动力吸振器广泛应用于结构减振降噪工程中[2-4]。吸振器的减振性能对于结构振动特性的误差非常敏感，单个吸振器用于结构减振时，参数设置稍有偏差就会造成减振效果的明显下降。因此，学者们研究了具有自调谐功能的吸振器、多自由度吸振器、复式动力吸振器或者多个频率不同的吸振器组合来克服这些缺点[5-7]。近年来，多个动力吸振器用于连续体的减振的特性得到广泛的研究。研究人员发现，与单个动力吸振器相比，多个动力吸振器用于抑制结构的振动有更好的宽频效果，分布式动力吸振器更容易获得稳健的宽频大范围的减振效果[8-10]。

动力吸振器用于结构减振时，需要经过参数优化调谐才能获得最优的减振效果。目前，用于单自由度系统减振的动力吸振器的优化问题已经有非常完善的方法。Denhartog[11]提出的不动点理论和单个动力吸振器的优化调谐方法是最经典有效的方法。Crandall等[12]提出了用于单自由度减振的单个动力吸振器的H2优化方法。Asami等[13]通过研究提出了用于阻尼线性系统减振的单个动力吸振器的优化调谐方法的解析表达式。

对于单个动力吸振器用于梁板等连续结构减振的优化方法研究也已经比较充足。Jacquot[14]研究了随机激励下动力吸振器对薄板减振的特性，并提出了动力吸振器减振的传递函数用来预测分析动力吸振器的减振效果，还指出了吸振器最优调谐参数的一般规律。Cheung等[15]提出了单个动力吸振器用于薄板结构减振的H∞和H2解析优化公式。Dayou[16]将不动点理论应用到用于连续体整体减振的单个动力吸振器的优化问题中，得到了简洁的动力吸振器调谐公式。

然而，当多个动力吸振器安装在梁板等连续体结构上减振时，多个动力吸振器与主结构组成的动力学系统就复杂的多。对于多个动力吸振器用于连续体结构的减振的优化，研究人员常常采用数值优化算法。尽管各种优化算法的应用能够获得多个动力吸振器的最优减振效果，但是由于算法往往比较复杂，这对于实际工程中的动力吸振器的优化设计不太方便。针对目前的研究现状，并鉴于实际工程中的板类结构往往存在阻尼，本文研究的目的就是通过理论分析提出分布式动力吸振器用于含有阻尼的板类结构减振的参数优化调谐公式。使减振降噪工程中分布式动力吸振器的优化设计有比较简洁且有效的理论依据。

1 理 论

如图1所示，长和宽分别是a和b的矩形薄板上安装有M个动力吸振器，薄板在位置(x0,y0)处受到一个外激励f0(t)。

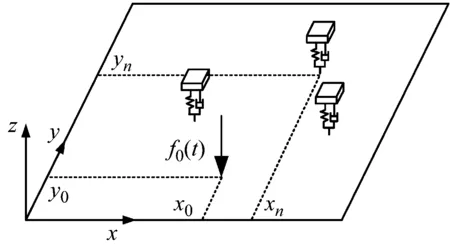
图1 安装了多个动力吸振器的薄板

利用模态叠加法可以得出薄板和动力吸振器组成的动力学系统的运动方程[17]

{P}f0(t)

(1)

其中振动位移向量可以表示为

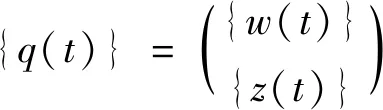
(2)

式中：{w(t)}和{z(t)}分别为薄板各模态和动力吸振器的振动位移向量，它们的表达式分别是

{w(t)}={w1(t),w2(t),w3(t),…,wJ(t)}T

(3)

{z(t)}={z1(t),z2(t),z3(t),…,zM(t)}T

(4)

式中：J为振动系统中一共包含薄板的J阶模态。

{P}为外激励在薄板上的位置分布向量，其表达式为

(5)

这里

(6)

式中：{0}M为M阶零向量。[φ(x,y)]为薄板的模态振型向量，其表达式为

[φ(x,y)]=[φ1(x,y),…,φj(x,y),…,

φJ(x,y)]T

(7)

式中：φj(x,y)为薄板的第j阶模态振型。

式(1)中：质量阵，刚度阵和阻尼阵分别为

(8)

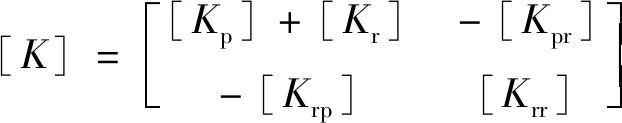
(9)

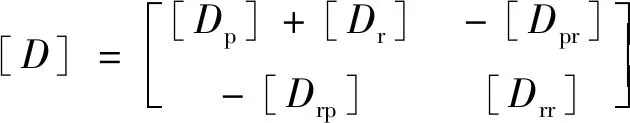
(10)

矩阵中各个子矩阵的表达式分别为：

[Kpr]=[Krp]T=[k1[φ(x1,y1)],k2[φ(x2,y2)],…,kM[φ(xM,yM)]],

[Dpr]=[Drp]T=[c1[φ(x1,y1)],c2[φ(x2,y2)],…,cM[φ(xM,yM)]]

在实际的工程中，振动结构的第一阶模态或者基础模态是最主要的模态，第一阶模态频率往往是动力吸振器应用的目标频率。假设基板的振动以基础模态主导，在简谐运动假设条件下，振动系统的运动方程式(1)可以缩减为

(11)

[D1M]=

[K1M]=

由于动力吸振器的质量阵、刚度阵和阻尼阵在式(11)中是完全对角阵。每个动力吸振器的振动位移只和薄板的振动位移W1相关。根据动力吸振器的振动特征[18]，动力吸振器的振动位移幅值向量可以写成

{Z}=Zref{s1,r,s2,r,…,sn,r,…,sM,r}T

(12)

其中

sn,r=φ1(xn,yn)

(13)

Zref为各个吸振器振动位移幅值的参考值。把式(12)代入到式(11)得到

(14)

式中：

(15)

所有吸振器都具有相同的参数，即每个吸振器的质量、固有频率、阻尼比、刚度分别是mr，ωr，ξr，kr。并记u=mr/M1为质量比，g=ω/β1为激励频率比，f=ωr/β1为固有频率比，δst=f0/K1为系统静变形。

基板振动位移的大小可以表示为

(16)

式中：

Y1={f2-[1+4fξ1ξr+(1+Au)f2]g2+g4}2,

Y2=4g2{(f2-g2)ξ1+f[1-(1+Au)g2]ξr}2。

式(16)与有阻尼单自由度系统附加一个动力吸振器后的振动系统具有相同的特性。经分析，可以得到动力吸振器的最优调谐频率比和最优阻尼比为

(17)

(18)

式中：

C0=52+41Au+8A2u2，

C1=-1 296+2 124Au+6 509A2u2+5 024A3u3+

1 616A4u4+192A5u5,

C2=48 168+112 887Au+105 907A2u2+49 664A3u3+

11 632A4u4+1 088A5u5

当基板无阻尼时，动力吸振器的最优调谐频率比和最优阻尼比退化为

(19)

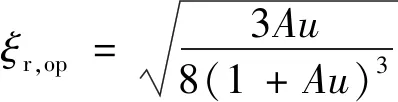
(20)

2 数值计算与讨论

2.1 优化公式的数值计算验证

优化调谐公式是通过式(14)表示的简化的二自由度振动系统推导得到的。优化调谐公式能否适用于原“阻尼薄板-分布式动力吸振器”振动系统，可以通过计算原振动系统的振动响应来分析验证。根据式(1)可以计算得到原振动系统的振动响应

{Q}=(-ω2[M]+jω[D]+[K])-1{P}f0

(21)

其中振动位移表达式为

(22)

薄板各阶模态以及各个动力吸振器的振动位移表达式分别可以写成{w(t)}={W}ejωt和{z(t)}={Z}ejωt。

计算分析中，M个动力吸振器均布在薄板上，分为ra行和rb列。每行与每列吸振器之间以及外边动力吸振器到薄板边缘的距离为a/(ra+1)和b/(rb+1)。

薄板和动力吸振器的参数设置，如表1所示。

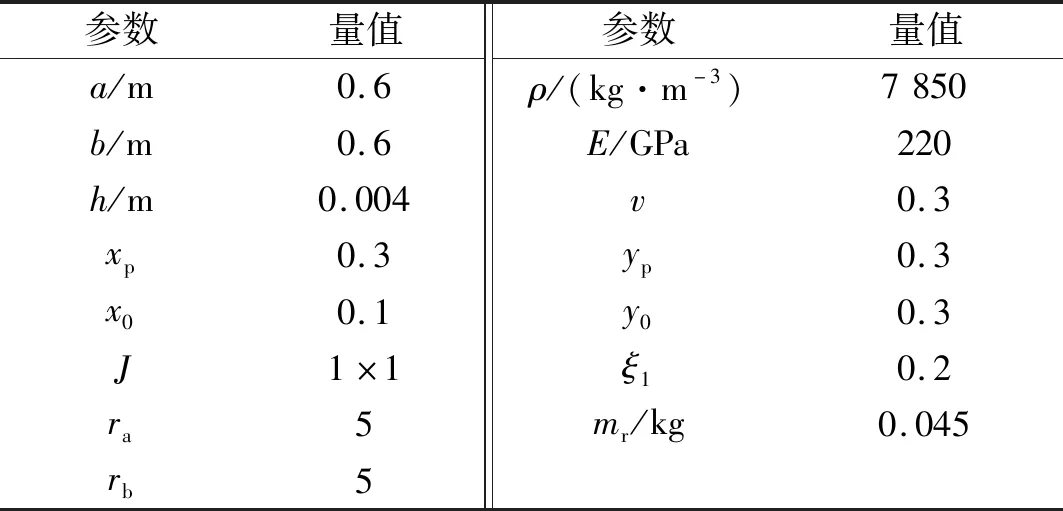
表1 薄板和动力吸振器的参数设置

通过式(21)计算得到由第一阶模态主导的薄板的振动位移，如图2所示。图2中实线表示未安装吸振器时，阻尼薄板的振动响应。其他几条曲线表示安装动力吸振器后薄板的振动响应。安装阻尼薄板上安装分布式动力吸振器后，薄板的振动得到明显的抑制。图中的点划线表示吸振器的参数是根据本文的优化方法来设定的。点线代表吸振器参数经过Denhartog的经典调谐公式设定，虚线表示吸振器的参数是任意设定值。对比几条曲线容易得知，任意设定吸振器的参数具有很大的盲目性，吸振器往往达不到最好的减振效果。经典调谐公式虽然对单自由度系统中的单个动力吸振器有很好的优化结果，但它并不适用于连续体上安装的多个动力吸振器的优化。根据本文的优化方法设定动力吸振器的参数后，薄板振动响应曲线上的两个峰值取得相同的振动量。这证实了本文的优化调谐公式对于优化阻尼薄板结构上的分布式动力吸振器参数的有效性。

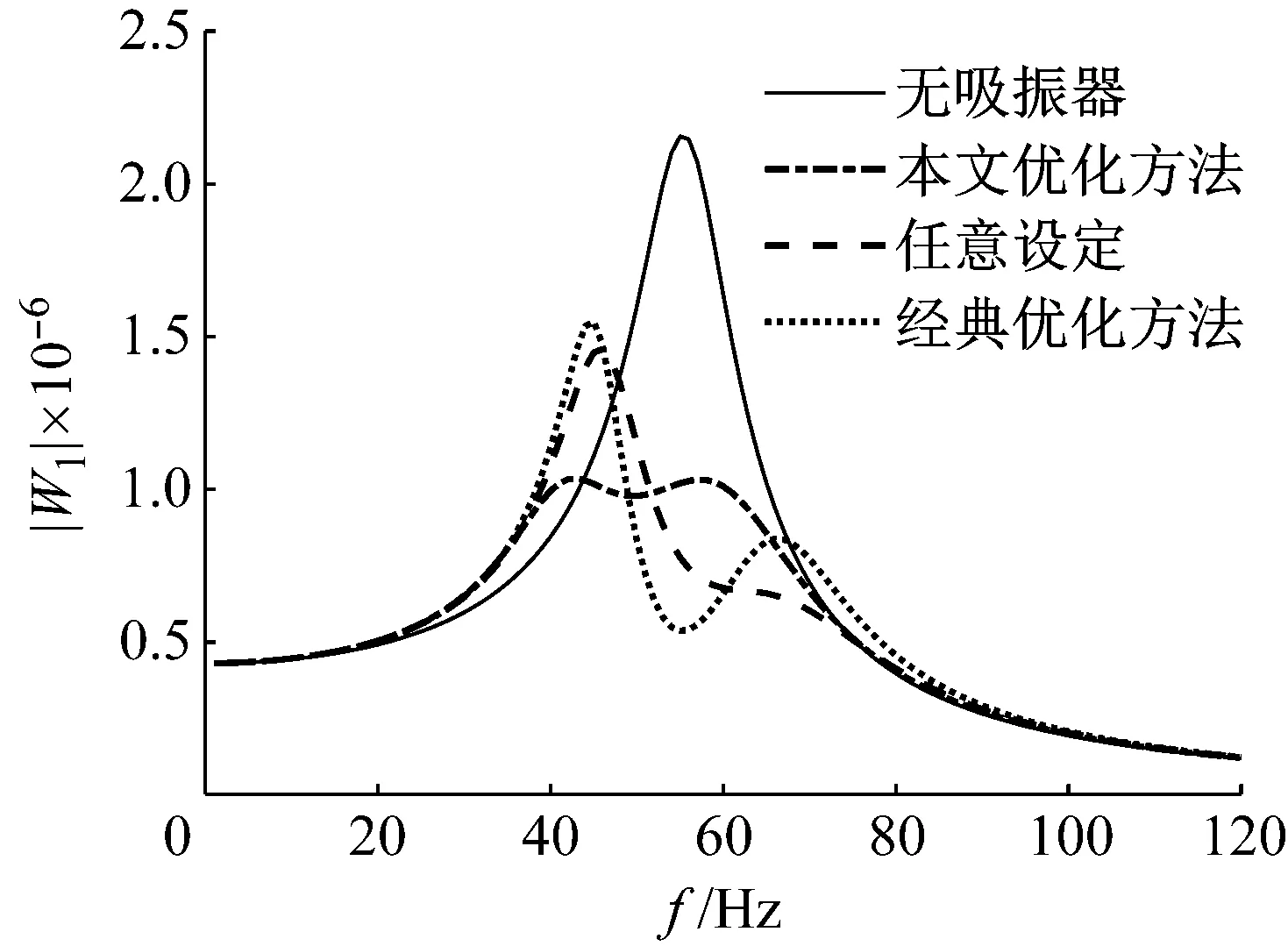
图2 薄板的单模态振动响应

本文中优化公式是以“薄板的振动以第一阶模态主导”为假设条件推导得到。但实际上，薄板的振动还有高阶模态的贡献量。因此，当计及薄板的多阶模态从而使得薄板发生真实的振动情况时，本文提出的优化公式是否还适用，以及相对于经典优化公式是否还有优势需要进行验证。通过式(21)计算得到薄板的多阶模态振动位移后，可以求得薄板的综合振动

w(x,y,t)=[φ(x,y)]T{W}ejωt

(23)

这里需要注意，式(21)所示的薄板振动响应的求救是根据薄板的振动方程式(1)直接求逆得到，求解过程中不含有任何假设及简化，因此求得的结果是 “逻辑绝对正确”的结果。将薄板的阻尼设置为0.15，计及的模态共“7×7”49阶模态，经过优化调谐的吸振器的减振效果，如图3所示。将图3中各个参数设置所取得的减振曲线与图2中相应的曲线进行对比，不难发现，尽管计及了薄板的多阶模态，吸振器对薄板的真实振动抑制效果与对薄板一阶模态振动抑制效果是一致的。也即，本文提出的优化方法能够对吸振器进行优化调谐从而够获得对薄板真实振动的最理想的抑制效果。

图3 包含多阶模态的薄板的振动响应

2.2 优化公式对薄板综合振动抑制的优化效果

吸振器在实际应用中，其最优调谐减振效果有可能受到薄板其他阶模态的阻尼的影响，本部分分析薄板的高阶模态阻尼对最优调谐吸振器的减振效果的影响。将薄板设定为无阻尼(ξj=0)、小阻尼(ξj=0.03)、中阻尼(ξj=0.15)和大阻尼(ξj=0.3)4种阻尼状态，分别计算薄板含有不同数量的模态阶数(J=1×1,2×2,3×3,7×7)时，在每种阻尼状态下的综合振动。选定薄板的中心点(xp,yp)为振动响应拾取点。计算结果如图4～图7所示。

对比各图中的实线代表的无阻尼薄板的低频综合振动： 图4表示薄板的振动以其第一阶模态主导，当算例中计及的薄板的模态阶数增加后(见图5～图7)，薄板的综合振动量没有明显的提高。当薄板中的阻尼值增加后，计算中高阶模态的引入也没能导致薄板综合振动量的明显提升。因此，在包含薄板一阶模态频率的低频范围内，薄板的振动是以其一阶模态主导的。

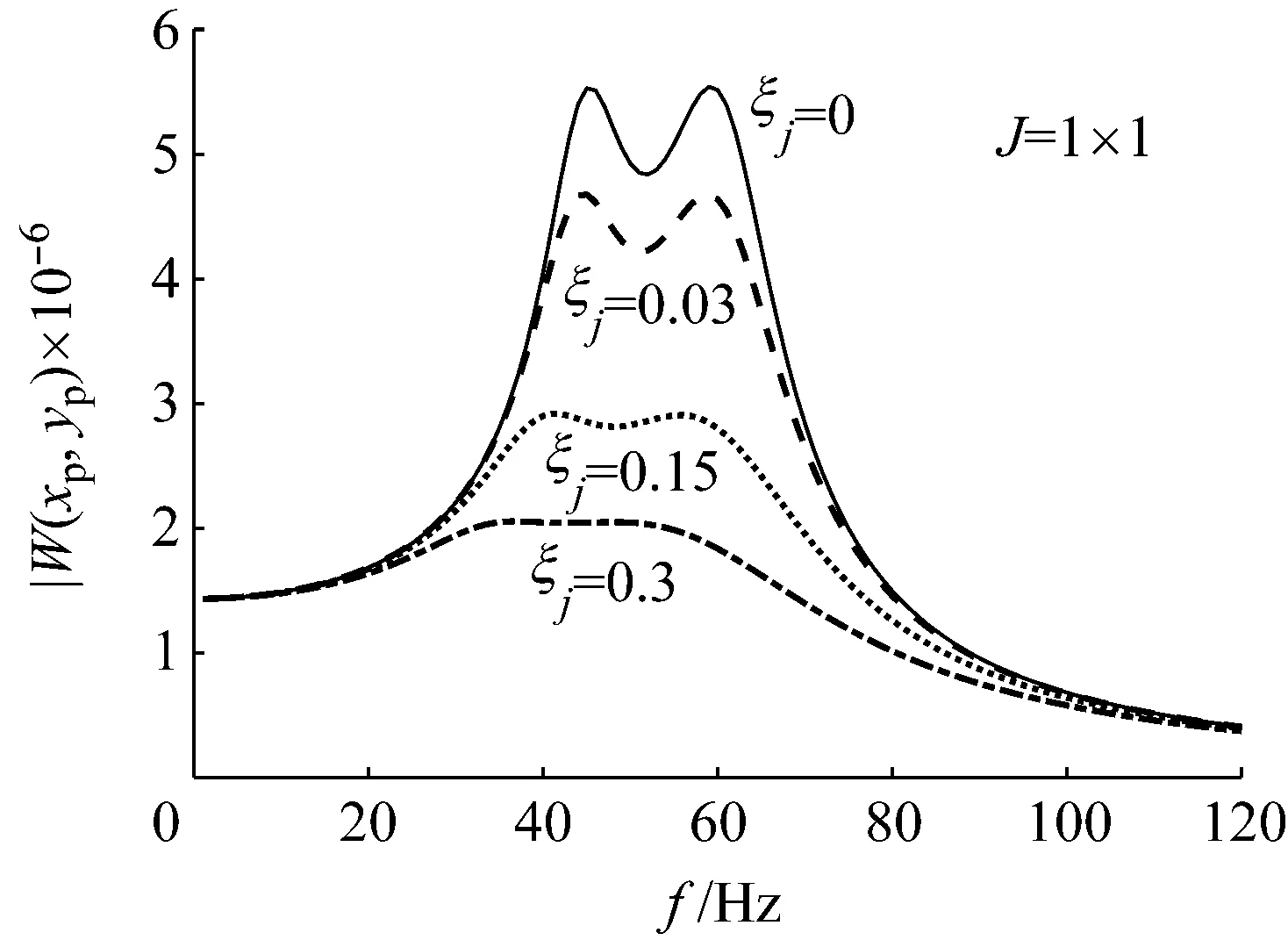
图4 包含1×1阶模态的薄板的振动响应

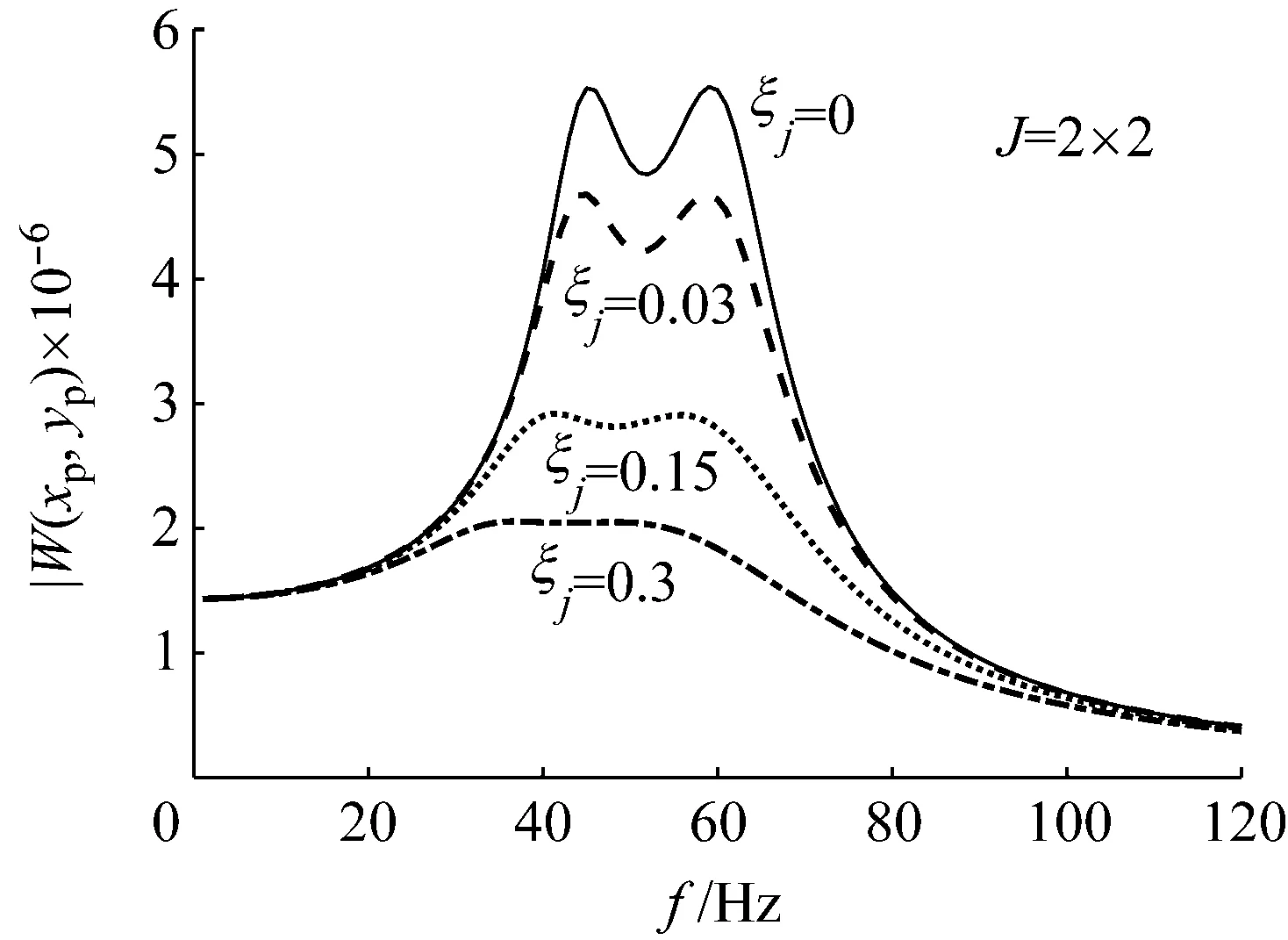
图5 包含2×2阶模态的薄板的振动响应

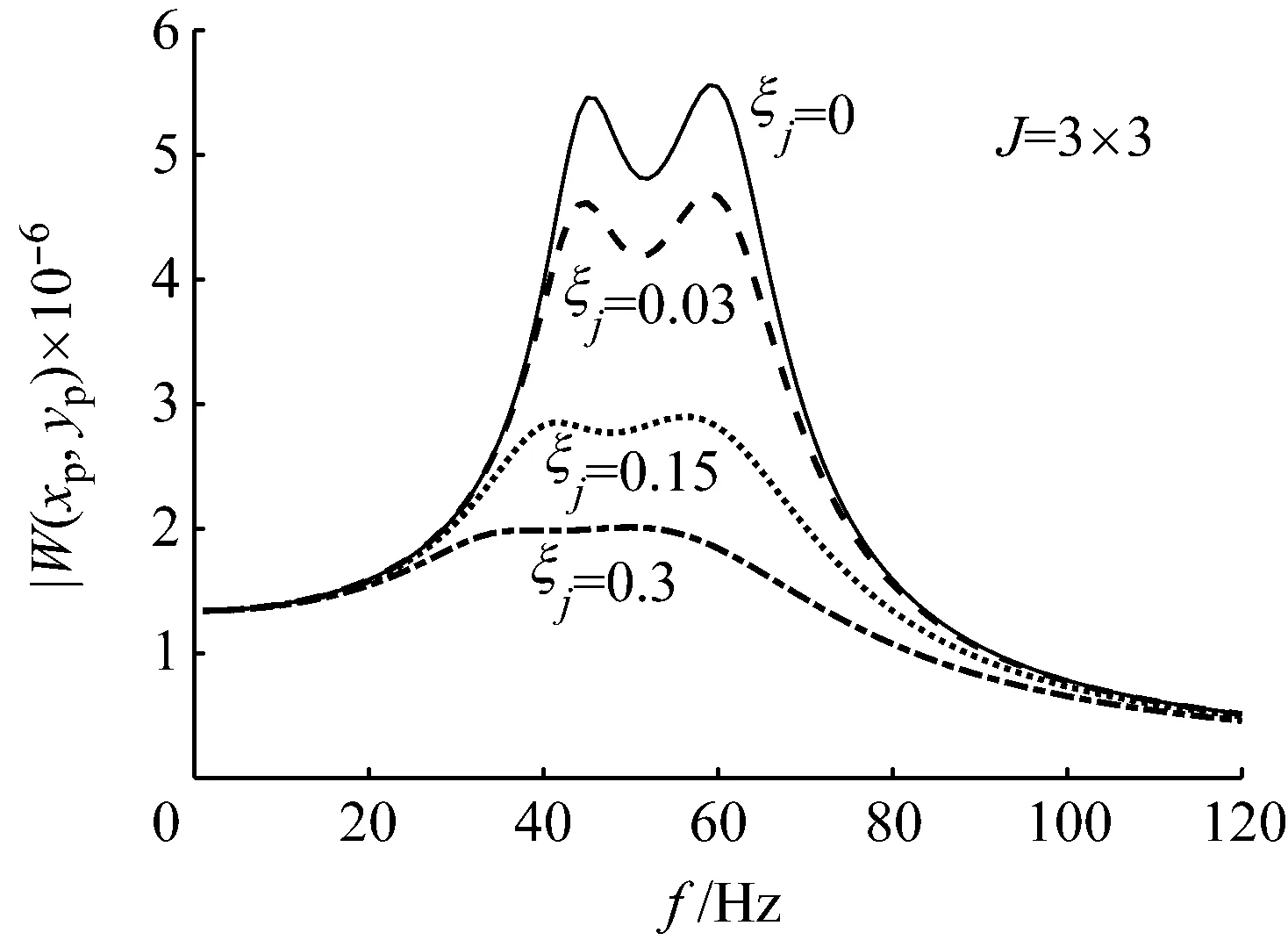
图6 包含3×3阶模态的薄板的振动响应

图7 包含7×7阶模态的薄板的振动响应

在图4和图5中，薄板综合振动响应的算例中计及的模态阶数分别是1×1和2×2。在这两种模态数量的情况下，薄板在各个阻尼状态下的振动响应曲线上的双峰都取得了相同的振动位移，本文中的优化公式取得了理想的优化效果。当更多的模态参与到振动响应计算中后，薄板振动响应曲线上的两个振动位移峰值的量值产生了差值，如图6和图7所示。但是，从图7也可知，尽管参与计算的模态数已经很大，两个振动位移峰值的差值并不显著。而且，随着薄板阻尼值的提高，两个峰值的量值趋于相同。因此，采用分布式动力吸振器来抑制含阻尼薄板结构的特定共振频率处的振动时，利用本文提出的优化公式来调谐吸振器的参数能够获得理想的最优减振效果。

3 结 论

(1) 本文研究了用于抑制薄板结构低频振动的分布式动力吸振器的优化方法。以“薄板的振动以其第一阶模态主导”和“每个动力吸振器都具有相同的参数”为假设条件，并采用含阻尼线性系统中吸振器的最优参数的求解方法，推导得到了分布式动力吸振器的最优调谐频率比和最优阻尼比的解析表达式。

(2) 考虑到薄板结构在工程应用中不可避免的存在阻尼，为了使本文的研究更加贴近于实际，薄板中的阻尼以模态阻尼比的形式引入。

(3) 本文推导得到的解析优化公式的形式与经典的单自由度系统中吸振器的调谐公式的形式相似，但是分布式动力吸振器的最优调谐频率比和最优阻尼比还与吸振器在薄板上的安装位置及薄板的阻尼比相关。

(4) 本文提出的优化调谐公式通过数值计算得到了验证。数值计算分析还表明，尽管优化公式是以“薄板是单一模态振动”为假设条件推导得到，薄板结构振动中的其他模态的贡献量以及其他模态的阻尼对优化效果的影响很微小。

(5) 本文推导得到的优化调谐公式可以很便捷的应用在分布式动力吸振器的设计中，从而获得对含阻尼薄板结构共振频率处综合振动抑制的最优效果。