随机载荷作用下某导弹挂架的疲劳寿命分析

马咪娜，喻 琴

（庆安集团有限公司，陕西 西安710077）

0 引言

飞机在飞行中，除了会受到飞机本身的振源所引起的振动影响外，还会受到由于机翼—外挂气动力所引起的振动影响。一般情况下，这些动态载荷是具有随机型的[1]。为了使悬挂装置的结构能经受得住预期的动态振动应力，确保悬挂装置不会由于使用中的振动而导致性能降低或出现故障，可以通过振动试验确定。由于振动试验需要耗费一定人力、物力及财力，通常先通过振动仿真试验对结构进行分析，最终确定振动试验模型及方案，这样可降低成本。

国内外学者对飞机结构振动疲劳进行了大量的研究。Crandall早在1958年就将随机振动理论应用于结构疲劳研究中[2]；Valanis推导了结构振动疲劳寿命与激励频率之间的关系[3]；周敏亮对飞机结构振动疲劳分析方法进行了研究[4]；罗杨阳采用有限元方法计算了某型导弹吊挂的随机振动疲劳寿命，同时研究了吊挂的结构参数对振动疲劳的影响[2]；周凌波对航空典型结构进行了模态分析试验和宽带随机振动疲劳试验，得到各组试验件的试验寿命值[5]。

本文基于随机振动基础理论和有限元分析理论，利用有限元软件Ansys对随机载荷作用下的某导弹挂架结构了进行振动仿真分析，得到结构在频域上的动应力响应功率谱密度函数[6]，并详细分析导弹挂架的动态响应特征及薄弱环节，计算了导弹挂架的振动疲劳寿命，对导弹挂架的设计具有工程指导意义。

1 振动疲劳寿命分析

随机振动是指无法用确定性函数来描述，但又有一定统计规律的振动，它的特性只能用统计参数描述[7]。概率反映随机事件出现可能性的大小，随机变量是用数量描述随机事件的结果，随机过程即是描述随机变量的发展过程。振动理论的核心概念是随机过程[8]。

随机过程中比较容易计算，已经在工程中得到广泛应用的是平稳随机过程。它的特点是其概率性不随间变化。在平稳随机过程中最为重要的一类，是具有各态历经性的平稳随机过程。如果一个平稳随机过程是由集合平均和时间平均的带的所有各组概率特性都相等，那么就认为这类平稳随机过程具有各态历经性。也就是说，其中任意一条样本曲线基本上包含了该随机过程所具有的所有统计特性。因此，对于这类随机过程，只需测量到一条实测曲线，就可以由它得到各种所需的统计参数[9]。

本文所涉及的随机振动疲劳问题均基于平稳、各态历经样本函数的概率密度函数服从正态分布的高斯随机过程[9]（见图1）的假设，基于模态叠加法，并采用功率谱法进行研究，基于功率谱密度（PSD）的振动疲劳寿命频域分析结构振动疲劳寿命，计算方法简便，且工程适应性强[10]。

图1 高斯过程

1.1 随机过程中的重要参数

PSD函数是描述平稳各态历经过程的最重要参数，随机振动中的连续瞬态响应只能通过概率分布函数进行描述，利用PSD可以获得随机应力信号的均方根值、谱矩、峰值概率分布和峰值频率等信息进而进行累积损伤计算。

随机过程的谱矩是PSD函数的面积对纵坐标的惯性矩，用它可以求出随机过程分析中用到的各种谱参数，谱矩定义如下[10]：

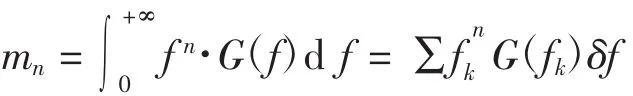
在疲劳分析中利用谱矩表示峰值频率：

1.2 随机振动疲劳校核方法

本文运用基于高斯分布和Miner线性累计损伤定律的三区间法疲劳损伤模型对结构振动疲劳寿命进行校核。此方法的主要优点是结构的动态特性和局部的随机应力可以从计算机辅助工程CAE软件来模拟确定[11]。

对于一个雨流循环来说，其单位时间计数循环数与峰值期望率相等，即v=V[P]。

损伤计算将应力幅值的概率密度函数按概率分布近似划分为三个区间，计算公式为：

其中，n1σ等于或低于1σ水平的实际循环数（0.683vT）（T为振动时间），n2σ等于或低于 2σ 水平的实际循环数（0.271vT），n3σ等于或低于3σ水平的实际循环数（0.043vT）[10]。

N1σ，N2σ，N3σ等于根据 S-N曲线查得的 1σ、2σ 和3σ应力水平分别对应的许可循环的次数。寿命计算为：

2 某导弹挂架有限元分析

2.1 模型建立

某导弹挂架结构示意图如图2所示。

图2 挂架结构示意图

利用Ansys Workbench软件进行有限元计算，对某导弹挂架结构进行简化，将去掉的零件质量以及导发架以集中质量形式连接到骨架、接头及连接螺套上，空载时不加导弹质量点，加载时导弹以质量点形式连接在连接孔处，有限元模型如图3所示。

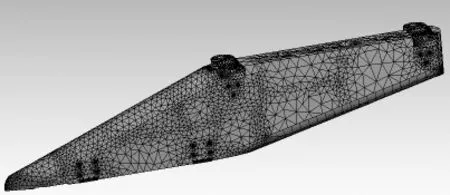
图3 有限元模型

2.2 边界条件

对接头的螺栓孔施加远端点位移约束。

挂架分别在空载和加载（挂装导弹）状态下，对整机产品进行垂直方向上的耐久振动试验。试验振动谱见图4。

a）空载：振动试验按曲线B进行，时间为307 min；

b）加载：振动试验按曲线A进行，时间为307 min。

图4 振动曲线

3 计算结果

3.1 模态分析结果

首先运用Ansys Workbench的对某导弹挂架进行模态分析，其空载及加载时的模态结果如图5所示。

图5 模态结果

3.2 随机振动结果

挂架进行随机振动分析，得到应力分布以及PSD曲线[12]，通过自行对随机振动疲劳计算方法进行Matlab编程，可得到某导弹挂架各状态下的疲劳安全系数。

空载及加载时，对产品施加功能及试验振动谱后，结果显示耳片位置为危险部位。模型在随机激励下的1σ应力分布、耳片的危险部位及如图6所示。

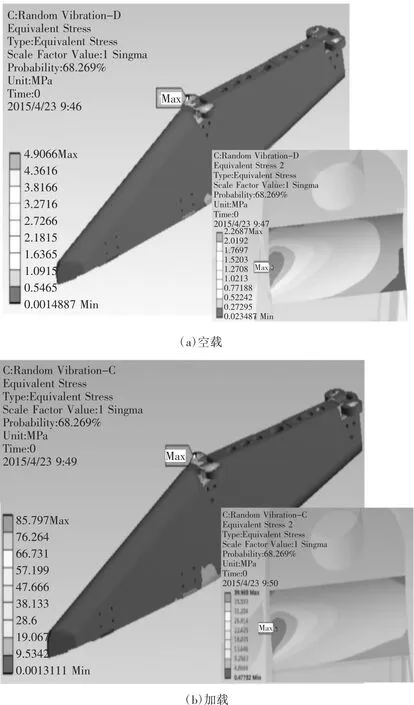
图6 随机激励下的应力分布

提取应力频率响应PSD表，结合材料疲劳性能，即疲劳极限为560 MPa。经计算得到随机振动作用下疲劳寿命系数：空载时为4.03E+06，加载时为47.82。寿命系数均大于1，结果表明：在给定振动激励下，导弹挂架结构满足振动疲劳寿命要求。

4 结束语

（1）本文利用Ansys workbench有限元分析软件，对某导弹挂架结构在随机载荷激励作用时进行了动态仿真分析，准确有效地找到了挂架疲劳强度薄弱的区域为耳片位置，结合随机振动疲劳寿命分析理论对导弹挂架进行力振动疲劳寿命分析，结果表明导弹挂架满足疲劳强度要求。

（2）采用本文的仿真分析方法简单有效反映了结构的应力分布以及强度薄弱位置，指导设计人员在设计初期积极地控制产品的抗振疲劳性能，有效避免在设计阶段反复迭代的情况，从而降低开发成本，缩短研制周期，提高设计方案的成功率。

（3）三区间法估算随机振动疲劳方法具有明显的高效性和高精度特性，能够达到工程设计的要求，计算方法简便且工程适应性强，具有广阔的研究前景和工程应用价值。