应用型人才培养目标下概率论与数理统计课程教学探索
张宇红 刘怡娣
【摘 要】本文结合概率论与数理统计课程的特点,以应用型人才培养为目标,从“教学内容“”教学方法“和”考核方式“三个方面,对概率论与数理统计课程教学进行探索,其宗旨要培养学生的创新能力和解决实际问题的能力。
【关键词】应用型;概率论与数理统计;教学内容;教学方法;考核方式
中图分类号: O21-4;G642 文献标识码: A 文章编号: 2095-2457(2019)12-0120-002
DOI:10.19694/j.cnki.issn2095-2457.2019.12.057
【Abstract】Combining the characteristics of probability and mathematical statistics,this paper aims at the cultivation of applied talents, and explores the teaching of probability and mathematical statistics from the three aspects of"teaching content","teaching method"and"assessment method".It is necessary to develop students'ability to innovate and solve practical problems.
【Key words】Applied talents;Probability and mathematical statistic;Teaching content;Teaching method;Assessment method
概率论与数理统计研究的是随机现象的数量规律性及其应用,在自然科学、社会科学、管理科学、技术科学和工农业生产等各个学科和领域中都具有广泛的应用,是高等院校各类专业大学生最重要的数学必修课之一。一方面,它独特的理论和研究方法使人耳目一新;另一方面,学习该课程需要中学数学和微积分理论作支撑,加之各种新概念、新记号繁多,又使一些初学者颇感困惑。近年来,随着我国教育事业的发展,客观上也给教育工作者提出了新的研究课题。2018年9月,习近平总书记在全国教育大会上强调,要提升教育服务经济社会发展能力,着重培养创新型、复合型、应用型人才。因此在应用型人才培养目标下,我们需要不断总结经验,探索规律,从教学理念和教学方法上适应新形势的要求,激发学生的学习兴趣,培养创新能力和将理论知识应用到实际问题的能力。
1 教学内容需要调整
1.1 概率有重点的讲,统计要多讲
一方面,概率论中“古典概型”和“离散型随机变量的分布律、数字特征”等内容在高中已经学过,学生对于概率论的学习是有一定基础的,因此在学时有限的前提下,避免重复,对于高中已经详细学过的概率论部分,以复习的方式一带而过,对于“连续型随机变量”、“二维随机变量”和“數字特征”等高中略讲或不涉及的章节重点讲授。另一方面,对于在实际生活中应用很广泛的数理统计部分,建议重点讲解,除了参数估计和假设检验外,增加实用性较强的回归分析和方差分析。
1.2 理论推导略讲,应用实例多讲
用通俗的语言和熟知的实例为背景,提炼出抽象难懂的概念,循序渐进地揭示研究方法,在保证知识体系完整的前提下,适当削弱理论深度。在例题和习题的配置上,注意示范性、多样性和趣味性。每一章多介绍应用实例,既可以开阔眼界,活跃思想,加深对本章知识的理解,又可增强应用意识,提高应用能力。
以“全概率公式和贝叶斯公式”这一节的例题为例:设某工厂有三条生产线A,B和C,生产同种产品,其中A完成20%的生产任务,B完成70%的生产任务,C完成剩余10%的生产任务。由于各条生产线机器自身的缺陷以及使用年限等原因,这三条生产线的次品率A为3%,B为1%,C为5%。从三条生产线的产品中随机取出一件产品进行检测,发现是次品,求它分别由生产线A、B、C生产的概率。
通过计算可得:由生产线A生产的概率为0.33,由生产线B生产的概率为0.39,由生产线C生产的概率为0.28.在此结果上,我们可以进一步引申:贝叶斯公式计算的是后验概率,通常用来做决策,比较这三个数值,发现0.39最大,所以该次品最有可能由生产线B生产,其次是生产线A,最后是生产线C。这种情形下,如果考虑对生产线进行调整,首先应该调整B.虽然这种安排不一定每次都是正确的,但总体而言仍是最为合理的排查方式。
1.3 教学内容要结合专业的特点和需求
根据不同专业的学生,结合专业的特点和需求,制定不同的教学大纲,在教学内容上设置符合专业背景的例题。
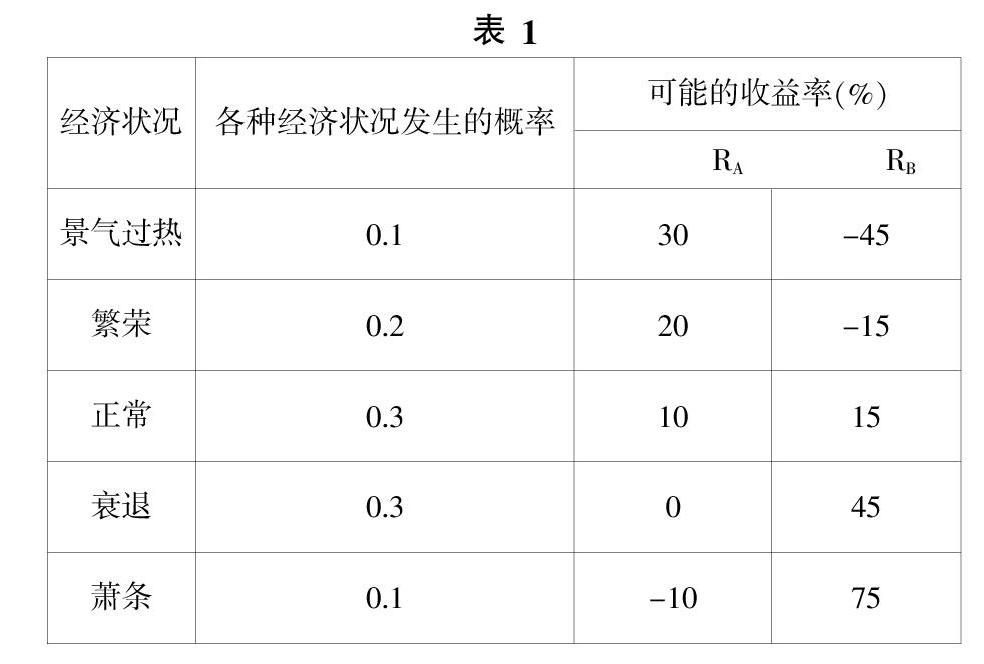
例如数学期望和方差这一节,面对经管类学生,可设这样例题:现有股票A与股票B,在未来不同经济状况下的可能收益率见表1。
要想获得最大收益,应选择哪种股票?若想风险较小,又选择哪种股票?
通过计算期望,得E(RA)=9%,E(RB)=18%。由E(RA)< E(RB),若想获得最大收益,应选择股票B。但投资也要尽量规避风险,可考虑标准差,得 。我们不难发现,股票B的预期收益率虽然是股票A的两倍,但股票B收益率的均方差是股票A收益率均方差的三倍左右,均方差越大风险也大,所以若想投资风险较小,应选择股票A。
1.4 增加实验教学
在教学上,除了理论方面的学习,还需要增加实验实践环节。Excel中有专为统计设计的各类统计函数,可以简化函数的计算,Excel中还有数据分析工具,可将复杂的统计分析过程变得简单。Matlab有较强的绘图能力和随机事件的统计模拟能力,能直观地体现问题及解决过程。通过介绍Excel、Matlab等软件,提高学生借助计算机来应用概率统计方法解决实际问题的能力。
2 教学方法需要多样性
2.1 利用网络课程资源
随着信息技术的发展和广泛应用,通过在线网络课程平台,我们可以接触到很多优秀的网络课程。充分利用这些资源,可以弥补传统课堂教学的不足,激发学生的学习兴趣,提高学生的学习质量。例如,课前通过15分钟关于知识点的学习,学生可对下节课的重点和难点有个大概的了解,这样课堂学习起来更輕松;课后通过15分钟关于习题讲解的学习,学生可对所学的知识得到很好的巩固;另外有些网络课程还包括概率论与数理统计相关的数学家与学科发展史的内容,以及一些概率论与数理统计在实际应用中的例子,这些网络课程作为课堂教学的补充,不但拓宽了学生的知识面,而且提高了学生对概率论与数理统计课程的学习兴趣。
2.2 渗透数学建模思想
概率统计模型是数学建模中应用较多的模型之一。在教学中,可将一些简单的数学建模问题布置成作业,通过小组合作的方式,完成一篇小论文。这样既培养了学生将实际问题抽象为数学问题、建立模型并利用所学知识解决实际问题的能力,也提高了团队合作能力。
3 考核方式需要优化
在应用型人才培养目标下,将应用能力的考核加入到成绩的计算当中是很有必要的。比如平时成绩和期末卷面的比例是3:7,平时成绩除了出勤、作业和期中测验以外,还应该包含实验方面和建模的小论文成绩。
综上所述,在应用型人才培养目标下,概率论与数理统计课程还需要不断的探索与实践,其宗旨要让学生通过大学阶段的学习,对概率论与数理统计这门课程产生兴趣,体会到学习该课程的意义,并提高创新能力和解决实际问题的能力,最终实现应用型人才培养的目标。
【参考文献】
[1]大连理工大学城市学院基础教学部.应用概率统计[M].大连理工大学出版社,2013.
[2]大连理工大学城市学院基础教学部.应用统计学简明教程[M].大连理工大学出版社,2014.
[3]谬铨生.概率与统计[M].华东师范大学出版社,2007.
[4]吕林燕.新课标下高等数学与高中数学衔接问题的探讨[J].山东师范大学学报(自然科学版),2009,24(2):35-36
.作者简介:
张宇红(1979—),女,汉族,锦州人,大连理工大学城市学院,硕士学位研究生学历、教授参与编写教材《应用微积分》和《应用概率统计教材》2部,指导书《应用微积分同步辅导》和《应用概率统计学习指导》2本,在国内外期刊正式发表科研与教学研究论文5篇,其中EI检索3篇(第一作者2篇),核心期刊1篇(第一作者),教育教学论文1篇(第一作者,知网收录)。

