基于调制强度的地铁风机常见故障诊断方法的研究*

宋永兴 伍柯霖 初 宁 吴大转

（浙江大学化工过程机械研究所）

0 引言

地铁风机作为地铁正常、安全运行的重要设备之一，其安全稳定运行具有十分重要的意义。常见的地铁风机故障有地脚螺栓松动、转子不平衡、叶片故障及电机故障等。风机是一种典型的旋转机械，对于其故障诊断，国内外学者开展了广泛的研究，主要包括状态监测、特征提取、故障诊断及状态预测等内容，其中特征提取与故障诊断是其核心内容，也是研究的热点[1]。

对于旋转机械在线监测的信号主要有振动、压力及温度等[2-3]。本文主要针对振动信号的特征提取方法及故障诊断展开研究。针对振动信号特征提取方法，国内外学者开展了大量的研究，主要包括傅里叶变换、短时傅里叶变换、小波变换[4-6]、模态分解[7-9]、包络解调[10-12]及循环平稳解调[13-16]等方法。针对不同的设备采用不同的特征提取方法，能够准确获得旋转机械的特征频率，但是对于设备的故障程度却没有好的指标进行表征。本文中提出了一种调制强度指标，该指标能够准确表征风机的故障程度，结合循环平稳解调算法获得风机的轴频、叶频等特征频率，就可以准确获得风机的故障类型及故障程度。

1 算法研究

1.1 循环平稳分析

风机作为典型的旋转机械，轴频和叶频是反映风机工作状态的重要特征参数，而循环平稳分析是求解旋转机械特征调制频率的有效方法。本文对于循环平稳分析的求解方法，采用法国Antoni学者提出的方法进行求解。

对于风机的振动信号x(t)，其时变的自相关函数可以表示为：

式中，E{}表示求均值运算符号，τ为延迟时间。

其中Rx(t,τ)的傅里叶变换可以表示为：

对于Rαx(τ)的傅里叶变换为谱相关密度函数：

式中，α 表示循环频率，f表示谱频率。

1.2 调制强度

风机在运转的过程中存在明显的调制现象，当故障发生时，风机的调制作用会得到加强，因此通过求解调制分量的强度，能够反映风机的工作状态以及故障程度。对于调制强度的求解，本文主要依托包络Hilbert解调进行求解。

信号x(t)的Hilbert变换的定义为：

式中，H[]为希尔伯特算子。

信号x(t)的包络信号为：

对包络信号进行傅里叶变换：

对于信号的调制强度E定义为：

式中sum()为求和符号。

2 故障实验

针对所提出的基于调制强度的地铁风机的故障诊断方法，分别对实验室风机和地铁射流风机开展故障实验研究，主要对地脚螺栓松动、叶片不均等两种故障展开实验研究。实验中的采集系统采用NI 采集仪（USB-4432.NI Inc），传感器采用振动传感器，采样率设置为5.12kHz。

2.1 实验室风机实验

具体实验装置如图1所示。

地脚螺栓的位置编号如图2所示，风机叶片的位置编号如图3所示，风机故障实验种类如表1所示。

图1 风机实验装置Fig.1 Fan experiment device

图2 地脚螺栓编号Fig.2 Bolt number

式中，α=m/T ，m为整数，T为周期。

图3 叶片编号Fig.3 Blade number

表1 风机故障实验种类Tab.1 Type of fan fault experiment

2.2 地铁射流风机实验

根据调制强度算法，同样开展了地铁射流风机实验。射流风机叶片数量为8 片，实验装置如图4 所示，主要为螺栓松动实验，同样利用振动传感器采集在不同螺栓松动情况下的变化。

图4 射流风机故障实验装置Fig.4 Fault experimental device of jet fan

3 结果分析

3.1 实验室风机

3.1.1 特征频率提取1）螺栓松动

对于实验室风机的螺栓松动的振动信号，采用循环平稳解调算法，能够准确获得风机的轴频及叶频信息，如图5 所示，二者的相对关系同样能够准确地反映出当前叶片数量为6，转速为29.87Hz，叶片并没有发生故障。

图5 循环平稳解调谱Fig.5 Cyclostationary demodulation spectrum

2）叶片不均等

对于实验室风机的叶片不均等故障工况下的振动信号，采用循环平稳解调算法，准确获得了风机的轴频及叶频，如图6 所示，可以发现当前风机的转速为28.86Hz，叶片数量为2，能够准确地反映出当前叶片数量不均等的故障工况。

图6 循环平稳解调谱Fig.6 Cyclostationary demodulation spectrum

3.1.2 调制强度分析

利用循环平稳算法能够准确获得风机的轴频及叶频信息，但是这些信息并不能准确反映出当前风机的故障程度，因此利用本文所提出的调制强度分析进行进一步的分析研究。

1）螺栓松动

针对风机螺栓松动的故障，针对螺栓松动数量，利用调制强度进行分析，得到在不同螺栓松动下的调制强度变化如图7所示，A表示调制强度的幅值，N表示螺栓松动的数量，随着螺栓松动数量的增加，风机的不平衡程度增加，此时所得到的调制强度也逐渐增加，调制强度与螺栓松动的数量呈现正相关，表明利用调制强度变换能够很好地表征螺栓松动的数量。

图7 调制强度Fig.7 Modulation intensity

2）叶片不均等

针对风机叶片不均等的故障工况，实验中分别对两叶片和三叶片进行了调制强度分析如图8所示，图中的横坐标表示风机的排布方式，对于两叶片工况，以叶片的排布方式的不平衡度来讲，存在12布置>13布置>14布置；对于三叶片排布方式的不平衡度来讲存在123布置>124布置>135布置；因此，利用调制强度分析能够很好地说明叶片的布置关系，与不平衡分布状况能够很好地对应起来。

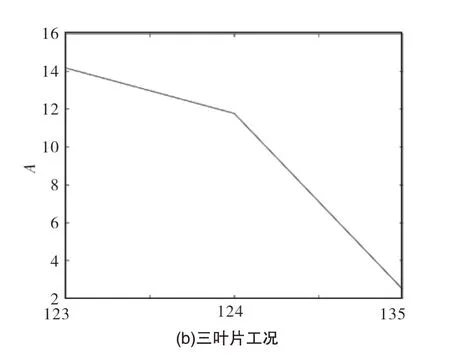
图8 调制强度Fig.8 Modulation intensity

3.2 射流风机

3.2.1 特征频率提取

对于射流风机螺栓松动工况的振动信号，利用循环平稳解调算法，能够很好地解调出风机的轴频和叶频如图9 所示，分别为49.62Hz 和396.9Hz。该方法能够准确的表明风机的工作状况，以及射流的叶片数目为8。

图9 循环平稳解调谱Fig.9 Cyclostationary demodulation spectrum

图10 调制强度Fig.10 Modulation intensity

3.2.2 调制强度分析

针对射流风机的螺栓松动实验，考虑到风机固定方式和实验安全性，只是对螺栓松动数量为0,1,2 三种工况进行了实验研究，利用调制强度分析的结果如图10所示，横坐标表示螺栓松动的数量，能够准确的表明调制强度与螺栓松动数量对应正相关。

4 结论

1）本文针对地铁风机的工作特点，结合振动信号的循环平稳特性，利用循环平稳解调算法对风机的振动信号进行了解调分析，准确的解调出风机的轴频、叶频及谐频等关键信息，有助于风机故障工况的诊断分析。

2）针对地铁风机故障识别困难，以及难以对故障程度进行识别的问题，本文提出了调制强度的解决方法，能够准确的对实验室风机以及现场地铁风机的螺栓松动、叶片不均等的故障工况的程度进行准确的表征，对于风机的故障诊断具有重要的意义。