混合网络中基于约束的信宿计算方法
张 洁
(福建农业职业技术学院,福建福州 350007)
传感网作为集计算机技术与通信技术于一体的混合型网络[1],在检测服务质量(QoS)方面发挥了不可比拟的优势,深受业界的欢迎,同时也在学术界引起了众多关于在混合型网络中实施异常服务计算的思考。常见的计算策略基于非测距计算机制。该机制借助通信节点彼此的关联度[2]来传递节点间的数据包,然后运用分布式计算方法近似地计算出异常信宿所在的坐标信息。但是该方案对节点类型的规模以及混合网络的拓扑具有较高的依赖性。比如,计算待测目标坐标时要求目标必须处于已知节点的广播半径内。这样的研究应用实际上是在对已知节点的规模提出要求。然而实际应用中的混合网络出于成本和布局因素考虑,往往存在已知节点较为稀疏的现象。这种现状显然无法为传统算法的实施提供特定环境。基于上述传统算法的适用性,本文提出一种基于约束的信宿计算方法。
1 传统算法的局限性
传统研究在计算QoS异常的信宿时,多数依赖于大规模已知节点所布局的几何网络区域。运用数学方法为所围建的几何区域进行建模[3],然后展开几何中心的计算。首先,由足够数量的已知节点包围住一个QoS异常的目标信宿节点,建立一个封闭式网络。然后由这些已知节点广播自身信息域给目标信宿,接着计算出封闭式几何网络的中心坐标,作为目标信宿的测量值。
但在目标信宿通信半径范围内分布有大量已知节点的情形下,可知该目标信宿完全有可能位于这些已知节点广播通信的重合区域。传统的算法在对这样情形下的目标信宿展开计算时,往往是以附近已知节点所构建的封闭式几何网络为框架计算几何网络的中心坐标。而事实上并非全部的几何中心坐标都会刚好处在这个重合的区域。

2 基于约束的计算思想
为了改进传统算法在计算精度上的不足,基于约束的计算方法实施于应用型融合网络中必须要将目标信宿通信半径范围之外的已知节点相关数据纳入算法计算的范围。令目标信宿的实际坐标为G(XGS,YGS)、测算坐标为G(XGE,YGE),目标信宿通信范围R里面的已知节点i实际坐标为(Xi,Yi),目标信宿通信范围里面的已知节点O实际坐标为(XO,YO)。则目标信宿满足下列条件:
(2.1)
同时可根据式(2.2)求得测算坐标:
(2.2)
将目标信宿通信范围之外的已知节点到某个节点的间距超过R时的数量规模,与那些目标信宿通信范围以内的已知节点到某个节点的间距小于R时的数量规模,进行相加后再除以全局已知节点的数量规模,如果达到了预置门限值,则基于约束的计算方法认为该方位的附近有一个值得考虑的目标信宿测量值。
在开展约束计算时,首先要选取出距离目标信宿最近的已知节点,再分布式计算出该已知节点周围存在的多个值得考虑的目标信宿测量值,然后确定一个最优测量值[4]。每一次对不同的待测面积展开计算时均设置不同的门限条件值。按照待测网络面积从小到大依次设置门限为0.9、0.8和0.7。首次计算时,与目标信宿间距最短的已知节点作为几何中心,构建出一个正方形待测区域,区域边缘的周长均为半径的两倍。然后将该正方形四等分,估算每个正方形的几何中心值附近是否存在一个值得考虑的目标信宿测量值。如果存在,对该小正方形进行二次计算。计算前仍然进行四等分,然后估算每个小小正方形的几何中心是否存在一个值得考虑的目标信宿测量值。如果存在,则继续进行类似的计算[5]。最终将所分析出来的值得考虑的测量值的数量S,通过函数(2.3)计算出所有测量方位值形成的封闭式网络的几何中心,作为目标信宿最优方位测量值G(XGE,YGE)。
(2.3)
3 基于约束的计算实施
结合基于约束的计算思想,按照如下步骤分布式实施目标信宿计算:首先,在待测混合网络区域内由已知节点向全局发起广播[6],所广播的信息域包含已知节点方位数据,以及已知节点与目标信宿之间的间距数据。其次,遍历出与目标信宿间距最短的那个已知节点,并以该已知节点方位为中心,规划出两倍半径的边缘作为正方形其中的一条边长,构建出八位半径周长的正方形区域。然后,将该正方形四条区域边缘的中点连线,刮分出四个小正方形。再估算出每个小正方形几何中心处附近的那个相对可信的目标信宿测量值。以此类推,连续展开三次计算,得到多个相对可信的目标信宿测量值。最后,对这多个相对可信的目标信宿测量值做加权处理[7],进而求出目标信宿最优方位解。
4 实验分析
4.1 实验模型
在实施约束计算之前,先构建如下测试模型[8]:(1)创建一个如图1所示的100 m×100 m的监测区域作为模拟混合网络的环境,并在该模拟环境中随机部署30个方位信息明确的已知节点和70个普通节点;(2)通过数次变化总节点规模、已知节点规模和通信范围来考察约束计算对目标计算误差的影响;(3)为了防止部署节点的偶然性对实验结果造成影响,每一次实验后均重新部署已知节点和普通节点的密度;(4)节点广播半径范围初始化为20 m;(5)为客观地反映约束算法的性能,实验在300次仿真后才开始收集数据。并根据数据绘制出几何曲线图与传统非测距算法进行比较。
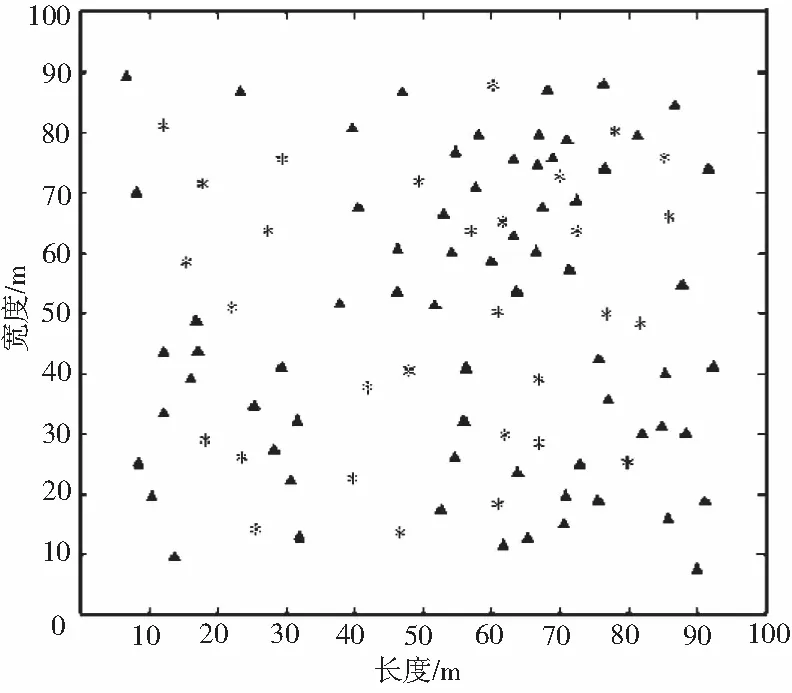
图1 混合网络部署示意图
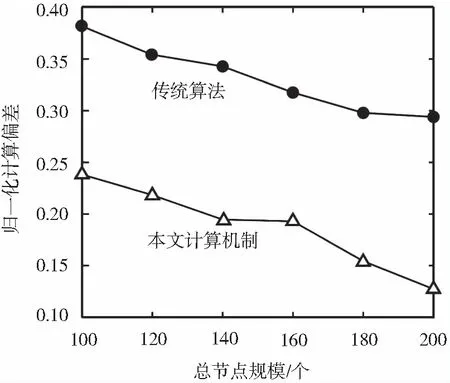
图2 总节点规模对目标计算的影响度
4.2 实验分析
由于混合网络中节点可为目标计算提供有参考价值的信息域[9],故全局中总节点规模数量的增加势必使每个正方形检测区域内节点的密度也同比增加,这在一定程度上为计算目标信宿方位提供了足够数量和足够准确的参考数据。正如图2所描述的总结点规模对目标计算的影响度,两种算法曲线所对应的归一化计算偏差均与总节点规模成反比。但相对于传统算法而言,约束计算方法由于对节点类型的依赖性相对较轻,因此在本项实验中表现出了相对优势。
根据目标计算思想可知,计算精度和已知节点规模呈正比。因此,任何情形下目标计算误差都将伴随着已知节点规模的增加而线性递减。这样的计算特征在图3所示的曲线走势图中得到了验证。图3描述了已知节点规模对计算目标的影响度。由于传统算法对已知节点规模具有较高的偏好度,因此已知节点规模较小时传统算法在计算精度上的劣势表现较为明显,即归一化计算偏差值较高。随着已知节点规模逐渐增加,两种算法的精度均得到了明显提升。但约束计算机制下的归一化计算偏差相对于传统算法仍占据绝对优势。
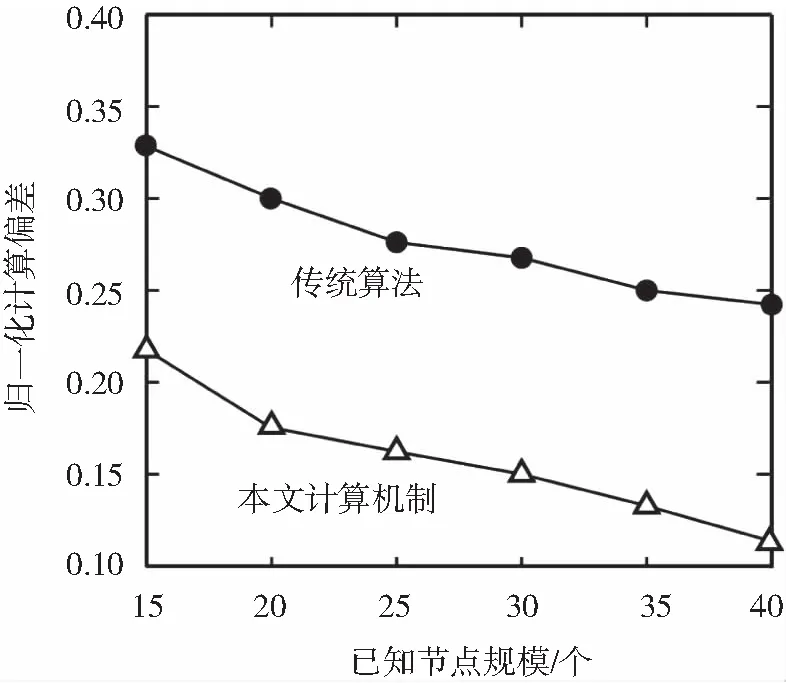
图3 已知节点规模对目标计算的影响度
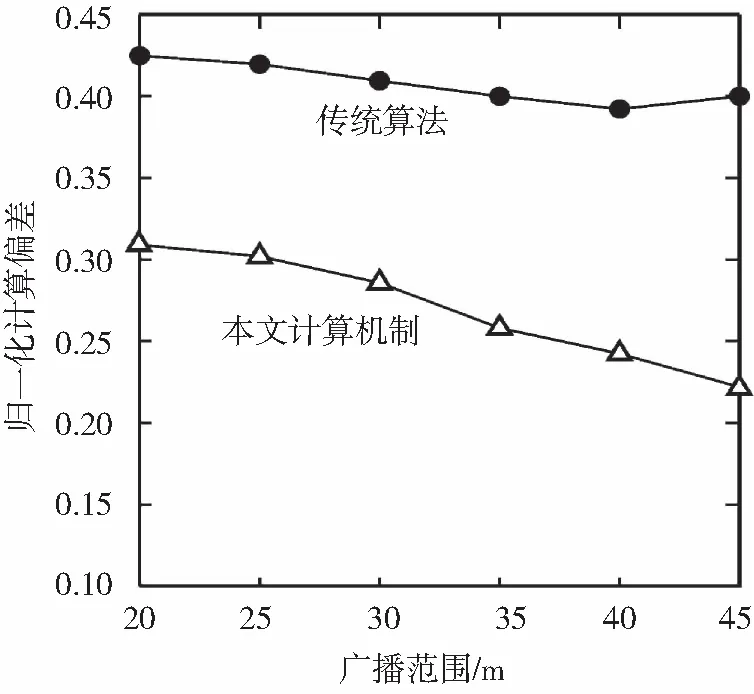
图4 节点广播范围对目标计算的影响度
图4描述了节点广播范围和目标计算精度之间的关系。随着广播半径范围从20 m扩大至30 m,可用已知节点数量相应的增加,目标信宿获得的信息域可靠性[10]也相应增高。因此两种算法曲线对应的归一化计算偏差呈现下降趋势。随着广播范围进一步加大,由于约束算法的计算函数能够利用广播半径扩大后新增的已知节点,使得约束算法在本项考察中体现出优势。
5 结语
本文通过对传统计算机制运用在融合网络中计算异常目标的可行性进行分析,提出了一种适应性较好的异常信宿计算方法。该方法通过充分利用全局范围内的已知节点来为异常信宿的计算过程提供可靠信息域,进而实施对传统算法的改善。经过测试表明,该算法应用在融合网络实施计算具备可行性。

