上向水平分层充填法矿房跨度的确定及采场稳定性分析

罗 瑞，马锟辉

(1.福州大学 紫金矿业学院，福州 350116；2.福州大学 爆炸技术研究所，福州 350116；3.紫金矿业集团股份有限公司，福建 上杭 364200)

采场结构参数是影响地下矿区稳定性的关键因素。对于上向水平分层充填采矿法，矿房跨度是该种采矿方法最重要的采场结构参数之一，若矿房跨度参数设计过小，那么矿石损失率贫化率将升高，矿石回收率将降低；若矿房跨度参数设计过大，那么矿房稳定性将难以保证，在回采过程中，容易发生岩爆、顶板岩石垮落等大规模地压活动的情况。所以合理的矿房跨度是实现矿山经济高效且安全开采的重要参数。对于采场结构参数的确定及优化研究手段有多种。厚跨比法[1]、KB鲁别涅依他公式法[2]等计算方法在矿山现场实际的设计中得到了广泛的应用。刘培正[3]等利用数值模拟软件对采场结构参数及采场稳定性进行了分析。胡高建[4]等运用Mathews法对采场参数进行了优化并在理论层面对采场稳定性进行了判定。研究学者在确定矿房跨度时仅采用了Mathews法或有限元数值模拟，然而单一的采用Mathew法或数值模拟方法都存在一定的缺陷。

本研究以福建某矿山为研究对象，结合Mathew稳定图法与数值模拟方法进行合理的采场结构参数的确定；根据Mathew法首先确定矿房保持稳定的最大跨度，然后通过对设计采场结构参数进行数值模拟，分析设计采场的稳定性。

1 Mathews稳定图法及优化

Mathews稳定图法是20世纪80年代由Mathews等人基于大量工程数据所提出的，早期的Mathews稳定图法使用条件较为苛刻，要求矿体为深部岩体、急倾斜、岩体质量中等稳固以上、岩体硬度高等条件，使用时具有一定的局限性。而后经Trueman[5]多位研究学者收集分析更多的采矿现场数据，对Mathews稳定图法的合理性进行了验证，并在该研究基础上对Mathews稳定图进行了修正，使得Mathews稳定图法在浅部岩体、缓倾斜等多种采矿工况中均能使用，大大减小了该方法的局限性。Mathews稳定图法的基本原理是通过计算得到岩体稳定性指数N与采场形状系数S，将N值与S值在Mathews稳定图中进行投影即可确定采场稳定性，或基于Mathews稳定图由N求得S，进而反算出采场的合理矿房跨度，见图1。

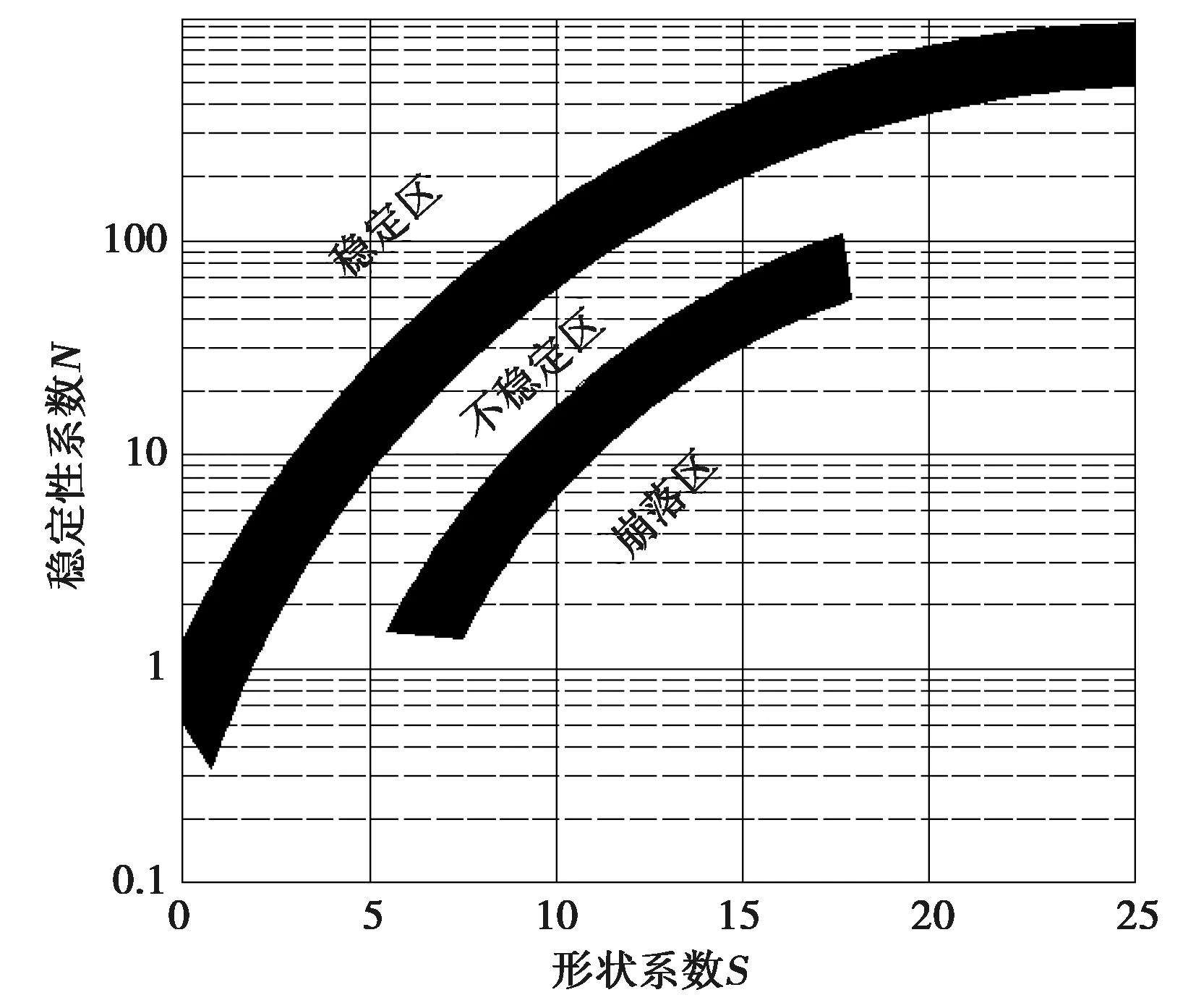
图1 Mathews稳定图Fig.1 Mathews stability graph

2 矿房跨度参数的确定

稳定性系数N的计算公式为：

N=QΔABC

(1)

稳定性系数N表征了岩体保持稳定的强弱，QΔ为岩体质量指数Q考虑节理和水作用后的修正值，A表征岩石应力系数，B表征岩体缺陷方位修正系数，C表征重力调整系数。

1)岩体质量修正指数QΔ。可通过Q值与RMR之间的转化公式[6]。获得：

QΔ=e(RMR-44)/9·Jw/SRF

(2)

式中：Jw表征节理水衰减系数，SRF表征应力折减系数。

2)岩石应力系数A。由岩石抗压强度与诱导应力之比获得：

(3)

3)岩体缺陷方位修正系数B。由图2可得：

图2 岩体缺陷方位修正系数B的确定Fig.2 The correction coefficient B of rock mass defect orientation

4)重力调整系数C。C值可通过采场暴露面的倾角α确定：

C=8-6cosα

(4)

式中，α值即为采场暴露面的倾角。

采场形状系数S由式(5)计算可得：

(5)

式中：L为矿房长度，K为矿房跨度。

Mawdesley[7]于2004年基于矿山现场的稳定、不稳定、崩落所占百分数为式(6)、(7)的概率，以稳定性系数N，采场形状系数S，岩石应力系数A，岩体缺陷方位修正系数，重力调整系数C为因子进行回归分析得公式(8)。

Z=α+β1X1+β2X2+···+βnXn

(6)

(7)

Z=2.960 3-1.442 7lnS+0.792 8lnR

(8)

式中：f(z)为对数概率，Z为对数几率，α为常数，β为回归系数。

本文根据图1及查阅文献[8]对曲线进行拟合，求出稳定性系数N，采场形状系数S的稳定—破坏函数表达式，见式(9)：

lnN=1.889 0lnS-1.209 7

(9)

3 工程应用与分析

矿体主要分布在57～73线之间，矿体多呈走向短，倾向延伸长。标高80～130 m，埋藏深度180～440 m，矿体呈透镜状产出。矿体总体走向北西，倾向北东，倾角60°。矿体与围岩主要由花岗岩所组成，以块状结构为主，岩体的稳定性主要取决于构造破碎带的发育程度和风化程度，岩体较破碎，岩体的稳定性较差。采矿工程主要在花岗岩体中施工，其稳定性主要受断裂和蚀变带的控制，岩石总体完整性较差，岩芯一般呈短柱状，在构造破碎带呈碎块状。岩芯采取率为60%；岩石RQD值为70%，局部地段为10%～20%。

参考矿区花岗岩RMR=50，由公式(2)可得：QΔ=1.704 3。矿岩具体物理力学参数见表1。在工程实际应用中，若岩体为上盘时，应力系数A取值为1。

表1 矿区岩石的物理力学参数

根据矿山地质人员现场地质调查情况并结合图2，岩体缺陷方位修正系数B取0.8。由于采场顶板为水平状态，所以由式(4)可得重力调整系数C取值为2。根据以上数据，由公式(1)可得稳定性系数N为2.726 8，由式(9)计算得矿房形状系数S=3.227，矿体水平厚度即矿房采场长度为10～30 m，矿房垂直矿体走向布置，则由稳定—破坏函数表达式(9)可得采场保持稳定的最大跨度值，采场结构参数如表2所示，顶板暴露面积和顶板跨度变化趋势如图3所示。

表2 采场结构参数表

图3 矿房参数关系图Fig.3 Diagram of the parameters of stope structure

由表2、图3可以确定，矿房垂直矿体走向布置，矿房长度取最小10 m时，矿房最大安全跨度为18 m。

为合理控制回采率和贫化率，取矿房长度为20 m，此时矿房最大安全跨度9.5 m。矿区分层高度取5 m；花岗岩稳定性较好，根据上向水平分层充填采矿法设计，矿房顶柱取4 m，底柱取5 m。采场布置见图4。

4 采场稳定性数值模拟验证

利用SIGMA/W有限元分析程序，对上向水平分层充填采矿法的矿房进行数值模拟，分析矿房的应力应变及位移。分别正面和侧面建立数字模型，模型底部为固定边界条件，四周为对称边界条件，垂直方向为自重应力。

由图5能够看出，采场顶板虽有小范围的应力集中，但整体应力分布均匀，顶板以上区域无剪切和拉压破坏，顶板稳定性良好。上盘围岩所受应力最大值为1.8 MPa，小于花岗岩2.8 MPa抗拉强度，采场围岩稳定，与Mathews稳定图分析结果一致。

由图6可以看出，垂直于矿体走向的采场顶板无明显应力集中，顶板稳定性良好。顶板及以上区域应力分布均匀，未出现剪切和拉伸破坏。最大应力1.4 MPa，小于花岗岩2.8 MPa抗拉强度，采场围岩稳定，与Mathews稳定图分析结果一致。

图4 上向水平分层充填采矿法Fig.4 Upward horizontal layered filling mining method1—顶柱；2—充填天井；3—矿石堆；4—人行溜水井；5—放矿溜井；6—主副钢筋；7—人行溜水井通道；8—上盘运输巷道；9—穿脉巷道；10—充填体；11—下盘运输巷道

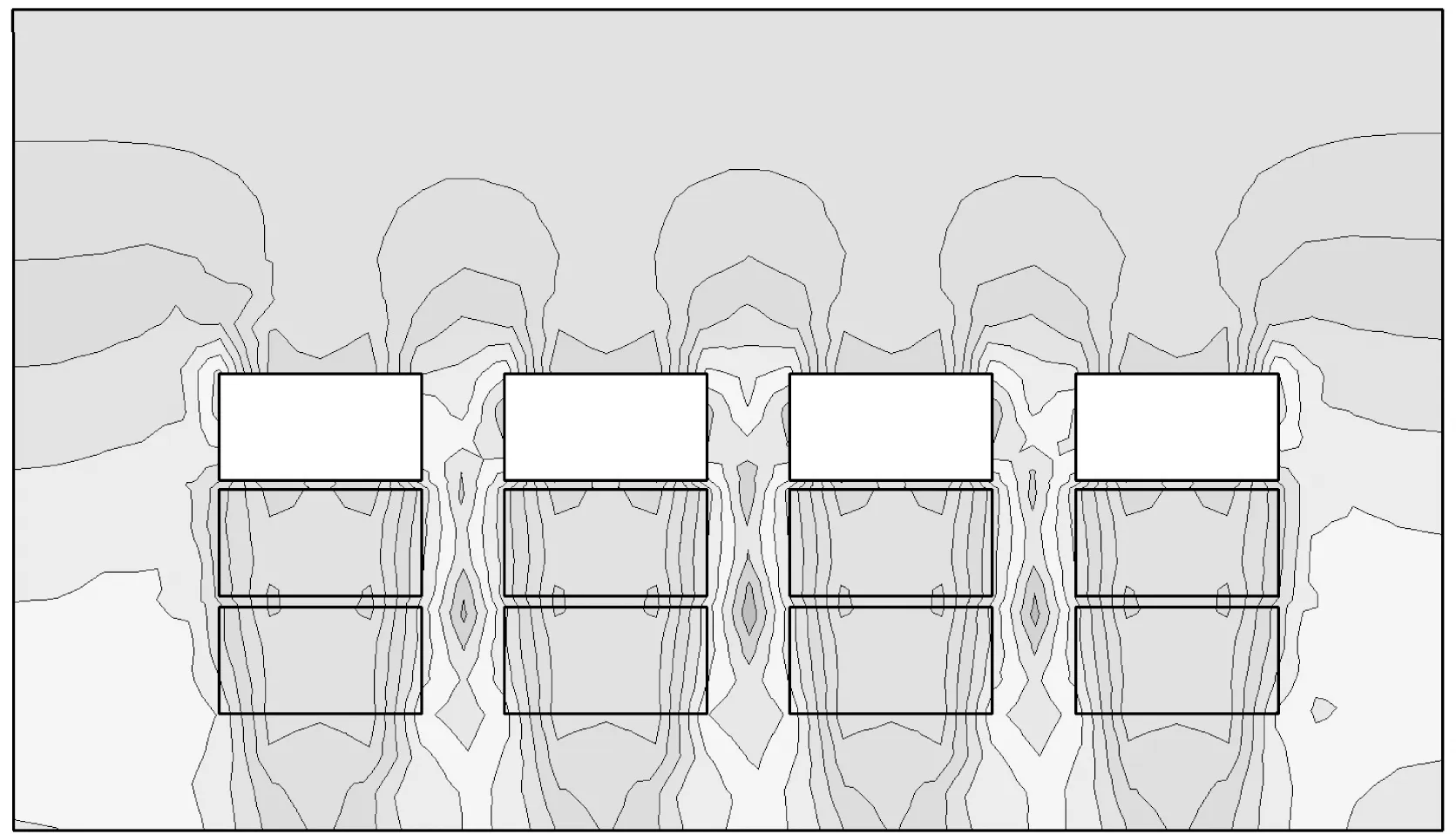
图5 采场正面的应力分布云图Fig.5 The stress distribution cloud map on the front of the stope

图6 采场侧面的应力分布云图Fig.6 The stress distribution cloud on the side of the stope

5 结论

1)对Mathews稳定图法进行改进，确定了上向分层充填采矿法矿房保持稳定的最佳跨度为18 m。

2)通过数值分析软件，对矿房进行数值模拟，并得出了与Mathews一致的分析结果。

3)采用Mathews稳定图法和数值模拟相结合的方法，先通过Mathews稳定图法初步得出采场结构参数，再使用数值模拟对多个采矿方案进行分析验证进而得出最佳设计，这一方法能够避免传统单一方法确定矿房跨度的缺点，在采矿设计时具有应用价值。