冰箱直线压缩机行程不稳定波动的机理分析

2

(1 中国科学院理化技术研究所 中国科学院低温工程学重点实验室 热力过程节能技术北京市重点实验室 北京 100190；2 中国科学院大学 北京 100049)

直线压缩机是由电磁系统、机械系统与热力系统相耦合的机电一体化装置，与控制系统和制冷系统一起构成典型的多变量耦合系统[1-3]。自由活塞结构使得直线压缩机不仅具有可通过调节行程实现变容量输出的特点，还易于出现行程跳跃或不稳定振荡现象[4-6]，这种不稳定振荡不仅影响系统运行性能，还极易导致压缩机活塞与机身撞击造成损坏而危害系统安全，稳定运行是保证直线压缩机可靠性的重要前提。

直线压缩机在低温制冷机、冷藏箱、电冰箱等小型制冷装置中已得到越来越广泛的应用[7-9]。制冷系统在扰动下也经常会出现诸如制冷剂质量流量、系统各处制冷剂压力和温度呈周期性波动的不稳定振荡[10-14]。当变容量线性压缩机与制冷系统相耦合时，二者之间的互相影响更突出，制冷系统的局部微小振荡可能会引起线性压缩机的不稳定振荡进而反向影响制冷系统的整体稳定性；同时线性压缩机的容量调节过程也可能会引起制冷系统振荡，并进而引发线性压缩机的不稳定振荡。在前期的直线压缩机冰箱系统启动实验中，开展了供电参数调节、电磁阀调节对直线压缩机运行稳定性影响研究[15]。如图1所示，在初始启动调节阶段，由于电压的反复调节产生了不稳定波动现象，随后在供电电压保持不变的过程中，行程幅值出现0.6 mm的周期性波动，一定时间后，此波动现象逐渐消失，当冰箱冷藏室温度达到设定值时，制冷系统电磁阀切换引起了相对较大的行程波动，约2.2 mm。对于其中供电调节和电磁阀调节引起的不稳定可以通过控制系统的优化设计实现规避。

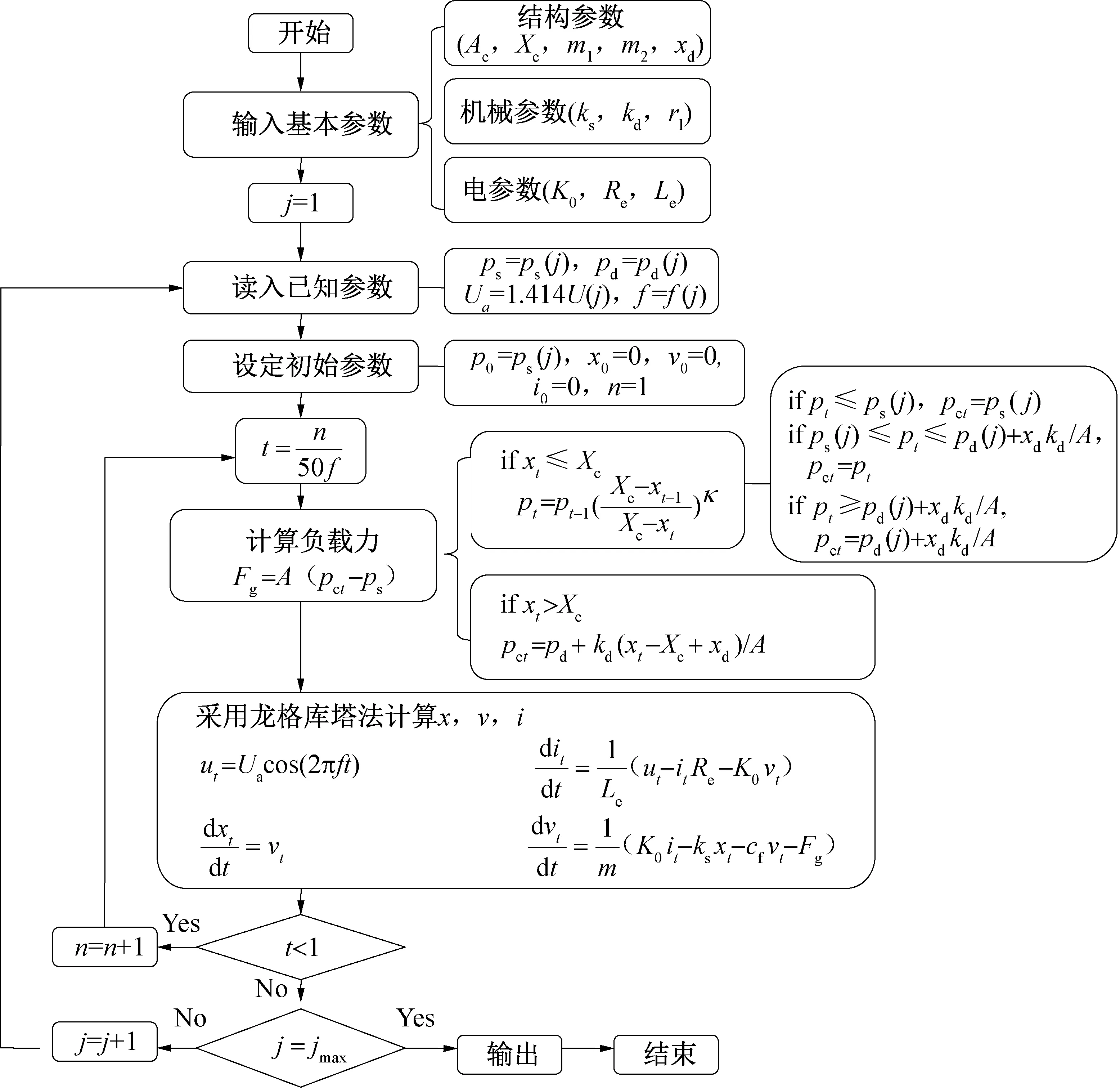
图2 直线压缩机动态运行仿真流程Fig.2 Flow chart of the numerical simulation of linear compressor

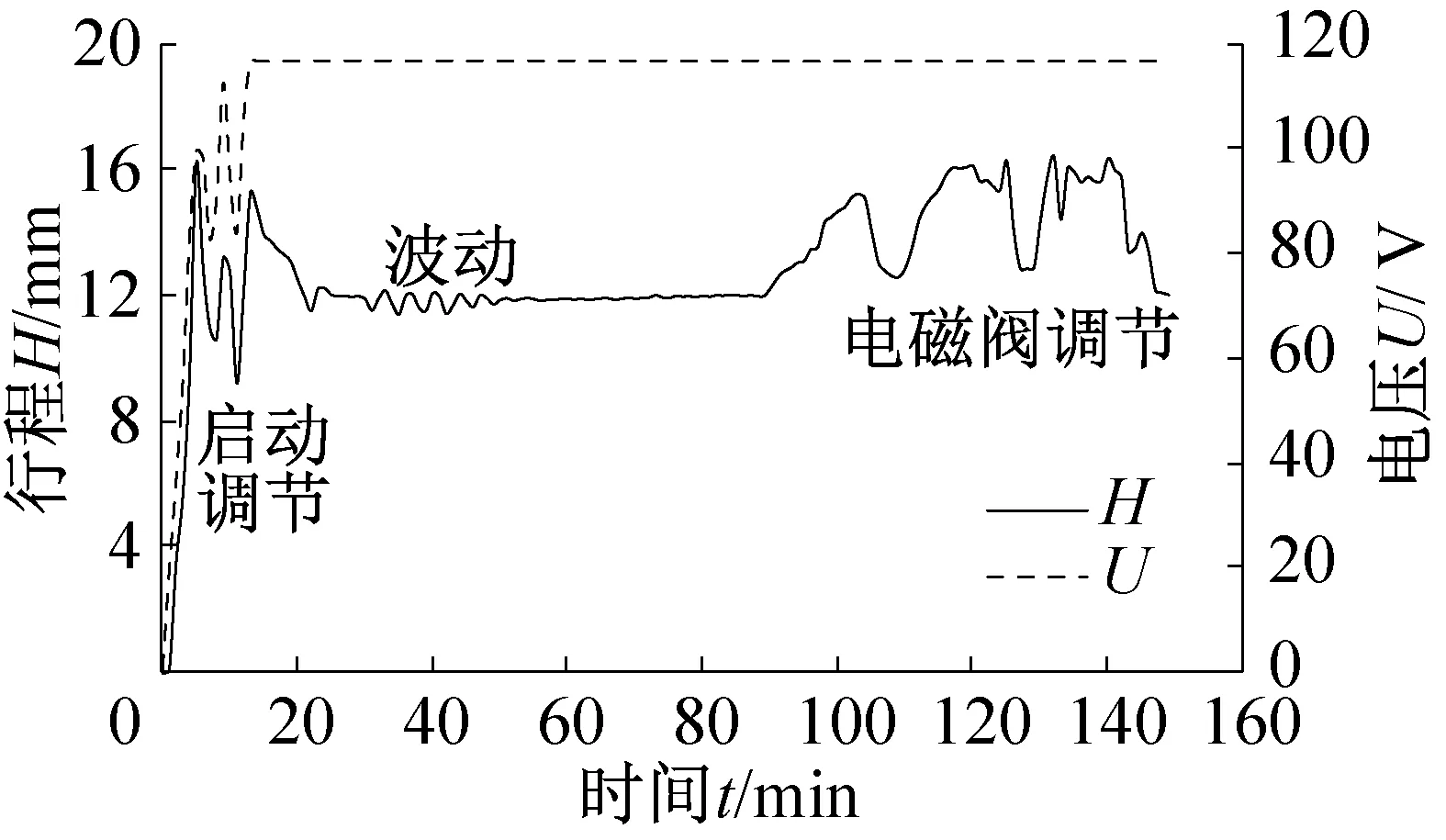
图1 直线压缩机不稳定启动过程Fig.1 Whole unstable start-up process of linear compressor

本文利用直线压缩机动态仿真模型，通过参数解耦，分析实验中第二段不稳定波动的发生机理，为避免直线压缩机在冰箱系统中出现此类不稳定现象提供理论依据。

1 理论模型与仿真建模

直线压缩机的活塞通过谐振弹簧与直线电机动子直接连接，在电磁场的作用下往复运动。其经典的动力学和电路耦合数学模型为[16]：

(1)

(2)

式中：m1为运动部件质量，kg；m2为机身质量，kg；cf为摩擦阻尼系数，(N·s)/m；ks为谐振弹簧刚度，N/m；Fg为气体力，N；x为活塞位移，m；u为电压，V；i为电流，A；Re为等效电阻，Ω；Le为等效电感，H；K0为电磁力系数，N/A。

负载力：

Fg=Ac[pct-ps]

(3)

根据式(1)～式(3)，可以建立基于MATLAB的仿真模型，仿真流程如图2所示。X为活塞位移幅值，m；Ua为电压幅值，V；Ia为电流幅值，A；fn为固有频率，Hz；ω为角频率；θ为电流电压相位差，(°)；Xc为静止时的活塞初始位置与上死点之间的距离，m；Xa、Xb分别为活塞往复振动时距离初始位置的位移，m；ps、pd分别为压缩机吸、排气压力，Pa；pt为压缩腔内压力，Pa；pct为活塞头压力，Pa；Ac为气缸截面积，m2；kd为排气阀弹簧刚度，N/m；xd为排气阀弹簧预压位移，m。模型中将直线压缩机的电压、电流、位移等参数设置为时变模型，根据实时吸、排气压力及活塞在气缸中的位移建立了压缩机负载力的时域模型，其中负载力模型考虑了吸气阀与排气阀的影响：当压缩腔内压力为pc>pd+kdxd时，排气阀打开；当活塞行程超过气缸头，接触到排气阀时，作用在活塞上的负载力为pdA+kdxd+kd(x-Xc)。

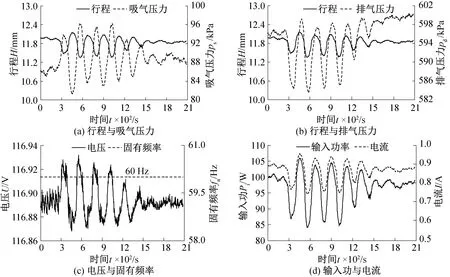
图3 测量参数变化曲线Fig.3 Change curves of measured parameters

输入基本参数包括结构参数、机械参数和电参数。除了结构参数决定于直线压缩机的结构设计，机械参数和电参数都可以通过实验测量结果确定。计算流程包括两个循环：内循环是根据输入的直线压缩机的实时吸、排气压力，供电电压及频率，初始设定t=0时刻的活塞位移、速度、电流及作用在活塞上的非线性负载力，采用龙格库塔法对压缩机位移，速度和电流这几个参数与气体力进行耦合迭代，得到它们的时域响应结果，并从时域曲线的峰-峰值获得活塞行程和电流有效值；外循环是用于工作状态变化的循环计算，计算不同工况条件下直线压缩机的运行响应结果。

2 分析与讨论

2.1 实验结果

图3所示为实验过程中测试的直线压缩机不稳定波动期间相关参数的变化曲线。由图3可知，此阶段的波动呈周期性变化，每个周期约为220 s，大约经历5个周期后，波动停止。图3(a)为波动期间直线压缩机活塞行程与吸气压力随时间的变化，随着活塞行程由11.97 mm逐渐减小至11.51 mm，最大波动率约为3.8%。吸气圧力逐渐增加到最大值，然后随着活塞行程的增加，吸气压力减小至最小值。图3(b)所示为活塞行程和排气压力随时间的变化，随着活塞行程的减小，排气圧力相应减小，行程减小至最小值时，排气压力降低至最低压力，然后随着活塞行程的逐渐增加，排气压力也逐渐增加至最大值。图3(c)所示为电压和固有频率随时间的变化。随着活塞行程的减小，固有频率逐渐增加，活塞行程达到最小值时，固有频率达到最大值，固有频率的波动范围为59.5～62 Hz，波动率约为5%。图3(d)所示为输入功和供电电流随时间的变化。可以看出，输入功、电流与活塞行程为同步变化，输入功率的波动范围为84.5～105.4 W，波动率约为21.3%。电流的波动范围约为0.76～0.95 A，波动率约为4.9%。

2.2 模拟分析

根据上述测试结果，将直线压缩机本体的结构、电气等参数、供电参数及吸气压力和排气压力数值读入模拟程序，并将活塞行程的模拟值与实验值进行对比(图4(a))，可以看出二者有很好的一致性。

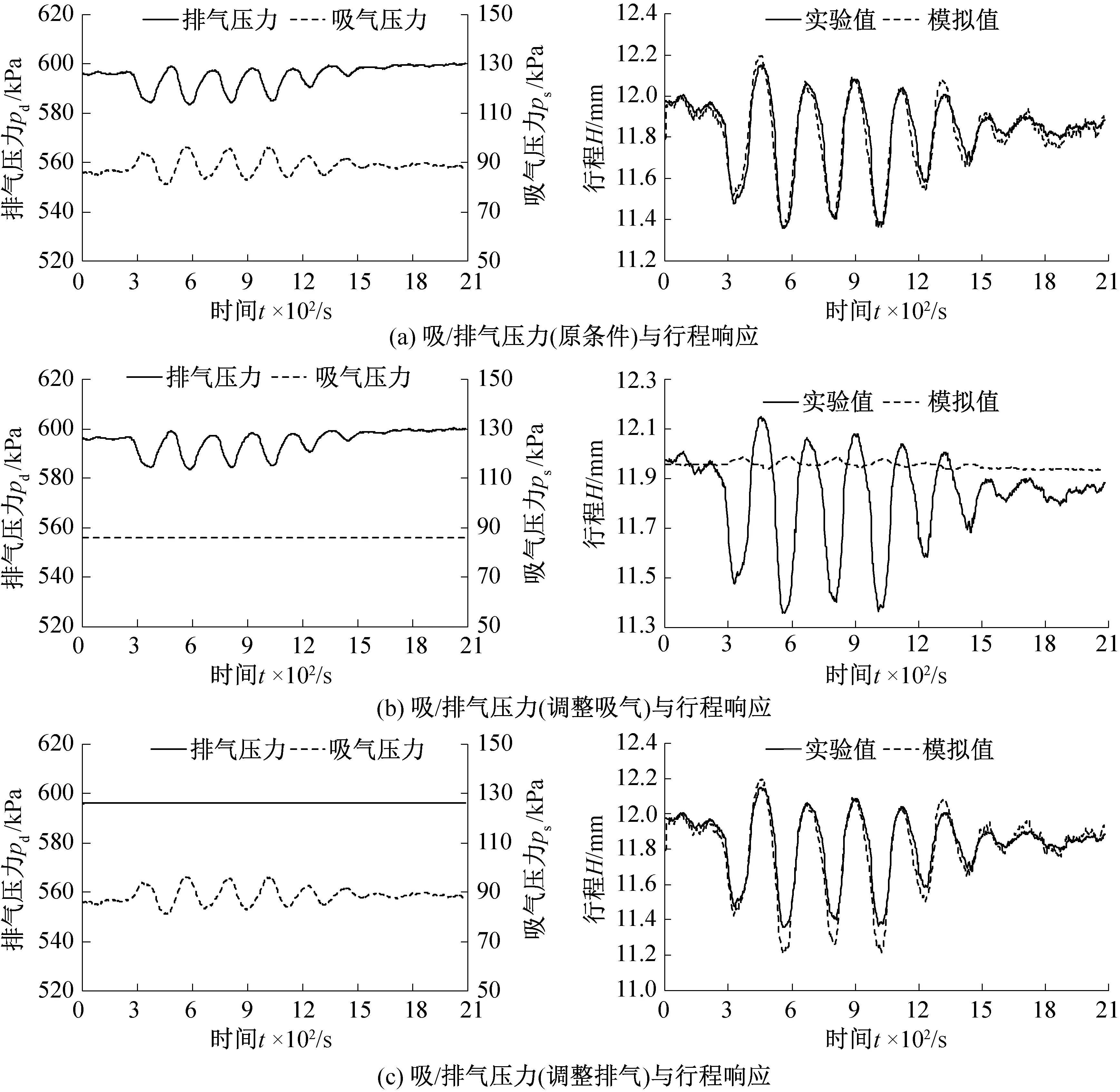
图4 模拟结果与实验结果对比Fig.4 Comparison between experimental results and simulated results

为了分析活塞行程不稳定波动产生的机理，这里采用参数解耦的方法来研究吸气压力和排气压力对活塞行程动态特性的影响。首先将输入程序的吸气压力调整为恒定参数，即波动周期中吸气压力的平均值ps=86 kPa，而输入的排气压力同实验结果一致，进行模拟计算，如图4(b)所示。可知在排气压力波动的作用下，行程波动约为0.05 mm，这说明排气压力的波动对行程波动的影响较小。进一步将输入程序的排气压力调整为波动周期的平均值，pd=596 kPa，输入的吸气压力与实验结果一致进行模拟计算，如图4(c)所示。可以看出，在吸气压力波动作用下,行程波动较大约为0.9 mm，与实验结果相差较小，说明吸气压力的波动是行程波动的主要影响因素。

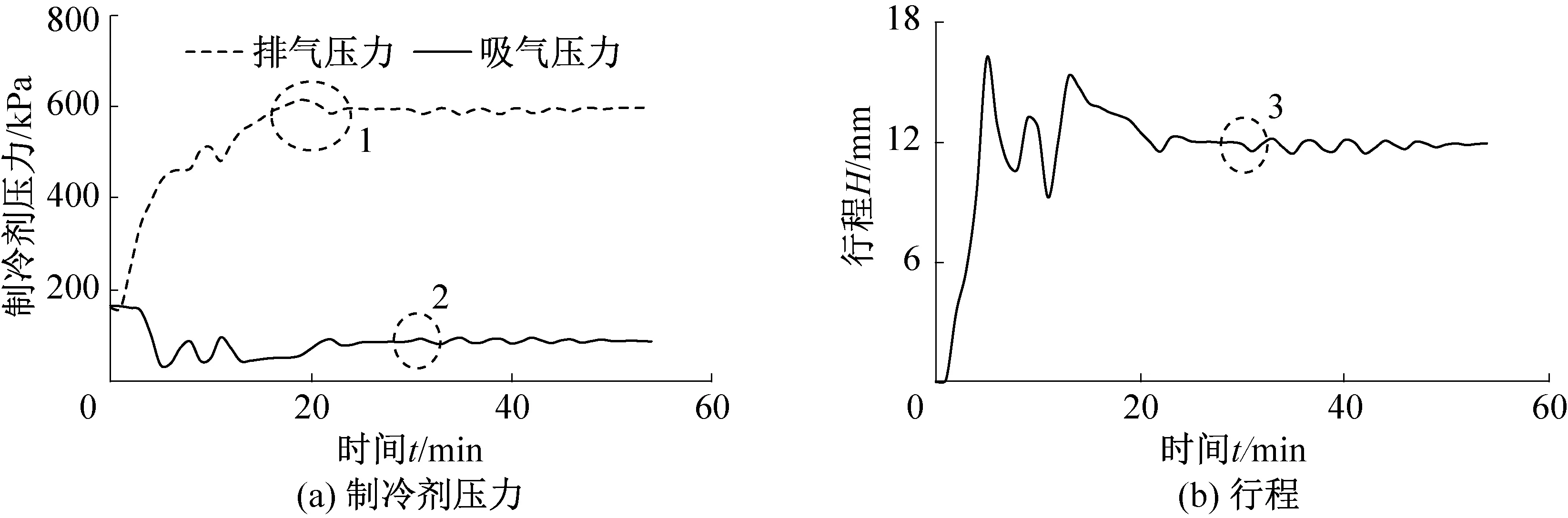
图5 不稳定波动发生机理Fig.5 Mechanism of the unstable fluctuation

通过上述模拟分析，可以对该不稳定波动的发生机理进行解释。如图5所示，在直线压缩机启动调节过程中，第一阶段调节过程中由于行程的剧烈变化，引起排气压力较大的增加(图中圈1内所示)。该波动慢慢从排气管道经过冷凝器、毛细管和蒸发器传递到直线压缩机的吸气段，引起吸气压力的增加(图中圈2内所示)。尽管直线压缩机供电参数未做任何调节，吸气压力的增加降低了活塞的行程，当吸气压力增至一定值时，活塞行程开始增加，行程的逐步增加又会降低吸气压力，从而使直线压缩机发生周期性行程的波动。由于这一阶段行程波动引起的排气压力波动较小，因而随着吸气压力和行程的相互制约，系统逐渐保持稳定。

3 结论

本文实验研究了直线压缩机冰箱系统启动运行稳定性。通过建立的直线压缩机动态仿真模型，对直线压缩机冰箱系统启动过程中出现的不稳定现象进行解耦分析，得到如下结论：

1)直线压缩机制冷系统的吸、排气压力的波动均对直线压缩机的行程响应产生一定的影响。相比于排气压力波动对直线压缩机行程的影响，吸气压力的波动对直线压缩机行程的影响更大。

2)直线压缩机启动过程中，供电参数的增减调节引起行程的波动，使排气压力产生较大的波动，该波动从排气端经一段时间的传递到吸气端，引起吸气压力的波动，从而引起直线压缩机行程发生周期性的波动。

3)保持供电条件不变时，吸气压力的增加使活塞行程减小，行程的减小导致吸气压力增加，二者互相影响互相制约，使系统逐渐保持稳定。