初中数学教学中学生创造性思维的培养

胡代兵

(湖北省仙桃市长埫口镇初级中学 湖北 仙桃 433000)

引言

教师应改变以往照本宣科的教学模式，从系统化的视角着手，课堂上预留时间允许学生自由的展开讨论，引发数学的激辩，事实证明，越是在轻松的环境中，学生的思维不受束缚，他们的数学感悟能力也就越强，对于知识的记忆和理解都会变得更加深刻，反而在教师主观臆测的情况下，不知不觉抑制了学生的思考意识，他们很容易形成思维定势，营造出自由的空间，使得学生更加热情的参与课堂的互动，潜移默化的激发学生的创造潜能。

1.创设问题情境，激发学生的数学创造性思维

学贵有疑，数学知识都是基于疑问的层面上，抽丝剥茧展开的内涵探究，将数学的内容层层揭示开来，更加透彻的去理解，更加积极的去分析，在问题上一石激起千层浪，引发学生的种种感悟。例如：教学“轴对称”时，教师先创设一个情境，利用相机将校园里面有轴对称的部分都记录下来，然后通过多媒体播放，利用幻灯片演示建筑、植物等，让学生去寻找其中的规律，然后教师提出疑问：“这些图片有哪些共同之处，用简洁的语言概括”，这样就引出了轴对称的概念，并了解了轴对称的性质，进而教师让学生从生活中找寻轴对称，动手操作利用纸张折叠成不同的轴对称图形，这样过程中就需要学生思维发散，大胆的去讨论和思考，折叠的方式不止一种，通过动手操作与思维碰撞，学生的创新意识迸发，同时看到其他学生的创新结果，能够给予学生更积极的动力，明确数学是没有标准答案的，需要他们去不断的摸索，在思考中衍生全新的感悟。

2.运用联想和猜想，培养学生的想象力

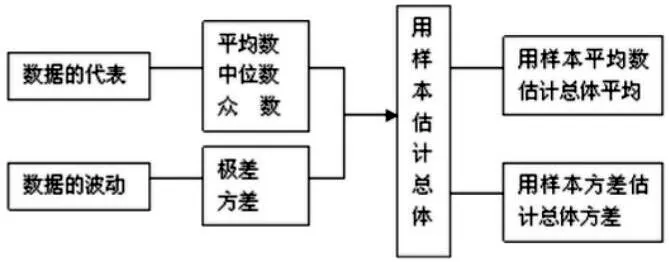
数学知识不断从未知到已知，从陌生到熟悉，这个过程中，学生通过灵动的思维去扫清知识的阻碍，通过想象将问题进行重组，强化学生的数感，在数学的联想和猜测中提高其创造能力。例如：教学“数据的分析”时，我们可以通过联想的形式，将平均数、中位数、众数分别比作不同种类的人，通过大胆的联想，将这些容易混淆的概念，以思维导图的形式搭建出结构框图，学生脑海中接受到的知识不仅都从静止转化为灵活动态的场景，还能够在图示模型下，整合成系统的概况，此时学生的思维变得十分活跃，他们不拘束于知识本身，而是超脱知识的限制，梳理清楚了知识的概念，对于相应的问题解答也就水到渠成。

3.突出数学思想与方法渗透

初中时期虽然数学的知识较为繁杂，但其思想是多样性的，不同的问题中借助类似的思想与方式，都可以互相联通，挖掘隐藏的数学知识信息，从而使得基础得到夯实，这也是数学推理的重要环节，有助于学生创新联想，解决数学的难题，形成内心的满足。数学的思想总结起来有：整体思想、数形结合思想、转化思想、由特殊到一般的思想、方程思想、类比思想等，整体的思想就是在集成化的思维模式下，将有关的图形、数据都整合起来，综合的进行讨论，这样在代数式的化简、求值上，都可以得到广泛的应用，获得数学的正解。数形结合是较为常见的一种抽象变直观的教学手段，与转化思想有着异曲同工之妙，解答特殊问题时，将其归纳为一般思路，也可以逆向思考，将一般的问题化为较为特殊性的情境，这样在思考问题时，就有一定的方向可循，方程思想应用于方程类的问题上，是应用题一题多解的基础条件，类比将有关的内容对照比较，通过之间的关联性进而找到其化解的要点。这些都是学生数学求知中必备的学习技巧，也是衍生创新性思维的契机。

4.充分挖掘教材，注意知识的发现过程

学生应了解知识的形成过程，而不仅仅了解知识浅层面的信息。例如：教学“分式”时，教师出示案例：9x+4,7/x,9+y/20,m-4/5……判断哪些是分式，哪些是整式，了解分式中x取何值时，分式有意义，从基础入手，进而去明晰分式的相关内涵，再展开应用题的辨析就简单的多。

结束语

综上所述，初中数学的创新思维培育过程中，教师可通过知识的内在挖掘、数学的思想技巧了解、数学的思维联想、情境的构建等模式，让学生充满创造激情，在创造意识中强化理解。