基于状态图测试的迁移路径生成方法*

张毅伟，贲可荣

海军工程大学 电子工程学院，武汉 430033

1 引言

随着软件产品的普及及其需求的多样化，软件的复杂性也不断增加。如何提高软件质量是软件工程致力于解决的关键问题之一，软件测试是提高软件质量最重要的手段。随着面向对象软件开发的应用以及自动化测试的需要，基于模型的软件测试（model-based software testing）[1]越来越受重视。它无需系统结构的内部信息，而是使用系统规范来派生测试用例。通常使用模型来建立一个系统规范[2]。

软件工程的发展演变也由传统的模式化转向智能化。基于搜索的软件工程（search based software engineering，SBSE）是传统的软件工程与智能计算交叉的新的研究领域。它从实际问题的解空间出发，采用元启发式搜索优化算法，以适当的计算开销来解决可转化为优化问题的软件问题。基于搜索的软件工程已在软件工程领域取得了显著的研究成果，尤其是在软件测试方面的应用得到了更多的关注，促进了软件测试的发展。在此背景下，本文针对UML（unified modeling language）模型中依赖迁移难覆盖的问题，提出一种改进的分组遗传算法（improved grouping genetic algorithm，IGGA），把UML状态图中的迁移关系、变量等作为启发式信息，搜索生成可执行的迁移路径。对算法的编码方式以及适应度函数进行设计，引入自适应算子以及模拟退火机制，实验结果验证了本文方法在生成迁移路径覆盖率和生成效率方面的有效性。

2 研究背景

2.1 相关概念

为了解决装箱问题（bin packing problem，BPP），Falkenauer提出了分组遗传算法（grouping genetic algorithm，GGA）[3]。BPP是一个非确定性多项式难分组问题，需要将各种尺寸的物品在固定容量的箱子内进行分组，并且需要尽可能地利用箱子内的空间。GGA是一种将原本呈一列的染色体进行分组处理以适合分组问题结构的一种遗传算法。GGA与传统遗传算法（genetic algorithm，GA）有两方面不同。

（1）为使分组问题的相关结构成为染色体中的基因，GGA使用了特殊的编码方案。个体中的小组都是有意义的组成部分，能够表示关于它们所属解决方案的预期质量信息的最小部分。GGA中染色体表示如下：

[(2 7)(3 8)(1 9)]

（2）鉴于编码方式的不同，需要使用适合染色体的特殊的遗传算子。选择运算使用比例选择算子，遗传的可能性与个体适应度的概率成正比。交叉操作则是在被选择的个体中随机选择两个个体作为交叉对象，在染色体的分组间随机产生交叉点，将一条染色体中两个交叉点之间的基因插入到另一条染色体中。变异运算的实现取决于面临的问题，Falkenauer提出的变异操作分为三种：创建一个新分组、删除一个现有分组、将少量基因在分组之间进行置乱。

基于UML模型的测试是基于模型软件测试的一个重要方向。在软件开发的各个时期，都能使用UML进行设计，得到规格说明和测试需求来实现测试的执行。基于模型的测试覆盖准则可以分为[4]：面向控制流的、面向状态或迁移的。迁移覆盖常被作为准则来衡量测试的充分性[5]。一条迁移路径（transition path，TP）是从状态图的初始状态开始的一系列迁移[6]。若一条迁移路径中的迁移都能按照顺序被触发执行，这就是一条可执行的迁移路径（feasible transition path，FTP）。

状态图中的迁移有时会涉及程序中的变量，且变量的值会影响到后续迁移的走向。变量的值由迁移中的行为改变。这样的一组迁移就被称为依赖迁移组（dependent transition group，DTG）。DTG的存在会导致迁移路径的不可执行。例如迁移a中的动作是i++，迁移b的守卫条件是i≥5，若迁移a的执行不足5次的话，就难以触发迁移b的执行。这会使得迁移路径不能按照输入序列来执行，导致覆盖率的下降。因此本文考虑将分组遗传算法应用于可执行迁移路径的生成中，并针对具体问题的特性将算法进行设计调整。

2.2 相关工作

针对基于模型的测试，已经有多种方法被用来生成迁移路径。Kalaji等人[7]使用传统遗传算法生成迁移路径，提出了一种基于搜索的集成方法，用于EFSM（extended finite state machine）的自动化测试。该方法分为两个阶段：第一阶段使用适应度函数基于数据流依赖可行性度量的遗传算法，来产生可行的TP；第二阶段使用适应度函数基于分支近距离函数的遗传算法来搜索能够触发TP的输入序列。但是该方法因为破坏了DTG而导致了路径的不可行。Hierons等人[8]认为路径中存在的过渡行为通常会导致不可行的路径。并提出了一种绕开DTG，通过在遗传算法中使用评估方法来指导搜索FTP，但是该方法仅能在涉及简单迁移变量的状态图中适用。Li[4]提出了统一的路径覆盖准则体系和面向程序中罕至部分、重点区域和特定目标组的符号执行制导策略。该方法能够针对不同程序取得较好的效果且能有效提高搜索效率。Choi等人[9]将GGA用于迁移路径的生成，通过对不同系统的实验取得了较高的迁移覆盖率。Wu等人[10]提出一种面向路径的可执行迁移路径生成方法，该方法所生成的路径能覆盖被修改影响的节点。Jungsup等人[11]提出了一种可重用的通用软件平台，该软件框架不仅提供设计模式来查找目标模型的测试用例，还使用常用功能来缩短开发时间，但是在生成FTP方面，提出的新测试框架难以覆盖存在DTG的区域。

GGA已经被用在许多领域来解决有关分组操作的问题。Chen等人[12]应用GGA开发了一种机器选择模型，来解决并行机床柔性作业车间调度问题。Salcedo等人[13]将GGA的遗传算子进行改进并将其用于解决聚类问题，取得了比传统方法更好的效果。GGA解决的问题中均包含可以分组的元素，状态图中可执行迁移路径的生成也具备该条件。本文借鉴Falkenauer[3]和Choi等人[9]的思想，针对DTG区域难覆盖的问题，提出一种用于生成迁移路径的改进分组遗传算法（IGGA）。

3 改进的分组遗传算法

本章介绍将分组遗传算法（GGA）进行改进的方法。本文方法主要是针对具有DTG的状态图，对其他状态图同样适用。下面通过一个具体的状态图（如图1所示）说明算法的改进工作。GGA具有通过分组来进行交叉操作的特性，需要把特定的标记作为分组保护起来。基于模型的测试能够在一个DTG上收集数据，然后在一个分组里面将DTG绑定。以下针对本文涉及问题的特性，对GGA进行改进。

Fig.1 Example of state diagram图1 状态图示例

3.1 个体编码

利用遗传算法对实际应用问题求解时，需要通过编码将问题的解空间转换为遗传算法的搜索空间。本文采用对整数表示的迁移路径进行分组编码的方式，进化的个体为若干迁移路径组成的集合。其中迁移路径的数字表示在生成迁移信息表之后用整数对所有的迁移依次标注。基于顺序的表示被用作解决可执行迁移路径生成问题的染色体的表现形式。染色体中的基因对应于经过的迁移。个体的编码如图2表示。

Fig.2 Chromosome encoding method图2 个体编码方式

个体被分为数个小组，小组中包含基因。用迁移路径的序号表示路径，有利于降低个体编码的复杂度[14]。本文提出一种原始基因的方式来保护可执行迁移序列。初始化染色体之后，分组中创建一个原始基因，原始基因不会被改变。如图2中三角形所指，首先放置的原始基因被指定为小组号。

当进行遗传操作时，原始基因将会和与它们相联系的迁移组织在一起。相同组号的分组极有可能包含相似的基因。对不同的小组设置组号，由不同的组号标记染色体中的分组来保持基因的多样性，有助于提高迁移覆盖率。原始基因在分组被淘汰前将一直存在个体中并且引导个体分组进化的方向。

3.2 初始化算法

种群初始化过程创建了一个染色体相互作用的环境，产生与设定种群大小相同的初始化染色体。本文考虑优先将DTG插入小组。初始化从随机插入基因开始。最先插入的基因为原始基因，记作t′。

若t′的守卫条件中包含内部变量，则t′就是受影响的迁移。在状态图中搜索另一个包含动作能够满足t′守卫条件并产生影响的迁移，记为t。搜索到t之后，则分析t中包含的动作和为了到达t′所需要经过t的次数，并在染色体内添加所需次数的t。若t′不存在依赖的迁移t，则此过程中就不添加新基因。搜索t的过程如图3所示。搜索t从第一级的迁移集合tn1中选择直接连接到t′的迁移开始。从tn1中寻找的t要包含动作来满足t′中的条件守卫。如果在tn1中没有找到t，连接到下一级的迁移集合tn2中的迁移就作为备选。以此类推，整个搜索过程不断深入直至找到t。

种群初始化流程如图4所示。初始化过程中用到的状态图信息有迁移总数、迁移集合、迁移信息表、输入个体中的基因个数、种群规模。添加产生影响迁移t的完成标志着迁移搜索阶段的结束，随后在小组中添加随机基因，直到达到个体的初始长度。个体的初始长度为状态图中的迁移总数，与达到迁移全覆盖的最短可执行迁移路径的长度一致。

Fig.3 Search process of generating dependent transition图3 产生依赖迁移搜索过程

3.3 适应度算法

Fig.4 Flow chart of population initialization图4 种群初始化流程图

适应度是个体对环境的适应程度，它取决于遗传特性。适应度函数的设计包括建立一个问题的目标以及定义必须被满足的元素以判断染色体是否接近最优解。通常需要选取相应的覆盖策略来衡量测试的充分性。本文使用迁移覆盖准则。迁移路径要尽可能覆盖更多的迁移。本文研究的适应度函数主要考虑个体满足状态图迁移覆盖的程度，基因的关联性也占一定权重，不具备关联性的迁移路径将无法执行。关联关系检测主要是检查下一次迁移的源状态和上一次迁移的目标状态是否相同。若不一致，则被视为迁移路径中间断开，适应度值随之降低。在针对DTG的迁移覆盖判断前需要对路径可行性进行检查，其中涉及到迁移信息表。

适应度函数如式（1）～式（3）所示：

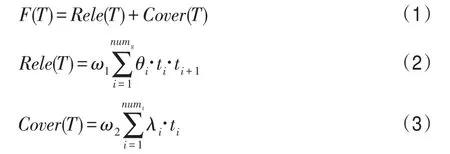
式中，ω1、ω2表示权重，ω1>ω2，θ,λ∈[0,1],θ,λ∈Z，θ表示基因间的关联性，λ表示迁移是否被覆盖，ti表示迁移i，具体评价个体适应度的流程如图5所示。图5中的fitness增加按照适应度函数进行，种群进化中个体的适应度值包括两方面：

（1）某个体覆盖迁移越多，则适应度值越大；

（2）某个体中基因所代表迁移间的关联性越好，则适应度值越大。

Fig.5 Flow chart of fitness evaluation图5 适应度评价流程图

3.4 遗传操作算子

种群中的染色体通过遗传算子来实现相互作用。获得最优解的速度很大程度上依赖对问题设计遗传算子的准确性。现有的分组遗传算法不适用于解决可执行迁移路径的生成问题。本节针对研究内容设计选择、交叉、变异和修补四种遗传算子。

3.4.1 选择算子

选择算子用来确定进入下一代的个体，以及产生子代个体的数量。选择是一个基于适应度值的操作，适应度值越高的个体被选择的概率更大。本文采用轮盘赌法和最优保留机制来选择种群个体。个体传递到程序中运行，由适应度函数得到适应度值。按适应度值将个体由大到小排列，选取一定比例的大适应度个体直接加入下一代种群中。剩余个体被选中的概率与其适应度值成正比。numns表示种群中未被选中的个体数量，T表示未被选中的个体，F(T)是适应度函数，T被选中遗传到下一代群体的概率如式（4）所示：

3.4.2 交叉算子

Fig.6 Process of crossover图6 个体交叉过程

为了提高种群多样性，算法的收敛性以及避免形成局部最优，本文引入了改进的动态自适应交叉算子[15]，个体两两发生交叉的概率如式（5）所示。

其中，pc1>pc2，f是需要交叉个体的较高的适应度值，fmax是剩余个体中适应度的最大值，favg是种群适应度的平均值。通过这个过程，交叉后的个体中将不存在相同组号的小组，个体可以确保相同基因的重现。交叉后个体的长度问题，将用后文中的修补算子加以限制。

3.4.3 变异算子

交叉操作形成了新的子代个体。若父代个体在某交叉区域内的小组号均相同，则不能产生新的基因型。变异算子是对个体的基因进行变异，从而产生新的个体。Falkenauer提出了3种变异方法，本文将变异操作设计为淘汰已有小组。

按照一定概率选择作为变异目标的个体随机地选择并删除其中的一个小组。但是当个体中小组的数量少于3个，变异后个体的交叉点形成不了交叉区域且会降低个体的多样性。故个体中组数少于3个就停止变异操作。与交叉算子类似，本文在设计变异算子时也引入改进的自适应变异算子，个体发生变异的概率如式（6）所示。

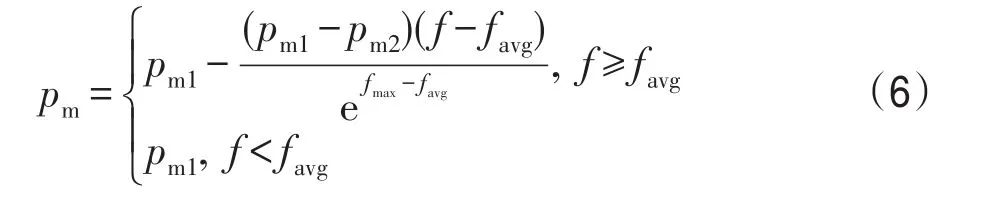
对于交叉、变异之后个体，本文应用模拟退火算法来接受。当产生新个体P′T时，接受其的概率由Metropolis准则确定[16]：若新个体的适应度更高，则接受新个体；否则以一定的概率接受质量并未提高的新个体，其概率计算如式（7）所示：

式中，fk+1是新个体的适应度值；fk是原个体的适应度值；tk+1是该算法中的温度条件控制参数；ptk+1

是接受概率。

3.4.4 修补算子

针对不同的状态图，满足迁移覆盖的迁移路径的长度不同。迁移的重复执行也可能导致个体长度的不断增长。选取一个长度值Len对个体进行限制。若交叉、变异操作后的个体长度与Len不一致，则需要对个体进行修补，具体如算法1所示。

算法1修补算子

输入：染色体中基因数numg、染色体中小组数numgp、个体长度限制Len。

输出：修补后的个体chromosome。

长于Len的个体，先删除与前后不关联的基因。若基因均相关，则随机删去一个小组。虽然基因是相关联的，但是由于已覆盖路径的重插入，导致个体很长却不能确保覆盖率。组号不同的小组可能覆盖了相同的区域。为此本文采用一种在删除完成之后，随机删除分组的修补方法。删除一些已经存在的分组能够为新元素腾出更多的空间，让染色体中的小组能够覆盖不同的区域。短于Len的个体，寻找不关联的基因，并在一个基因之后加入能与其相关联的基因。若基因均关联，则在个体末尾加入关联基因，直至长度达到Len为止。

以上是本文对GGA的改进，将迁移编号作为基因并为每个小组设置组号，通过组号的异同判别个体是否覆盖相同区域。通过搜索状态图的原始信息初始化种群。评价适应度时考虑覆盖率与关联关系两项，给出了适应度函数公式。将轮盘赌法与最优保留机制结合来选择个体，利用GGA不同的交叉变异方式进行遗传操作，引入自适应的遗传算子以及模拟退火的接受机制以提高求解速度，最后针对个体的长度问题提出了相应的修补算子。

4 迁移路径生成

由以上改进的算法，可以得出基于IGGA的可执行迁移路径的生成框架，分为状态图分析模块和算法模块。状态图分析模块是对图的迁移结构进行分析，生成3.2节、3.3节中提到的迁移信息表。以图1为例，迁移信息表如表1所示。

Table1 Information of transitions表1 迁移信息表

每一次迭代以后都会产生新个体作为下一轮迭代的初始种群。需要的迭代次数通常意味着算法优化的收敛状态。算法模块根据迁移信息表进行相应的操作。本文是以生成的符合条件的染色体为最优解，同时以是否达到算法预定的最大迭代次数为终止条件。基于IGGA算法生成可执行迁移路径具体的流程步骤如图7所示。

Fig.7 Flow chart of FTP generate based on IGGA图7 基于IGGA的可执行路径迁移生成流程图

具体步骤如下：

步骤1由状态图生成迁移信息表。

步骤2设置初始化的参数，包括种群规模、最大遗传代数Gen、交叉概率pc、变异概率pm等参数。

步骤3由3.1节所述的编码方式和3.2节所述的初始化方法，产生初始种群Pop。

步骤4使用3.3节中的算法计算适应度值。

步骤5检查是否满足终止条件：个体适应度值为(Len-1)ω1+ω2Len或是达到设定的遗传代数，若满足条件，则转到步骤10。

步骤6对种群中个体按照3.4节中的方法进行选择。

步骤7对剩余个体使用交叉和变异算子进行自适应的交叉和变异操作。

步骤8将新产生的个体根据3.4节中所提操作修补至长度Len，产生新的种群集合Pop′。

步骤9重复执行步骤4至步骤8，若达到一定遗传代数Gen，则Len+1，并进行下一轮迭代。

步骤10停止遗传操作，输出满足的个体及其覆盖率。

5 实验与分析

为分析讨论算法参数和验证算法的有效性，本文的实验分为两部分：5.1节以inres initiator协议和ATM两个系统为例，比较本文设计的算法与文献[7]、文献[9]、文献[11]中方法在生成可执行迁移路径（FTP）上的覆盖率；5.2节通过比赛判定系统（game winner check，GWC）、警报系统（alert system，AS）、错误等级检测系统（fault level check，FLC）三个状态图为例，与文献[9]中方法比较生成同样数量的FTP所需要的遗传代数，通过结果分析本文方法的性能，观察其在加快求解速度方面的效果。

文中进行的实验程序使用Matlab语言编写，并在MatlabR2015a中运行。实验的硬件配置为2.50 GHz Intel®CoreTMi5-3210M CPU、4 GB 内存，安装了Microsoft Windows 7 32 bit操作系统的计算机。

在进行上述实验之前，本文引入文献[16]中状态图的结构复杂度对于状态图理解的影响来分析每一级个体长度搜索代数的因素。其使用状态图中的简单状态的数量（number of simple state，NS）、圈复杂度（cyclomatic complexity，CC）、迁移的数量（number of transition，NT）来定量表示状态图结构的复杂度，圈复杂度定义为|NS-NT+2|[17]。本文将元素分别设置为实验组和对比组，观察其对搜索代数的影响。在实验结果的基础上，对于某一状态图，所需要的遗传代数Gen可以近似表示为式（8），其中α是比例权重。在总体流程中，若某长度Len的个体搜索满Gen次，则将个体长度Len+1，并进行下一个迭代周期。

本文还研究交叉概率pc、变异概率pm、种群大小Popsize对于总的遗传代数G以及个体长度Len的影响，并得出针对示例状态图的最优遗传参数。

5.1 算法覆盖率实验分析

为了验证本文算法生成FTP的有效性，本节将以inres initiator协议和ATM两个系统实例，将本文算法运行结果与文献[7]、文献[9]、文献[11]中方法的结果作比较。两个系统的状态图如图8和图9所示。为了简化，原图中的事件均用en表示，迁移用tn表示，只表示出涉及依赖迁移组（DTG）的守卫条件和行为。inres initiator和ATM是典型的包含DTG的系统。ATM状态图中，t2、t3、t4包含变量attempt的判别条件，t2中包含引起变量attempt值变化的行为，故t2、t3、t4构成了DTG。inres initiator协议状态图中，t3、t8、t10包括变量counter判别的守卫条件和变量counter加1的行为，t4、t9、t11中包括变量counter的判别守卫条件，故t3、t4、t8、t9、t10、t11构成了DTG。实验所取的遗传参数如表2所示。

Table2 Genetic parameters of experiment表2 实验所取遗传参数

在上述两个系统UML模型的基础上，利用给定的遗传参数生成可执行的迁移路径，4种方法的区别在于：文献[7]使用原始的遗传算法（GA）；文献[9]使用分组遗传算法（GGA）；文献[11]采用一种新的测试框架MISF（model-independent software framework）；本文采用改进的分组遗传算法（IGGA），并引入自适应遗传算子与模拟退火接受机制，生成迁移路径的覆盖率如表3所示。

Table3 Comparison of transition path coverage表3 生成迁移路径覆盖率结果比较

由表3可以看出，对于上述两个系统状态图使用本文方法能够达到100%的迁移覆盖，相比于使用传统遗传算法分别提高了4.16%和25%，相比于使用MISF分别提高了20.48%和33.33%，与采用GGA的覆盖率持平。本文使用的IGGA将DTG保护在个体的遗传分组中，使得其依赖关系不被破坏，从而能够达到难覆盖的迁移路径。使用GGA的种群规模均是80，本文使用IGGA时，种群规模分别减小了25%和12.5%，说明IGGA能够在缩小种群大小的前提下达到相同的迁移覆盖效果。本节实验中IGGA与GGA达到的覆盖率效果相同，将在5.2节中实验分析比较本文的IGGA与GGA在生成迁移路径时所需代数等方面的差别。

Fig.8 ATM state diagram图8 ATM系统状态图

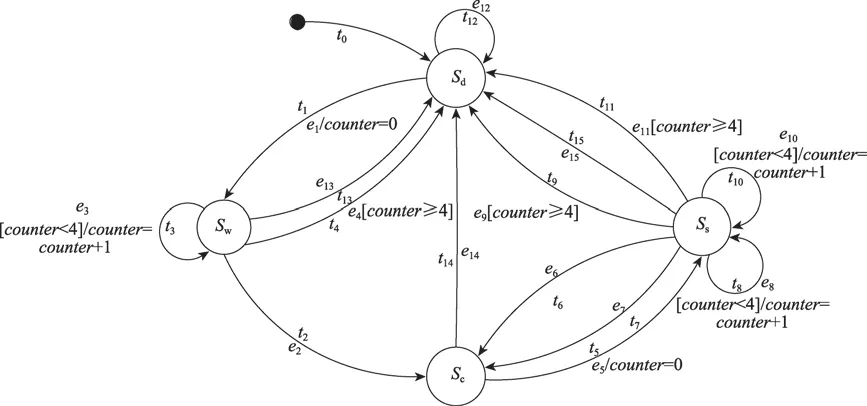
Fig.9 Inres initiator system state diagram图9 Inres initiator系统状态图

5.2 算法性能实验分析

为验证本文改进遗传算法的性能，本节以文献[9]中的比赛判定系统（GWC）、警报系统（AS）、错误等级检测系统（FLC）三个状态图为例，比较IGGA和GGA在生成迁移路径时的收敛速度。上述三个系统状态图如图10～图12所示。同样依照前文所述方法，所取的遗传参数如表4所示。本节的三个系统状态图均包含依赖迁移组，且其中依赖变量的值在不断增大，这也使得生成可执行迁移路径的难度逐渐变大。

根据表4的遗传参数和采用文献[9]中的实验规模进行实验，对每个状态图生成500条迁移路径。实验结果比较如表5所示。

由表5可以看出，对三个系统状态图进行实验，本文方法由于引入了自适应的遗传算子和模拟退火的接受机制从而加快了收敛的速度。在生成相同数量可执行迁移路径的前提下，所需的迭代次数分别减少了14.33%、16.41%、19.66%，生成的迁移路径长度基本相同。另外，从这个结果也可以看出对于难覆盖的迁移路径越长的系统状态图，本文方法求解速度的提高也越明显。综上所述，使用IGGA生成迁移路径的方法无论是在迁移覆盖率还是种群规模都具有优势，引入的自适应遗传算子和接受机制有效加速了算法的优化进度，使其具有更好的寻优性能。

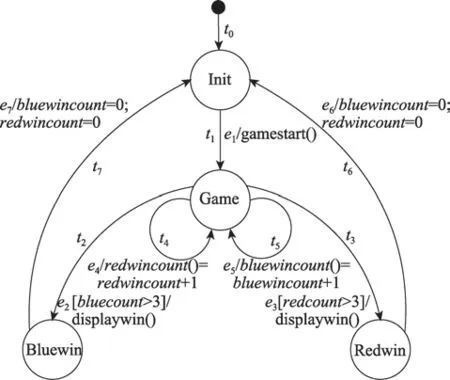
Fig.10 GWC system state diagram图10GWC系统状态图

Fig.11 AS system state diagram图11 AS系统状态图

Fig.12 FLC system state diagram图12 FLC系统状态图

Table4 Genetic parameters of experiment表4 实验所取遗传参数表

Table5 Comparison of experiment results of transition path表5 生成迁移路径实验结果比较

6 结束语

本文利用分组遗传算法中分组的思想将依赖迁移组归到一起，通过对编码方式和适应度函数的设计，使得生成的迁移路径能够覆盖依赖迁移组。引入了自适应的遗传算子并用模拟退火机制接受交叉后的个体，对每次迭代后得到的个体进行修补，使其满足搜索规则。实验分析了状态图结构对遗传代数的影响，讨论了遗传参数对算法性能的影响，对比实验验证了本文方法达到了迁移覆盖的有效性，结果表明本文方法能够在生成相同数量可执行迁移路径的前提下缩小种群规模及迭代次数，具有更好的寻优性能。

本文进一步的工作是能否引入新的搜索策略，进一步提高效率，如何自动生成相应的测试数据来触发迁移路径的执行，将本文方法通过参数调节等方式应用于除考虑事件之外的更加复杂的情形。这些也是基于模型自动化测试中需要继续研究的内容。