Spin squeezing in Dicke-class of states with non-orthogonal spinors

K S Akhilesh,K S Mallesh,Sudha,and Praveen G Hegde

1Department of Physics,University of Mysore,Manasagangotri,Mysuru-570006,Karnataka,India

2Department of Physics,Kuvempu University,Shankaraghatta,Shimoga-577 451,India

3Inspire Institute Inc.,Alexandria,Virginia 22303,USA

Keywords:Majorana representation of pure symmetric multiqubit states,spin squeezing,Dicke states

1.Introduction

Spin,an intrinsic degree of freedom of the physical systems is a fascinating area of study as it is entirely of quantum origin not having a classical analogue.The componentsof the spin operatorare non-commuting and hence obey the uncertainty relation

Based on the uncertainty relation satis fied by position,momentum operators,the concept of squeezing was first introduced for the states of harmonic oscillator and it was later extended to the radiation fields.[1-3]A comparison of the uncertainty relation satis fied by the components of spin operatorwith that of the non-commuting operators of bosonic systems led to the extension of the concept of squeezing to spin systems.[4]In the case of spin systems the lower bound which is essential for the study of squeezing needs a careful consideration because of its coordinate dependence.This led to the conclusion that the behaviour of squeezing is dependent on the choice of the coordinate frame.Kitegawa and Ueda[4]showed that the occurrence of squeezing in spin s state is due to the existence of quantum correlations among the constituent 2s spin 1/2 systems and suggested a coordinate independent definition of spin squeezing.According to Kitegawa-Ueda,[4]an N-qubit state is KU spin-squeezed if the minimum variance of a spin component normal to the mean spin direction is smaller than the standard quantum limitof the spin coherent state.Thus,for a spin squeezed state,and hence the Kitegawa-Ueda spin squeezing parameter is defi ned as,

where ξ is a quantitative measure of spin squeezing and for a spin squeezed state 0≤ξ＜1.

Spin squeezing has been an intense area of study[4-26]due to its theoretical importance as well as the applicability of spin squeezed states in the fields of low noise,high precision spectroscopy[27-29]and quantum information science.[10,11,13-16]The relative ease with which spin squeezed states can be produced,[10,26]has made them more accessible and hence useful in the concerned fields.

In 1932,Ettore Majorana[30]had shown that a pure state with spin s=N/2 has one to one correspondence with the symmetrized combination of pure states of N-spin 1/2 systems(N-spinors)and provided an elegant geometrical representation of a symmetric multiqubit state as N points on the Bloch sphere.Based on the number of distinct spinors(diversity degree)and the frequency of their occurrence(degeneracy con figuration),a useful classi fication of pure symmetric multiqubit states into SLOCC(stochastic local operations and classical communication)inequivalent families has been achieved.[31,32]Recently,permutation symmetric states have received a revived attention in diverse branches of physics due to their geometrical intuition and experimental importance.[13,14,33,34]

Dicke states|s,m〉,the common eigenstates ofbelonging respectively to eigenvalues s(s+1)¯h2,m¯h,m=-s,-s+1,...,s-1,s,are pure symmetric states consisting of two distinct orthogonal spinors|0〉,|1〉.The different degeneracy con figurations exhaust all Dicke states and each degeneracyconfiguration corresponds to an SLOCC inequivalent class.[31]It is well known that Dicke states exhibit no spinsqueezing inspite of them being entangled states(In fact,spinsqueezing implies pairwise entanglement in multiqubit symmetric states but the converse is not always true).It would therefore be of interest to examine the spin squeezing nature of N qubit symmetric states consisting of all possible permutations of two distinct non-orthogonal spinors,the natural extension of Dicke states.The class of N-qubit pure symmetric states with two distinct spinors (diversity degree 2) are referred to as Dicke-class of states,with the Dicke states correspondingto symmetrized combination of two orthogonal spinors|0〉,|1〉.An analysis of spin squeezing in the Dicke-class of states with two distinct non-orthogonal spinors,taking into account all possible degeneracy con figurations among them,is the aim of this work.In view of the connection between spin squeezing and pairwise entanglement in multiqubit states,[11,13-16]this study will be quite useful in quantum information science.

This paper is organized as follows:The first section gives an introduction to the concept of spin squeezing and provides a brief overview of Majorana representation of pure symmetric multiqubit states.On defining the Dicke-class of states in Section 1,the structure of these states in their canonical form is given in Section 2.The mean spin vector of each SLOCC inequivalent family of Dicke-class of states is identified in Section 2.Among the spin components perpendicular to the mean spin vector,the one which gives minimum varianceis identified in Section 3 for all degeneracy configurations of the Dicke-class of states.Using the results of Section 2 and Section 3,the spin squeezing parameter is explicitly given in Section 4.Illustrative graphs of spin squeezing parameter for several different degeneracy con figurations(corresponding to different SLOCC classes)are given in Section 4,each of them indicating spin squeezing in Dicke-class of states with two distinct non-orthogonal spinors.The amount of spin squeezing in each SLOCC class,as a function of number of qubits is discussed in detail(Section 4).The concluding section(Section 5)summarizes the results of the paper and highlights their significance.

2.Canonical form of Dicke-class of states and identification of their mean spin vector

A pure symmetric state of Nqubits consisting of two spinors,spinor|u1〉appearing k times and spinor|u2〉appearing N-k times,is given in the Majorana representation[30]by

Here P denotes all possible permutations of the two spinors and N is the normalization factor.Without any loss of generality,one can employ a coordinate system in which z-axis is directed along one of the two qubits and x-z plane contains the?other.O?n choosingit readily follows thatbeing real.The canonical form of Dicke-class of states is thus equivalent to the state|Ψk,N-k〉and we have

as the canonical form of Dicke-class of states.One can see that a=0 leads to the spinor|u2〉=|1〉,which is orthogonal to|u1〉=|0〉.The Dicke states are thus given in Majorana representation by

In order to evaluate the spin squeezing parameter for the states|Ψk,N-k〉,one needs to identify the mean spin direction|ˆn0〉and a direction|ˆn⊥〉perpendicular to|ˆn0〉which gives minimum variance ΔˆS⊥of the spin operatorˆS,for all values of N and k＜N.It is worth recalling here that a unit vector along the mean spin direction of any multiqubit symmetric state is given by

In order to find out the mean spin directionwe need to evaluate the expectation values〉and〉.As the spinor|u1〉=|0〉is associated with the unit vector(0,0,1)along z axis andcorresponds to unit vectorin the x-z plane,it is not dif ficult to see that the expectation value〉is zero.On explicit evaluation also,we have veri fied that=0 for all degeneracy con figurations.The expectation values〉are explicitly evaluated for all possible values of k for each N from N=2 to N=5 and are listed in Tables 1 and 2 respectively.

On a careful observation of the expectation values listed in Tables 1,2,a general expression for〈ˆSx〉,〈ˆSy〉applicable for all values of N and k＜N can be obtained,and they are given by

where N is the number of qubits and N is the normalization constant given by

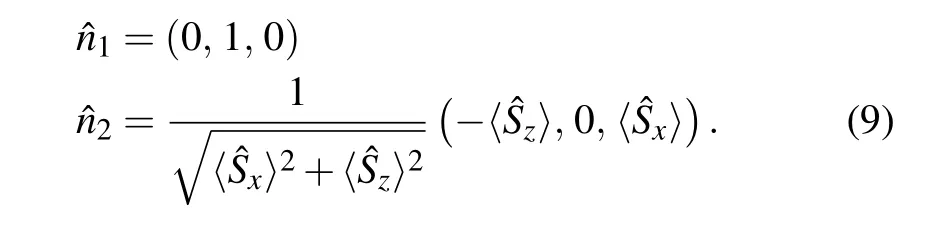
Any vector in the plane de fined by unit vectors,is perpendicular toand the task is to identify a unit vector,for example,,such that the spin componenthas the minimum variance.

Table 1.〉for different degeneracy con figurations.

Table 1.〉for different degeneracy con figurations.

images/BZ_88_268_2444_1143_3154.png

Table 2.〉for different degeneracy con figurations.

Table 2.〉for different degeneracy con figurations.

N=2,k=1 [1/(1+a2)][2a2]N=3,k=2 [1/2(1+2a2)][1+8a2]N=3,k=1 [1/2(1+2a2)][4a4+6a2-1]N=4,k=3 [1/(1+3a2)][1+7a2]N=4,k=2 [1/(1+4a2+a4)][6a4+6a2]N=4,k=1 [1/(1+3a2)][6a4+3a2-1]N=5,k=4 [1/2(1+4a2)][3+22a2]N=5,k=3 [1/2(1+6a2+3a4)][1+22a2+27a4]N=5,k=2 [1/2(1+6a2+3a4)][6a6+30a2+45a4+1]N=5,k=1 [1/2(1+4a2)][4a2+24a4-3]

3.Identi fication ofthe minimum variance))mmiinnn

We recall here the definition of spin squeezing adopted in Ref.[4].A pure symmetric state of N qubits is said to be squeezed in a direction perpendicular to the mean spin direction,iff the spin squeezing parameter ξ given by

lies between 0 and 1(0≤ξ＜1).

A straight forward calculation gives leading to

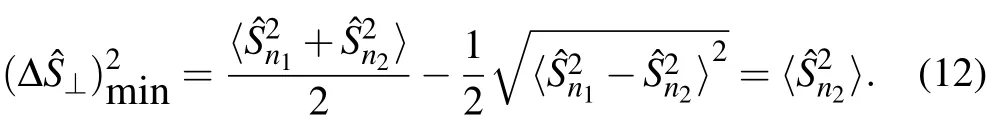
Equation(12)provides an expression for the minimum variance ofthe spin component perpendicularto the mean spin direction.The relationalso identi fiesas,the direction along which the component of the spin has minimum variance.

Table 3 lists the expressions for〉for all degeneracy con figurations possible for N=2 to N=5.

Table 3.〉for different degeneracy con figurations.

Table 3.〉for different degeneracy con figurations.

images/BZ_89_496_1014_2013_1076.png22(1+a2)132 N=3,k=2 34+ 1(1+2a2)■12M21+2M1M2a+M1M3+M22■N=3,k=1 34+ 1(1+2a2)■12M23+2M3M2a+M1M3+M22■N=4,k=2 1+[M21+4M1M2a+M22a2+2M1M3(1+a2)+2M22(1+a2)+4M2M3a+(1/2)M23]2(1+4a2+a4)N=4,k=1 1+ 3(1+3a2)■12M1M3+12M22+2M2M3a+12M23(1+a2)■N=5,k=4 54+ 4(1+4a2)■12M1M3+12M22+3M2M1a+34M21(1+2a2)■N=5,k=3 54+(3/2)M21(1+2a2)+6M1M2(2+a2)a+3M22a2+3M1M3(1+2a2)+3M22(1+2a2)+6M2M3a+(1/2)M2(1+6a2+3a4)3 N=5,k=2 5(1+6a2+3a4)N=5,k=1 5 4+[(1/2)M21+6M1M2a+3M22a2+3M1M3(1+2a2)+3M22(1+2a2)+6M2M3a(2+a2)+(3/2)M23(1+2a2)]+ 4images/BZ_89_496_1770_2013_1815.png■1MM+1M2+3MMa+3M2(1+2a2)■

In Table 3,

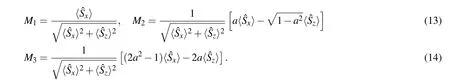
By careful analysis one can obtain a general expression for〈ˆS2n2〉for N qubits as

The spin squeezing parameter(See Eq.(10))now turns out to be

and can be readily evaluated for all values of N and k＜N.The variation of ξ with respect to the real parameter a(0≤ a＜1)is shown in Figs.1-3,for different values of N and k.

Fig.1.Variation of spin-squeezing parameter ξ of the state|Ψk,N-k〉when N=8 and N=12,for different values of k.

Fig.2.Comparitive plots indicating the variation of ξ with respect to k when N=105.Squeezing is seen to be more pronounced when k=52.

One can draw following conclusions about the spin squeezing nature of Dicke-class of states|Ψk,N-k〉.Recall here that spin squeezing is maximum when ξ=0 and there is no spin squeezing when ξ≥ 1.

(i)For any N,the squeezing parameter for the states|Ψk,N-k〉and|ΨN-k,k〉match with each other.This means,interchanging|u1〉with|u2〉in|Ψk,N-k〉(See Eq.(2))does not affect the spin-squeezing property,both of them having the same spin squeezing parameter.

(ii)From Figs.1 and 2,it is evident that for a fixed N,squeezin gincreases(ξ decreases)inthe who lerange 0≤a＜1 with increase in k(k ＜ N).But as,|Ψk,N-k〉and|ΨN-k,k〉have same ξ,we need to consider values of k up to[N/2]where[N/2]=N/2 for even N and[N/2]=(N-1)/2 for odd N.For instance,in Fig.2,the graph for N=105,k=15 is equivalent to the graph for N=105,k=90.Also,when|u1〉,|u2〉are equally distributed,i.e.,when k=[N/2],the squeezing is pronounced in the whole range of parameter a,as can be seen in the graph for N=105,k=52.

(iii)The Dicke states

corresponding to a=0 are seen to be non-squeezed(See Fig.3).In fact,Dicke states with even N and k=N/2 corresponding to equal distribution of|0〉,|1〉,the spin squeezing parameter is unde fined(See Fig.3)as the mean spin direction becomes a null vector.Such Dicke states are the ones with s=N/2 and m=0.For all other Dicke states,with odd or even N,k＜ N,the spin squeezing parameter ξ is greater than 1 as is illustrated explicitly in the graph for N=6,k=1(Fig.3)and indicated in Figs.1 and 2.

Fig.3.Variation of spin-squeezing parameter ξ of the state|Ψ1,5〉and|Ψ3,3〉corresponding to N=6,k=1,N=6,k=3 respectively.

One can readily conclude that Dicke-class of states|Ψk,N-k〉,containing two distinct non-orthogonal spinors(with a/=0)exhibit squeezing,the amount of squeezing varying with the degeneracy con figuration{k,N-k}.

4.Conclusion

Using the Majorana representation of pure symmetric multiqubit states with two distinct spinors,we have studied their spin squeezing properties.By explicit determination of the mean spin vector and minimum variance of the states under consideration,the Kitegawa-Ueda spin squeezing parameter[4]is determined.Through illustrative graphs of the variation of the spin squeezing parameter,it is shown that symmetric multiqubit states characterized by two distinct nonorthogonal spinors exhibit spin-squeezing.For a fixed number of qubits in the state,the squeezing is seen to be maximum if the two distinct spinors characterizing the state are equal in number.Due to the usefulness of spin squeezed states in high precision,low noise spectroscopy and in quantum information theory,the study presented here is of importance.We wish to mention here that spin squeezing parameter of the Dickeclass of states considered here are determined in an alternative manner in Ref.[35]using the two-qubit density matrices of the symmetric multiqubit state,the results matching with that presented here.The study of spin squeezing for the pure symmetric multiqubit states having diversity degree 3 is under progress.

Acknowledgements

One of the authors(K S Akhilesh)thanks the University Grant Commission for providing BSR-RFSMS fellowship during this work.We thank Dr.A R Usha Devi for insightful discussions.