超声光栅测量透镜焦距
王 平, 刘竹琴
(延安大学 物理与电子信息学院, 陕西 延安 716000)
透镜焦距是表征其成像性质的重要参数,实验室中常用的几种测量透镜焦距的方法均为根据物像关系设计的,有物距像距法、位移法、自准直法[1-5]等方法。为了进一步拓宽透镜焦距测量的方法,以及让学生了解超声光栅在测量中的应用,利用超声衍射现象对透镜的焦距进行测量。
1 实验原理
1.1 实验装置及仪器
本实验仪器由控制主机、低压钠灯、光学导轨、光学狭缝、准直透镜、超声池、测微目镜、高频连接线以及待测透镜组成,实验装置如图1所示。

图1 实验装置图
1.2 实验原理
1.2.1 超声光栅的原理
压电陶瓷片(PZT)在高频信号源(频率约10 MHz)的交变电场的感应下,产生周期性伸缩振动而形成超声波,使液体分子发生周期性的变化,导致液体的折射率也相应地发生周期性的变化,构成疏密波[6]。当平行单色光垂直于超声波传播方向通过这疏密相同的液体时,就会发生衍射,这一效果类似光栅,所以称为超声光栅。
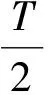
在某个时刻t,相邻两个密集区域的距离λ即为液体中传播的行波的波长,当平行光通过超声光栅时,光线衍射的主极大位置由以下光栅方程[9]决定:
Λsinφk=kλ(k=0,1,2,…)
(1)
式中,Λ为超声波长,k为衍射条纹级次,λ为入射光波长。
1.2.2 凸透镜焦距的测量
测量光路图如图2所示,S为单色光源,L1为准直透镜,PZT为压电陶瓷片,L2为待测透镜,f凸为待测凸透镜的焦距,lk为衍射零级光谱线至第k级光谱线的距离。

图2 超声光栅测量凸透镜焦距光路图
由于φ角很小,sinφk≈lk/f凸。
因此有
Λ=kλ/sinφk=kλf凸/lk
(2)
设超声波在液体中的传播速度为v,则有
v=Λν=kλf凸ν/lk
(3)
式中ν为超声波的频率。
凸透镜的焦距为

(4)
式中,Δk为级次差,Δlk为Δlk对应条纹间距。
1.2.3 凹透镜焦距的测量
取一个焦距f已知的凸透镜和待测的凹透镜共轴组成光具组,调节光具组与测微目镜的位置,测量光具组两透镜之间的距离d。由上述测量原理可得光具组的焦距f合为

(5)
由文献[10]可知光具组的焦距为

(6)
式中,f为已知凸透镜的焦距,f凹为待测的凹透镜焦距,d为两个透镜之间的间隔。
待测凹透镜的焦距为

(7)
2 实验方法
(1) 将器件按图3放置,将超声波光栅实验仪与低压钠灯和超声池进行连接,将各光学元件调节至共轴等高,调整目镜的焦距,使得视野中的十字丝清晰,打开电源,使钠光匀称的照射在狭缝上。
(2) 将蒸馏水倒入超声池中,将超声池固定在支架上,扭转超声池的位置,使得它的两侧大致垂直于主光轴。
(3) 调整导轨上测微目镜以及待测透镜的位置,直到在目镜中可以看到清晰的衍射条纹为止。
(4) 调整准直透镜的位置,直到条纹之间的距离不变。
(5) 轻微转动液槽,直到从目镜中观察到清晰的衍射条纹为止。
(6) 为了防止回程误差,测量时单向读数。
3 测量结果
3.1 凸透镜焦距
超声波的频率υ=10.025 MHz,水中声速v=1 497 m/s用逐差法处理数据求出各谱线衍射条纹的平均间距,数据见表1。
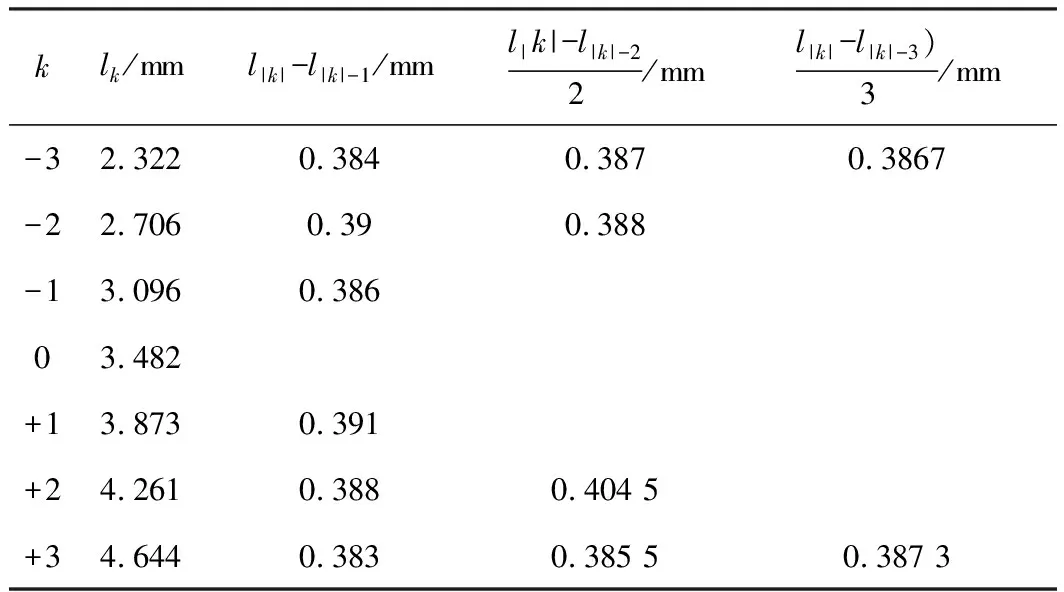
表1 逐差法处理数据的计算表
衍射条纹的平均间距为
(l|k|-l|k|-3)/3]=0.388 4mm
凸透镜的焦距为
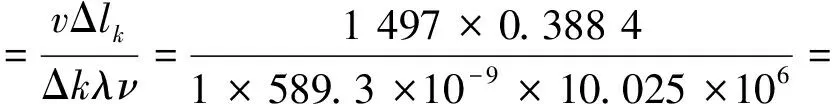
98.42 mm
根据参考文献[11-12]得Δlk的A类不确定度为uA(Δlk)=0.002 mm。
实验所用的测微目镜的误差限为Δ=0.01 mm,则Δlk的B类不确定度为uB(Δlk)=0.006 mm。
则Δlk的合成不确定度为uc(Δlk)=0.006 mm。
由误差传递公式得:u(f凸)=1.5 mm。
因此,得到透镜的焦距为f凸=(98.4±1.5)mm
与待测凸透镜的标准值100.000 mm进行比较,相对误差为1.6%。
3.2 凹透镜焦距
超声波的频率为10.025 MHz,用逐差法处理数据求出各谱线衍射条纹的平均间距,数据计算见表2。

表2 逐差法处理数据的计算表
衍射条纹的平均间距为
(l|k|-l|k|-3)/3]=1.074 1mm
待测凹透镜的焦距为
f凹=60.46 mm
uA(Δlk)=0.001 mm
uB(Δlk)=0.006 mm
uc(Δlk)=0.006 mm
由误差传递公式得:
u(f凹)=0.8 mm
测量结果为f凹=(-60.5±0.8)mm
与待测凹透镜的标准值60.000 mm进行比较,相对误差为0.83%。
4 结语
本文设计了利用超声光栅测量透镜焦距的方案,测量了待测透镜的焦距,并与标准值进行了比较,得出实验误差分别为1.6%和0.83%,实验结果较为理想,保证了测量结果的可靠性。用超声光栅测量透镜的焦距,原理简单,方法可靠,为透镜焦距的测量提供了一种新的方法。通过本次实验,激发了学生对物理实验的学习兴趣,能培养学生的实验操作能力、观察能力、和思考问题、创新意识以及解决问题的能力。

