适应性回归分析(Ⅲ)构建具有混合结构的回归模型——

罗艳虹，胡良平

(1.山西医科大学公共卫生学院卫生统计学教研室，山西 太原 030001；2.世界中医药学会联合会临床科研统计学专业委员会，北京 100029；3.军事科学院研究生院，北京 100850

1 基于多个回归模型采用ADAPTIVEREG过程实现一次性拟合

1.1 问题与模型

【实例1】假定在自变量的定义域内，可以构造出三个回归模型，它们分别为指数回归模型、对数回归模型和直线回归模型[1-2]。这三个回归模型的表达式见式(1)。

(1)

是否可以通过一个SAS过程步来一次性拟合出上述三个回归模型？

1.2 利用ADAPTIVEREG过程实现上述要求

1.2.1 所需要的SAS程序

data Mixture;

drop i;

do i=1 to 1000;

X=ranuni(1);

C=int(3*ranuni(1));

if C=0 then Y=exp(5*(X-0.3)**2)+rannor(1);

else if C=1 then Y=log(X*(1-X))+rannor(1);

else Y=7*X+rannor(1);

output;

end;

run;

ods graphics on;

proc adaptivereg data=Mixture plots=fit;

class c;

model y=c x;

run;

1.2.2 SAS数据步程序说明

在SAS数据步程序中，拟产生1 000个观测(即样本含量N=1 000)；将自变量X设置为在“0～1”区间上变化且服从均匀分布的随机变量；首先将分类变量C设置为在“0～1”区间上变化且服从均匀分布的随机变量，然后将变量C乘以3，最后再将其取整(这样做的目的是使“C”成为随机变量，而不是一般变量，也就是说，它在数据集中的取值仍为0～2，但不是按确定性的顺序出现的，而是随机出现的)；接下来按式(1)进行计算，得出C在取不同值条件下的因变量y的数值。应注意：在因变量y的每个数值上，还加上了一个服从N(0,1)分布的随机变量的数值，其意义在于：因变量y也是一个随机变量，而不是一个一般变量。

1.2.3 SAS过程步程序说明

调用“ADAPTIVEREG过程”，在过程步语句中，要求绘制图形；使用“CLASS语句”，指定分类变量为“C”；在“MODEL语句”中，包含了两个自变量，一个为变量C、另一个为变量X。

1.2.4 SAS主要输出结果及解释

拟合统计量GCV1.08046GCV R-Square0.90279Effective Degrees of Freedom25R-Square0.90740Adjusted R-Square0.90628Mean Square Error1.04064Average Square Error1.02711

以上为拟合统计量的计算结果，R2和调整R2分别为0.90740和0.90628，说明模型对资料的拟合效果比较好。

向后选择后的回归样条模型名称系数父级变量结点水平Basis05.3829InterceptBasis1-4.3871Basis0C10Basis332.7761Basis0C1Basis520.2859Basis4X0.7665Basis7-11.4183Basis2X0.7665Basis8-7.0758Basis2X0.7665Basis958.4911Basis3X0.5531Basis10-71.6388Basis3X0.5531Basis11-69.0764Basis3X0.04580Basis13-119.71Basis3X0.9526Basis1566.5733Basis1X0.9499Basis176.6681Basis1X0.5143Basis19-185.21Basis1X0.9890

以上为“向后选择后的回归样条模型”中“各基函数”及其回归系数，以“基函数”为新“自变量”的适应性回归模型比式(1)更复杂。

ANOVA分解功能性成分基数DF变化量(若忽略)失拟GCVC241112.501.1519C X10203773.943.7690

以上为“方差分析分解”的计算结果，对因变量y影响较大的是“C”与“X”之间的交互作用项，其次是变量C。

变量重要性 变量基数重要性C12100.00X1050.68

以上为两个变量“C”与“X”对因变量y的重要性的计算结果，可以看出：变量C对因变量y的影响最大，其次是变量X。

拟合结果用图示法呈现，见图1。

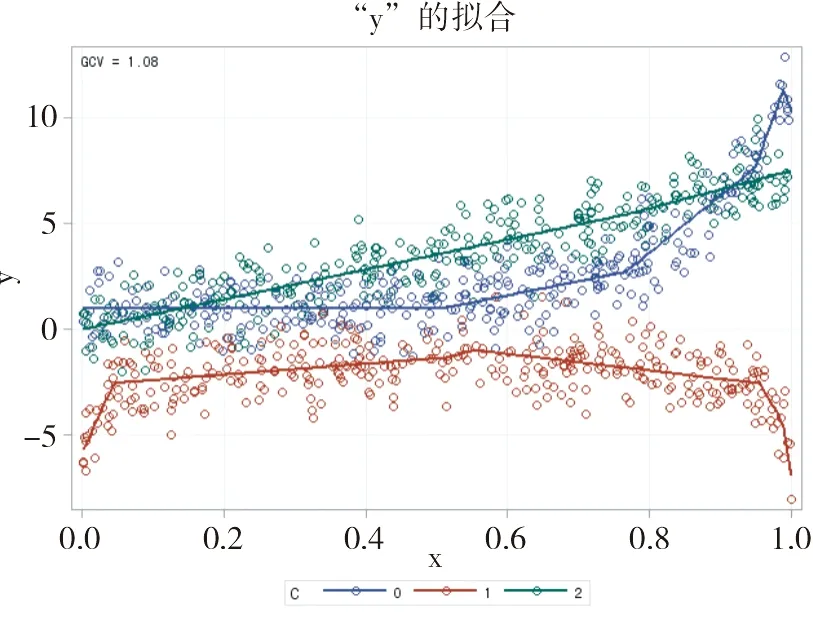
图1 ADAPTIVEREG过程按式(1)拟合的结果

由图1可知：自上而下有三条线，第1条为“直线”，对应式(1)中第3式；第2条为“指数曲线”，对应式(1)中第1式；第3条为“对数曲线”，对应式(1)中第2式。

2 基于具有混合结构的数据集采用ADAPTIVEREG过程实现一次性拟合

2.1 问题与数据结构

【实例2】假定有一个具有混合结构的数据集。见表1。

在此次研究中,观察组患者的腹胀几率是5.46%,对照组的腹胀几率是21.82%,两组结果对比存在统计学差异性(P<0.05)。观察组患者的胃肠蠕动时间、肠鸣音、肛门排气时间等均比对照组短,两组结果存在统计学差异性(P<0.05)。观察组临床护理满意度是94.54%,对照组是76.37%,结果存在统计学差异性(P<0.05)。

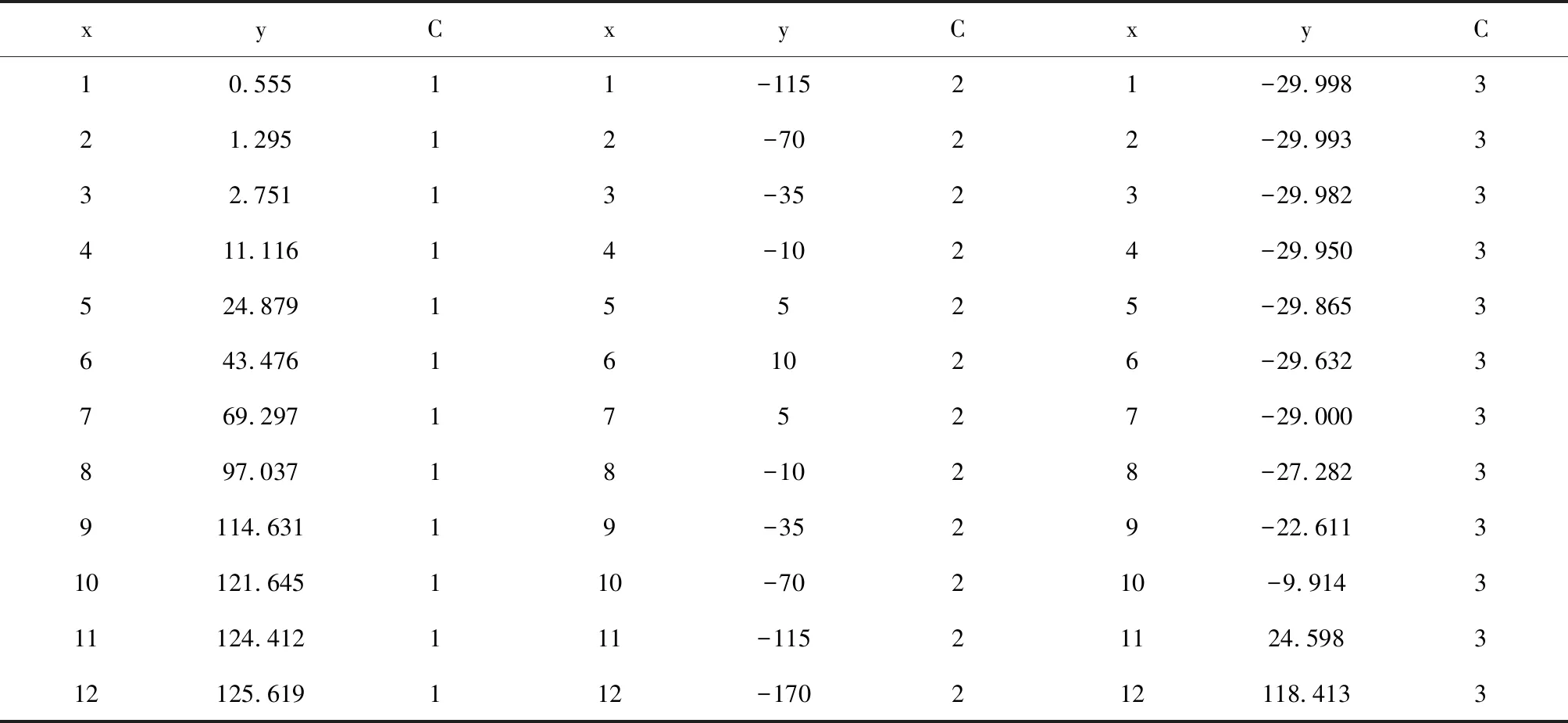
表1 一个具有三类(C=1、2、3)结构不同的混合型数据集

注：在C=1、2、3类的数据集中，x的取值均为1～12，但y的取值是不同的

【问题】试在每一类中，构建y依赖x变化而变化的回归模型。

2.2 试采用ADAPTIVEREG过程直接拟合该数据集

2.2.1 创建SAS数据集

所需要的SAS数据步程序如下：

Data a1;

INPUT x y c @@;

CARDS;

此处输入表1中12行6列数据;

;

RUN;

所需要的SAS过程步程序如下：

ods graphics on;

proc adaptivereg data=a1 plots=fit;

class c;

model y=c x;

run;

2.2.3 显示SAS主要分析结果

拟合统计量GCV132.61471GCV R-Square0.97285Effective Degrees of Freedom21 R-Square0.99501 Adjusted R-Square0.99302 Mean Square Error33.15368 Average Square Error23.02339

以上为“拟合统计量”的计算结果。由R2和调整R2的计算结果可知，模型对资料的拟合效果比较好。

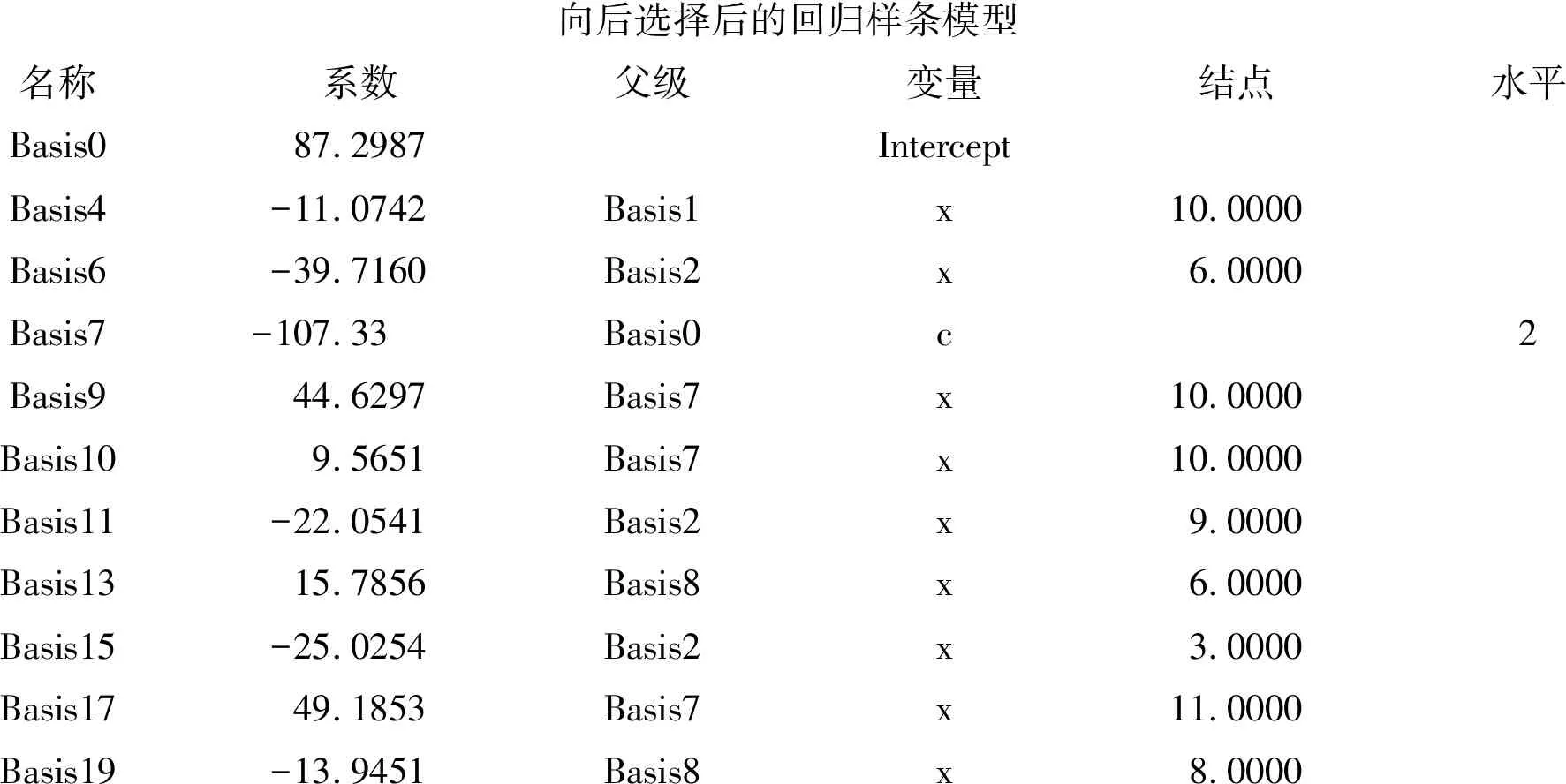
向后选择后的回归样条模型名称系数父级变量结点水平Basis087.2987InterceptBasis4-11.0742Basis1x10.0000Basis6-39.7160Basis2x6.0000Basis7-107.33Basis0c2Basis944.6297Basis7x10.0000Basis109.5651Basis7x10.0000Basis11-22.0541Basis2x9.0000Basis1315.7856Basis8x6.0000Basis15-25.0254Basis2x3.0000Basis1749.1853Basis7x11.0000Basis19-13.9451Basis8x8.0000

以上为“向后选择后的回归样条模型”的计算结果，需要用到19个“基函数”。

ANOVA分解功能性成分基数DF变化量(若忽略)失拟GCVC12128071565.97C X9181633895296.08

以上为“方差分析分解”的计算结果，说明变量C和“C”与“X”的交互作用项对因变量y的影响很大。

变量重要性变量基数重要性C9100.00X1093.90

以上是对两个变量的重要性所做的评价，两个变量对于因变量y的影响都很大。

由于模型的表达式非常复杂且不直观，SAS采用图形方式呈现模型拟合结果。见图2。

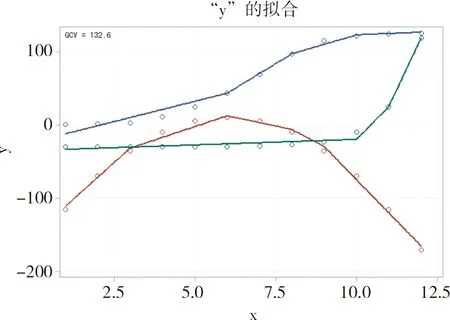
图2 采用ADAPTIVEREG过程拟合表1资料的结果以图形呈现

在图2中，可以比较清楚地看出：在“C=1”类中，y与x之间呈现“Logistic曲线”关系；在“C=2”类中，y与x之间呈现“抛物线”关系；在“C=3”类中，y与x之间呈现“指数曲线”关系。

2.3 数据结构的揭秘

在表1的“C=1”类中，(x，y)的两列数据来自文献[3]，该资料描述的是“某县疟疾发病的季节性特点”，即某县1961年-1996年疟疾的月累计发病率(x代表1月-12月，y代表“累计发病率”，单位为“1/10万”)。绘制该资料的散布图，呈现“Logistic曲线”变化趋势，适合拟合“Logistic曲线回归模型”。

在表1的“C=2”类中，(x，y)的两列数据中的“x”保持不变，而“y”列数据是采用如下的式(2)计算出来的：

y=-5×(x-6)2+10

(2)

式(2)表达的是一个y关于x 的“二次抛物线模型”。

在表1的“C=3”类中，(x，y)的两列数据中的“x”保持不变，而“y”列数据是采用如下的式(3)计算出来的：

y=e(x-7)-30

(3)

式(3)表达的是一个y关于x 的“指数曲线模型”。

结合上面图1中呈现的“三条曲线”及其解释，不难发现：适应性回归样条算法给出的结果与数据所代表的真实模型是基本吻合的。

3 讨论与结论

3.1 讨论

“实例1”与“实例2”看起来有所不同，前者似乎是从“模型”出发，产生“数据”，再用“ADAPTIVEREG过程”去拟合数据；而后者似乎是从“数据”出发，采用“ADAPTIVEREG过程”去拟合数据，再交代各类数据所代表的“模型”。其实，二者在本质上是完全一样的。对于“ADAPTIVEREG过程”而言，它并不知晓正在拟合的“数据”究竟包含了“哪几种模型”或存在“哪些客观规律”，只是基于“特定类中两变量之间的数量关系”并依据“适应性回归样条算法”去逐一构造“基函数”，在“失拟(LOF)”和“广义交叉验证(GCV)”等的“拟合优度评价指标”的“监控”之下，找到“基函数”及其组合。

3.2 结论

适应性回归样条算法(由ADAPTIVEREG过程实现)确实具有一定的揭示“混杂结构数据集”中隐藏的数据规律的“能力”；然而，它给出的基于“基函数”的“回归模型”过于复杂且很不直观；通过“图形方式”呈现的结果虽然很直观，但很不“精确”，不同的分析者可能会给出不同的“解读结果”。但是，图形呈现的结果确实可以给分析者提供一些有价值的“分析线索”或“积极暗示”，有利于分析者缩小“探索性研究的空间”[4]。