试论抽丝剥茧精细剖析乘法分配律

郑春梅

摘 要：数学教学中教师要引导学生熟练掌握规律性的知识点，文章从乘法分配律的教学入手，从借用图形理解规律、分门别类深入研究分配律两个方面阐述乘法分配律的学习技巧。

关键词：数学教学;乘法分配律;数学思维能力;图形

中图分类号：G623.5 文献标志码：A 文章编号：1008-3561（2019）13-0085-01

乘法分配律是四年级下册数学教学内容，在后续的五、六年级也有涉及，它是运算律中很重要的规则，其应用也十分广泛。目前在教学中，部分学生对乘法分配律的掌握还不十分理想，在计算题目时常常出错，针对这一情况，笔者运用逐层递进的教学方法，将乘法分配律抽丝剥茧，以提高学生的理解和掌握程度。

一、借用图形理解规律

在教学乘法分配律时，教师可以结合图形排列阵型，让学生在数图形数目的过程中，自然认知乘法分配律。如图1的图形矩阵就能很好地诠释分配律的运用。计算图标总数时，要根据行数与列数的连续性和分离性，提取相同因数，通过计数揭示分配律的建模原理。

点算“笑脸”数目的方法。方法一：（5+3）×4=8×4=32（个）。方法二：5×4+3×4=20+12=32（个）。很显然，根据计算结果，可以推定（5+3）×4=5×4+3×4。另外也可以打通两种方法的壁垒，（5+3）×4是将每行（包括白脸和黑脸）看作8个，共有4行，而算式5×4+3×4，则是将白脸和黑脸一分为二，先分别算出白脸和黑脸的数目，再来合并。这些点算过程学生可以自行体驗揣摩，有了直观形象作基础，对于乘法分配律的理解、推导、运用，就会畅行无阻。

二、分门别类，深入研究分配律

要弄清楚乘法分配律，就要将分配律所有的原形变式一一呈现，让学生把乘法分配律的所有形式融会贯通，这样在运用时就会得心应手。在教学中，教师不妨将分配律细化分类，姑且分为顺分配律和逆分配律两大类。因数依次逐项乘以各加数、减数的，最后合并同类项求和或差的是“顺分配律”;先求出各个加数、减数的和或差，然后与共用因数相乘求积的，称为“逆分配律”。

1.顺分配律

（1）一般模式：（a±b）×c=a×c±b×c。这是一般模式，因为有了前面的积淀，学生很容易弄明白先求出和差再扩大倍数，可以反过来先求出括号里每项的倍数，再求和差。（2）拆项模式：c×x=c×（a±b）。如：76×102=76×（100+2）=76×100+76×2=7600+ 152=7752。这种形式有隐蔽性，难度较大，学生不容易观察，教师可以置于生活情境中促进学生理解。如：学校有102人订购校服，每套校服76元，全校共收校服费用多少钱？让同学们互相交流讨论，看看怎么计算才能又快又准。学生经过小组合作探究，发现这样算比较简便：先将102人分为两组，一组为100人，另一组为2人，第一组缴费总额为76×100=7600（元），第二组缴费总额为76×2=152（元），整体缴费总计为7600+152=7752（元），用算式表示就是76×102=76×（100+2）= 76×100+76×2=7600+ 152=7752（元）。通过分析具体情境，学生知道“拆”数可以降低计算难度。

2.逆分配律

严格说，乘法分配律应该是（a±b）×c=a×c±b×c这种形式，这在初中代数里面有所交代。习惯上把a×c±b×c=（a±b）×c也称为乘法分配律，小学生只需要知道它们是可逆变化就行。

（1）一般模式：a×c±b×c=（a±b）×c。在教学过程中，教师可以把a×c±b×c=（a±b）×c这种模式命名为“逆分配律”。对于a×c±b×c=（a±b）×c这种形式，可以提取共用乘数，先求和差再求倍数，也可以通过几何图形面积来赋予现实意义。

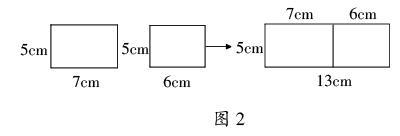
图2中，左面的两个图形的总面积是：5×7+5×6=35+30= 65（cm2）。右图的面积是：（7+6）×5=65（cm2）。通过图形的组合可以看出：5×7+5×6=（7+6）×5。通过上述探究，学生比较轻松地弄明白了这种“逆分配律”的普通模式。

（2）分离因数“1”：a×c±c=（a±1）×c。这是“逆分配律”中的另一种特殊形式，出错率较高。因为它在形式上好像差了一个相异的因数，相同共用因数似乎缺项，直观上看不出有可以提取公因数的条件。因此学生就会有困惑。此时，教师就需要提示c=c×1，引导学生推出a×c±c=a×c±c×1=（a±1）×c，当然仍可借用生活中的特殊情境揭示这一规律。

综上所述，学生掌握方法，就会对乘法分配律的认识更上一层楼，运用时就可以减少误判，这是经过长期教学实践总结出的宝贵经验。学生娴熟运用这些方法，就会对乘法分配律的特性和适用情形有清晰的认识，从而提高解题效率。

参考文献：

[1]卢杰夫.多层次感悟乘法分配律的内在逻辑——“乘法分配律”教学片断与思考[J].小学数学教育，2018（22）.

[2]胡红美.慢思，知其然;慢渗，知其所以然——《乘法分配律》教学实践与反思[J].数学教学通讯，2018（28）.