基于Kalman滤波数据融合方法的超声波气体泄漏定位研究

(北京理工大学自动化学院， 北京 100081)

引言

现代工业和生活中广泛使用了用于存储和输送压缩气体的压力容器以及管道等， 气密性是这些设备质量和安全的重要指标之一，因此气体泄漏检测非常重要[1-2]。一些传统的泄漏检测方法，比如压差法、绝对压力法等，操作非常复杂并且对技术人员要求较高，而且一般不具有实时性[3]。现代工业中广泛利用泄漏产生超声波的原理来进行泄漏检测， 通过分析高压气体从密封容器或者管道的泄漏孔喷射产生的超声波，达到泄漏检测与泄漏点定位的目的[4]。国内外学者根据不同研究重点开发了多种超声波气体泄漏检测仪， 采用的检测定位算法主要包括以时延技术为基础的到达时间差定位算法(TDOA)和以信号传播特性为基础的能量衰减算法(ED)。然而到达时间差定位算法误差不稳定：当传感器与泄漏点距离较大时，能量衰减定位算法所得的声压比值接近1，这使得该方法对误差非常敏感，故采用基于扩展Kalman滤波的数据融合方法，利用传感器阵列，将TDOA定位法和ED定位法的计算结果进行联合计算出泄漏点与阵列中各换能器之间的距离，最终通过几何方法计算出泄漏点与传感器平面的垂直距离和相应的投影坐标。通过实验证明了该算法的有效性及其与传统算法相比的优越性。

1 气体泄漏模型

对于各种液压、气压密闭容器，管道或是焊接加工接口等由于加工质量不过关、安装不合理，或者是长期连续使用等原因都会导致细微的孔隙和裂缝产生，因此在压力系统的作用下就会产生流体泄漏[5]。当孔隙的尺寸足够小，而容器的内外压力差足够大的时候，从孔隙中泄漏产生的气体的流速会很大，而且泄漏的气体的雷诺数通常比较高，因此就产生了湍流射流。对于湍流射流来说，从靠近狭缝处的初始段至主段以后很长的区域内将会不断地产生旋涡，而这些漩涡又在不断地发展破裂产生新的漩涡，气体泄漏模型如图1所示。关于这些漩涡，1952年Lighthill就给出了论述[6]，即漩涡产生的涡流实际上就是流体的声音。

图1 气体泄漏模型

实际工程中，容器或管道的泄漏孔很小，其孔径大多在0.1 mm量级，甚至更小。超声波的产生区域在喷口以外5倍孔径的区域，即该区域长度在1 mm量级。通常的泄漏检测中，传感器与泄漏孔的距离在100 mm量级上，远大于超声波的产生区域，故可以将喷注噪声产生区域看做是点声源，声波以球面向外传播。泄漏产生的声波的频率谱范围一般是从十几千赫兹到接近百千赫兹，但是能量大都会集中在10～50 kHz内，属于超声波频谱范围之内，因此利用超声波传感器阵列对其进行采集、处理，可以估计出点声源的位置，即泄漏点的位置。

2 到达时间差定位算法

到达时间定位方法的原理是测量信号从信号源到达观测点的时间，进而得到信号源与观测点之间的距离，多观测点的信息联合解算出信号源位置。TDOA定位法可以消除对时间基准的依赖性，因而可以降低成本并仍然保证一定的定位精度，但是需要有较好的时延估计方法，才能保证较高的时延估计精度[7-8]。

图2为泄漏定位算法原理图，假设4个超声波换能器A，B，C，D以正方形平面阵列的形式放置，其坐标为A(x1,y1,z1)，B(x2,y2,z2)，C(x3,y3,z3)，D(x4,y4,z4)，信号到达换能器的时间为t1，t2，t3，t4，信号到达换能器的时间差为Δt12，Δt23，Δt34(下标1对应换能器A，2对应换能器B，以此类推)。

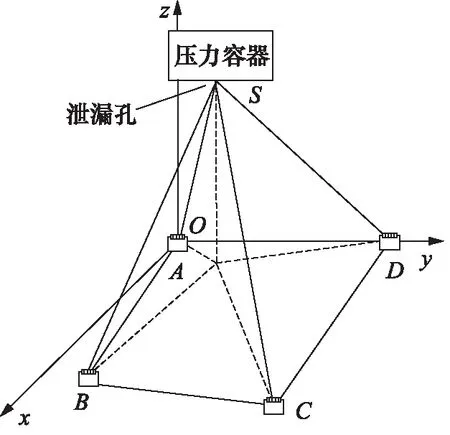
图2 泄漏定位算法原理图

则旋转双曲面方程组如下：

(1)

式中，ξij为到达时间差计算值的误差。方程组为非线性恰定方程组，但是到达时间差误差为随机数，因此上述方程组很难存在解。上述双曲面方程组联合其他数学估计方法，例如最小二乘法或牛顿迭代法等，可以解出方程组的近似解，该解即为泄漏点位置[9]。图3表示泄漏点位于(-10,10,450)、初始迭代值为(10,-10,350)、到达时间差误差在5 μs内时，使用牛顿迭代法计算泄漏点位置的迭代过程。可以看出，迭代过程中系统状态收敛到局部极值，与泄漏点真实位置相差巨大。

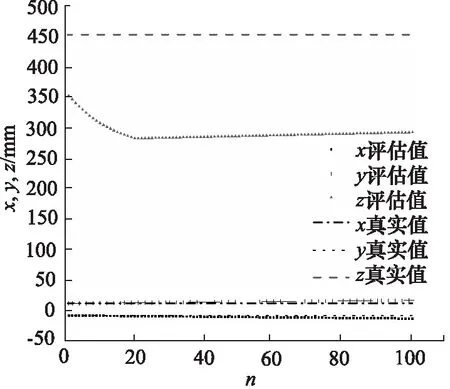
图3 到达时间差算法仿真结果

3 能量衰减定位算法

在使用能量衰减定位算法时，主要利用的是信号的能量在传播过程中随传播距离的增大而逐渐衰减的原理，导致不同换能器接收到的来自同一泄漏声源的超声波信号在强度上的不同，从而构成约束条件，与泄漏点和超声波换能器阵列构成的几何位置关系，联立方程组得出泄漏孔所在的位置坐标。能量衰减定位方法因为硬件简单、低成本等特点，在无线传感器网络领域的节点定位中使用较多[10-11]。

超声波可被视为球面波，将声波的衰减模型描述为：

(2)

式中，pi(t)为t时刻换能器i处声压值；p(t)为t时刻声源的声压值；rs与ri分别为声源与换能器的位置向量；npi(t)为声压噪声，可以用高斯分布近似。

本研究选择的压电式超声波换能器对声压敏感，换能器的输出值正比于声波的声压，即：

ui(t)=gipi(t)

(3)

式中，gi为换能器i的接收系数。

考虑不存在噪声的情况下，换能器i,j处声压比值kij为：

(4)

则实际检测时，由平面阵中传感器测得信号得到的定位方程组为:

(5)

简单地说，到达时间差定位算法是根据泄漏点与任两传感器距离的差值做出以传感器位置为焦点、距离差为长轴的空间旋转双曲面，多个双曲面的交点即是泄漏点位置。能量衰减算法是根据泄漏点与任两传感器距离的比值得出一球面，多个球面的交点为泄漏点位置，如图4所示。

图4 面型传感器阵列定位示意图

4 基于Kalman滤波的融合定位算法

数据融合就是将多传感器测得信息或者多种算法得到的最终或中间结果联合来提高最终结果或估计的精确度的方法[12-13]。

数据融合可分为3个层次，数据层融合、特征层融合与决策层融合。数据层融合是将多传感器测得的最底层数据送至数据融合中心进行处理，得到需要的结果，计算量大时效性差；特征层融合是先抽象出多传感器或者多算法的特征向量，将各特征向量送至融合中心进行关联，根据融合结果做出判断决策；决策层融合是先利用各传感器或算法分别计算出结果，再将结果融合得到最终值，精度较低。

本研究是两种算法的融合，无法进行数据层融合。决策层融合相当于根据两种算法分别求出泄漏点位置，再对各自的估计结果进行融合。由于单独的到达时间差算法与能量衰减算法估计结果误差大，不适合决策层融合。本研究中，到达时间差算法(TDOA)得到泄漏点与传感器的距离差,能量衰减算法(ED)得到泄漏点与传感器的距离比值。特征层融合是根据距离差与距离比值送到融合处理中心进行融合计算，本研究采用特征层融合。

数据融合常用方法包括概率论方法、D-S证据理论、神经网络与Kalman滤波等，本研究采用Kalman滤波方法，该方法适用于实时处理动态环境中的信息。Kalman滤波属于递归滤波器，通常被用于动态系统中估计含有噪声的系统状态值。然而Kalman滤波理论只能应用于线性系统，本研究的测量方程涉及泄漏点到传感器的距离比值，含有非线性成分，所以本研究采用扩展Kalman滤波方法(EKF)进行数据融合。

本研究采用的数据融合的结构框图如图5所示。将到达时间差算法与能量衰减算法视为两子系统，分别得到到达时间差与声压比值。图5中特征抽取表示将到达时间差与声压比值转换为到达距离差与到达距离比，关联即将到达距离差与到达距离比联合作为数据融合的观测值。数据融合部分采用扩展Kalman滤波理论进行泄漏点位置的迭代计算，最终得到位置估计结果。

图5 数据融合结构框图

关于数据融合部分的模型，本研究将超声波泄漏检测类比为一个控制系统，假设泄漏点位置坐标x，y，z为系统状态，r=[x,y,z]T为状态向量，根据不同传感器测得的时间差和声压比计算距离差Δsij与距离比值δsij，作为系统的特征值，将数据融合看作对系统状态的估计。

首先，建立系统的状态转移方程与观测方程。本研究考虑泄漏检测时泄漏点相对于传感器阵列静止的情况，则该离散控制过程的状态方程可以描述为:

r(k+1)=Φr(k)+ω(k)

(6)

式中，本研究中泄漏点坐标的单位为mm。Φ为状态转移矩阵，Φ=I3为单位阵。ω(k)∈R3为过程噪声，可以将其元素当做均值为0的高斯白噪声。可以将到达时间差算法与能量衰减算法看做系统的两子系统，前者的特征向量为泄漏点到传感器的距离差值Δs，后者的特征向量为距离比值δs。本研究采用特征层的数据融合，即将两子系统的特征向量关联，则将系统的观测方程表示为：

y(k)=h(r(k))+υ(k)

(7)

式中，y(k)=[Δs12(k), Δs23(k), Δs34(k),δs12(k),δs23(k),δs34(k)]T为系统的观测向量； Δsij=c·Δtij，δsij=kij，v(k)∈R6表示观测噪声，其元素可用均值为0的高斯白噪声近似。其中，h(r(k))为系统的非线性观测函数:

(8)

其中，si(k) (i=1,2,3,4)表示泄漏点与传感器i之间的距离：

(9)

过程噪声主要由检测过程中传感器阵列与泄漏点的相对移动造成，观测噪声由信号调理采集环节以及计算过程引入，故认为过程噪声与观测噪声没有相关性。

根据扩展Kalman滤波理论，系统的先验状态估计为:

(10)

P(k+1|k)=ΦP(k|k)ΦT+Q

(11)

由k+1时刻的观测值，得到k+1时刻实际观测值与先验估计的观测值间的差，也称为新息：

(12)

系统的后验估计为:

(13)

其中，K(k+1)代表kalman系数，也称为kalman增益，为:

K(k+1)=P(k+1|k)HT(k+1)

[H(k+1)P(k+1|k)HT(k+1)+R]-1(14)

H(k+1)表示根据k+1时刻先验状态估计局部线性化得到的观测矩阵，为h(r(k))的雅克比矩阵。后验状态估计的误差协方差矩阵为:

P(k+1|k+1)=[I3-K(k+1)H(k+1)]

P(k+1|k)

(15)

给定迭代的初始状态估计及其误差协方差为:

P(0|0)=P0

(16)

根据以上的滤波模型进行扩展Kalman滤波的迭代，直至相邻两次系统状态向量差的模的平方小于某一固定值时，输出融合结果。

5 实验证明

为验证本研究提出的泄漏定位算法的性能，建立了一套由4个传感器组成的面阵、检测机箱、显示器和存在0.1 mm直径小孔的尼龙罐构成的实验装置，实验装置如图6所示，检测机箱内包含前置调理电路、数据采集卡、单板电脑、电源和风扇。传感器采集的信号经过前置调理电路的放大和滤波、数据采集卡的数模转换后，输入单板电脑进行定位计算，最终的定位结果显示在显示屏中，使用的软件平台为LabVIEW。

图6 实验装置

4个传感器按照四边形边长为60 mm的正方形排列。实验时，尼龙罐内空气相对压力为100 kPa。设4个传感器的坐标分别为A(-30,30,0)，B(30,30,0)，C(30,-30,0)，D(-30,-30,0)(单位为mm)。将泄漏点固定在距离传感器面不同距离的不同位置，然后分别使用TDOA、ED与本研究提出的基于数据融合的定位算法估计泄漏点位置。实验将泄漏点固定于S1(-10,70,300)，S2(-80,50,500)，S3(-20, -20,800), 3个位置。本研究将泄漏点位置计算结果的误差定义为结果与实际泄漏点位置的三坐标差值的平方和根，也即是：

(17)

式中，e为位置结果误差;xe,ye,ze为定位算法计算得到的泄漏点位置，不同算法的计算结果误差如表1所示。

表1 不同算法的实验误差

如表1所示，基于Kalman滤波的数据融合定位算法的精度明显高于ED定位算法、TDOA定位算法，这主要是因为ED算法在容器压力较低的情况下，声压比接近于1，因此该算法对误差极为敏感，定位精度一直不高，为计算带来了困难；而TDOA算法的实验误差在一般情况下是较小的，但有时会突然变得非常大，实验误差很不稳定。这是由于该算法主要是通过计算2个信号的相位差从而得到时间差，当测试距离过大时，不能准确得到相位差为θ或是(θ+360°·n)(n为任意自然数)，当估计结果与真实结果相差整整一个周期时，实验误差达到了340.28 mm。基于Kalman滤波的数据融合定位算法克服了两种算法的局限性，结果误差小于20 mm。

6 结论

本研究针对基于超声波的气体泄漏检测与定位，提出了一种基于Kalman滤波的的泄漏点定位算法，设计了一套基于该算法的泄漏定位装置并利用该装置验证了所提出的算法。本研究的创新点在于将平面四元阵应用于超声波泄漏检测定位中；设计到达时间差算法和能量衰减算法在平面阵上的定位计算模型；关联两种算法的特征向量进行泄漏点的位置估计，即将数据融合应用于泄漏点定位。实验结果表明，本研究提出的定位算法能计算出泄漏点位置，结果误差小于20 mm。

同时，该方法也存在一定的局限性。首先，在泄漏信号较小的情况下，定位系统受到环境噪声的影响较大，难以检测到气体泄漏，因此，需要改进放大滤波电路。此外，我们正在计划增加传感器阵列上的传感器数量，并研究传感器阵列的布局模式对定位结果的影响，以找到进一步提高定位系统精度的方法。