3D脑肿瘤分割的Dice损失函数的优化

刘昊，王冠华，章强，李雨泽，陈慧军

清华大学 医学院 生物医学工程系，北京 100084

引言

脑肿瘤是致命的疾病之一，全球每年发生原发性脑瘤的人数约为250000人，而脑瘤平均五年存活率为33%[1]。为了提高病人的生存率，尽早提供积极有效的治疗有着重要的意义。仅对于临床常见的脑胶质瘤来说，高级别胶质瘤（High-Grade Glioma，HGG）病人的生存率较低。然而，通过对胶质瘤的低级别（Low-Grade Glioma，LGG）早期阶段进行精确诊断，就可以较好的延长病人的寿命[2-3]。因此尽早地对脑肿瘤进行精确诊断十分重要。

磁共振成像（MRI）作为一种重要的临床脑肿瘤成像技术可以为医生的临床诊断提供重要信息[4]。脑肿瘤在磁共振图像上有着较为明显的对比度，利于对脑肿瘤进行准确的分割。准确地分辨脑肿瘤对于其诊断、治疗和术后追踪有着重要的意义，然而在临床应用中，目前主要使用手动分割的方法来分割脑肿瘤，费时费力，且可重复性较差。因此全自动高准确度的脑肿瘤分割算法对临床的准确诊断和脑肿瘤的治疗有着非常重要的意义。目前，国际上很多研究者进行了磁共振脑肿瘤分割的研究。使用神经网络对医学图像进行分割源自Ronneberger等[5]提出使用UNet对2D医学图像进行分割，采用V-Net对3D图像进行分割并使用Dice系数作为损失函数，使得网络可以优化更加直接。Kamnitsas等[6]使用交叉熵损失函数作为损失函数，训练了deep medical，FCN[7]和 3D UNet的集成学习模型用来分割脑肿瘤[8]。Szegedy等[9]提出利用肿瘤区域之间的包含关系来进行顺序分割，并提出了类似于Inception Network的思路[10]，采用了3×3×1和1×1×3卷积核来替代3×3×3的卷积，既可以节约计算时间又可以减少GPU显存的使用。Isensee等[10]提出采用通用3D UNet模型和额外的数据进行分割，并使用了均值Sorensen Dice 损失函数+交叉熵损失函数作为损失函数。Huang等[11]使用DenseNet作为UNet编码器并且利用3×3×3空洞卷积替代无空洞卷积以提高网络视野域得到更好结果。Andriy Myronenko等人额外添加一个自动解码器对应到原图，然后使用原图和真实图（Ground Truth）所对应的均值Jaccard损失函数+KL divergence损失函数作为损失函数以得到更好的结果[12]。

以上研究方法均优化训练集标签所提供标签，本研究在端对端的卷积神经网络上提出了一种新的代价函数来提高分割的准确率。该代价函数在融合均值Sorensen Dice代价函数和交叉熵函数的基础上[10]，进一步融合了全肿瘤区，核心肿瘤区这两个重要临床分割目标的Dice系数。在实际测试中，本研究还对比了现有的其他代价函数，证实了新提出的代价函数有更高的分割准确率。

1 方法

1.1 数据

本文采用Brats2018数据集[2-3]，包括285例病人，其中210例为高级别胶质瘤（HGG），75例为低级别胶质瘤（LGG）。每例病人的数据包括四个分辨率为240×240×155的刚性配准过的3D磁共振序列（T1，T1Gd，T2和T2 Flair）图像和相对应的手动标记的“真实”分割结果（Ground Truth）。该数据集来自19个机构使用不同的磁共振扫描仪所获得的数据，标记数据主要包括四个部分：背景（Background（BG），类型0）、坏死核心区和非增强核心区（Necrotic and non-Enhancing Tumor Core，NC&NETC，类型1）、水肿区（Edema，ED），类型2）和增强核心区（Enhanced Tumor，ET，类型 3），

1.2 数据预处理

数据的标准化：首先使用训练集的数据统计多对比度数据每个序列的均值和方差，然后利用统计的均值和方法分别对多对比度数据的每个图像进行零均值化和单位方差操作。

数据增值：首先采用随机旋转0°、随机旋转90°、180°、270°、随机翻转和0.9～1.1倍的随机尺度变换。再采用随机切割的方法分别将多对比度数据（配准的大脑 3D T1、T1Gd、T2和 T2 Flair数据）分成多对比度的4×128×128×128的小块数据[9]。

1.3 神经网络

本研究分割网络使用的是基于改进版本的端对端的3D UNet神经网络[13]作为分割网络，主要结构由编码器和解码器组成。其中编码器主要由下采样模块（down sample）和带残差下采样卷积模块（dconv block）构成，而解码器主要由上采样模块（up sample）和带残差的上采样卷积模块（uconv block）组成。相比于传统的3D UNet，不仅融合了前面的低尺度信息，同时使用上采样模块和卷积操作和解码器上一层信息进行叠加以融合更多的多尺度信息，分割层（seg layer）步幅为1的1×1×1的卷积操作，每层的输出的通道数都为4。最后网络通过softmax激活函数进行输出，整体网络结构如图1所示，其中每个部分的详细设计在1.3.1和1.3.2中详细介绍。

图1 脑肿瘤神经网络结构分割图

1.3.1 编码器

编码器主要由第一层卷积、下采样模块（down sample）和带残差的下采样卷积模块（dconv block）构成。第一层卷积采用步幅（Stride）为1卷积核的个数（Number of Filter）为使用16的3×3×3的卷积，随着每次下采样卷积核个数进行加倍。下采样模块为步幅为2的Max Pooling模块。带残差的下采样卷积模块采用了类似ResNet的操作，主要由卷积，群标准化方法（Group Normalization，GN）[14]和激活函数构成，具体如图2a所示。

图2 编码器

1.3.2 解码器

解码器由上采样模块（Up Sample）和带残差下采样卷积模块（uconv block）构成，其中上采样模块由三维的双线性插值上采样（3D Bilinear Upsampling）模块组成。而uconv模块如图2b所示。为了更好地利用多尺度的信息，除了合并前面的低尺寸信息之外，Modified UNet额外增加了一条通道，其中分割层（seg layer）由步幅为1的1×1×1的卷积核构成，输出的卷积核个数为四个，如前所述，四个通道类别代表：背景1、坏死核心区2和非增强核心区3、水肿区和增强核心区4，其中通道1+2+3为全肿瘤区（Whole Tumor，WT）：通道1+通道2+通道3），通道 1+3 为核心肿瘤区（Tumor Core，TC）：通道 1+ 通道 3），见图3。

图3 通道说明图

1.4 损失函数

本文提出新的损失函数主要由三部分组成：交叉熵损失函数（Cross Entropy，CE））、均值 Sorensen Dice 损失函数[10]和直接优化项的Sorensen Dice损失函数。交叉熵损失函数和Sorensen Dice[15]损失函数分别如公式(1)、(2)所示，其中p(x)为预测值而q(x)为相对应的真值，其中p(x).sum()为p(x)中所有值相加，eps=1.0。

在本研究的实际问题中，损失函数的第一部分是由均值Sorensen Dice损失函数Sorensen_Dice_NETC_ED_ET组成，具体见公式(3)所示。其中LNETC、LED和LET分别为其为NC&NETC、ED、ET的 Sorensen Dice损失函数构成。

在实际问题中，新提出的损失函数的第二部分主要由交叉熵损失函数构成，具体见公式1。在融合了均值Sorensen Dice损失函数和交叉熵损失函数这两部分之后，就可以得到损失函数Sorensen_Dice_NETC_ED_ET_CE，具体如公式(4)所示。

由于以上目标函数在优化的时，都未考虑TC、WT此两项，而是间接优化NETC、ED、ET，所以本文新提出的损失函数的第三部分主要由直接优化项组成，试图优化临床所需的TC和WT。即在公式(4)（Sorensen_Dice_NETC_ED_ET_CE）的基础上加上以上分割目标的Sorensen Dice损失函数得到最终的优化函数Sorensen_Dice_NETC_ED_ET_WT_TC_CE，见公式(5)，其中LWT和LTC分别全肿瘤区，核心肿瘤区的Sorensen Dice损失函数，具体如图3所示。

1.5 优化器

本文使用Adam优化器，权值衰减使用为1e-5，使用步衰减学习率（step learning rate）。总共 450 个时期（epoch），初始学习率为1e-4，衰减率gamma等于0.5，前400个100个时期衰减一次。后面50个时期每25个epoch衰减一次。批尺寸（batch size）为 2。

1.6 训练与测试

本文使用 Pytorch 并在 NVIDIA Titan XP 12GB GPU 上完成训练与测试。我们将训练集HGG和LGG两种情况分别按照4:1的比例分为训练集和测试集。本文将原尺寸图片240×240×150填补（padding）到240×240×160输入神经网络进行测试。本研究的评价的指标为：WT区为1:+2+3，TC区为1+3和ET区为3的Sorensen Dice系数。

作为对比，本文还比较了两种现有的代价函数。首先对比了Sorensen Dice函数和Jaccard Dice函数所对应的均值Sorensen Dice函数和均值 Jaccard Dice损失函数[13]（Jaccard_Dice_NETC_ED_ET：公式(7)。

其中LJaccard_Dice_NETC、LJaccard_Dice_WT和LJaccard_Dice_ET分别为NETC、WT、ET的Jaccard损失函数。

为了测试背景在均值Sorensen Dice损失函数中是否重要，还对比了Sorensen_Dice_NETC_ED_ET损失函数和添加背景的均值Sorensen Dice损失函数（Sorensen_Dice_NETC_ED_ET_BG），见公式 (8)。

2 结果

相比于交叉熵的损失函数和均值Sorensen Dice损失函数，本文提出的新损失函数Sorensen_Dice_NETC_ED_ET_WT_TC_CE在三项指标（肿瘤区、肿瘤核心区和增强肿瘤区）上均在测试集上取得了最佳准确率（表1），分别在肿瘤区、肿瘤核心区和增强肿瘤区这三个目标区域的平均Dice系数分别达到：0.875、0.829、0.695。

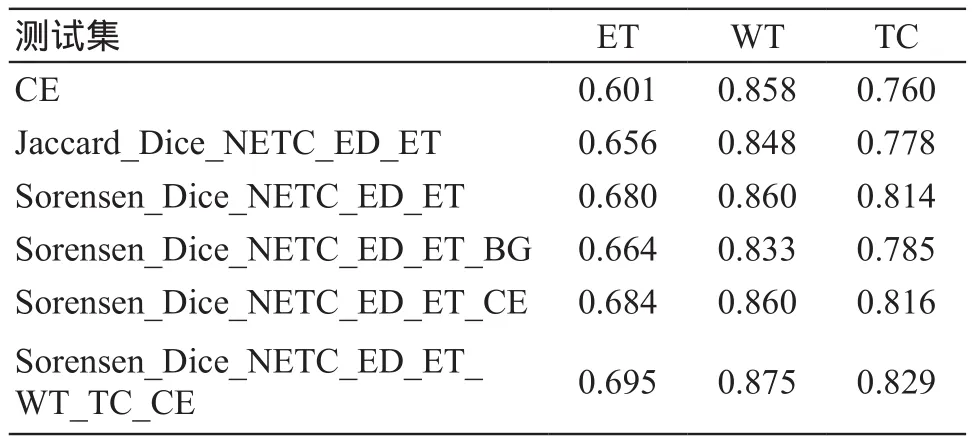
表1 测试集结果

另外，在均值Jaccard Dice损失函数（Jaccard_Dice_NETC_ED_ET）和均值Sorensen Dice损失函数（Sorensen_Dice_NETC_ED_ET）损失函数的对比中，均值Sorensen Dice损失函数在WT、TC、ET三个指标上都取得了领先的结果。尽管交叉熵损失函数（CE）在结果上不如均值Sorensen Dice损失函数（Sorensen_Dice_NETC_ED_ET），但是组合这两者得到Sorensen_Dice_NETC_ED_ET_CE的结果相对于单独使用两者都可以得到一定的提升。而在背景项（BG）意义的测试中，加入背景项Sorensen_Dice_NETC_ED_ET_BG的分割准确率低于不加背景项均值Sorensen Dice 损失函数。

本文提出的Sorensen_Dice_NETC_ED_ET_WT_TC_CE损失函数与Sorensen_Dice_NETC_ED_ET_CE和CE损失函数的收敛曲线对比图，见图4。可以看出，使用交叉熵损失函数（CE）的神经网络收敛曲线震荡较大且收敛速度慢，而使用新提出的Sorensen_Dice_NETC_ED_ET_WT_TC_CE损失函数与Sorensen_Dice_NETC_ED_ET_CE代价函数的神经网络相比，在收敛速度基本相同的情况下获得了更好的结果。

图4 测试集收敛曲线

两例病例的分割结果对比图，见图5，包括使用CE代价函数的分割图（图5c）、使用Sorensen_Dice_NETC_ED_ET_CE代价函数的分割图（图5d）、使用本文提出的新的Sorensen_Dice_NETC_ED_ET_WT_TC_CE代价函数的分割图（图5e），以及原图（图5a，选取Flair序列作为原图）和人工分割的真实图（图5b）的对比。可以发现，使用三种不同的代价函数的神经网络所获得的分割结果在整体WT上分割的结果较为相似。然而在TC和ET上的分割结果相差甚多，本文所提出的Sorensen_Dice_NETC_ED_ET_WT_TC_CE代价函数所获得的分割图不管是在ET和TC的分割上，还是在ED和NETC的分割上均最接近真实图结果。

图5 分割结果图

3 讨论

本文提出了融合均值Sorensen Dice函数、交叉熵函数和目标分割区域代价函数的新损失函数，可直接在神经网络中优化对于临床非常重要的全肿瘤区、核心肿瘤区、增强肿瘤区评价指标的Dice系数。相比于传统的交叉熵损失函数和均值Sorensen/Jaccard损失函数，使用该损失函数的神经网络可以得到更加准确的分割结果。本文中的方法与Rahman等[16]提出直接使用IOU损失函数作为损失函数来优化神经网络的思想有相似之处，但本文采取不同的方式，将直接需要优化项目标项加入到已有的均值Sorensen损失函数。本研究的结果也表明，在分割不同种类的目标时，针对主要分割目标进行代价函数的设计有可能得到更准确地分割结果。

另外，本研究结果表明，在均值Sorensen Dice函数中加入背景优化，反而会导致目标分割的准确性下降。可能的原因是，在Brats2018的数据集中，坏死核心区和非增强核心区，水肿区，增强核心区样本之间在训练集的像素比例为：25%、57%和18%，相对比较平衡，而BG和NETC+ED+ET像素比例接近90，导致神经网络更加倾向于背景信息的优化，导致其他项在损失函数中变得不重要，最终严重影响了最终分类的准确率。

在WT、TC、ET这三个分割目标中，可以发现不管使用哪种代价函数，ET的分割准确率都是最低的。这不仅是因为ET相对于其他组织的对比度较差，而且由于图像采自于不同的设备，导致不同图像的ET对比度不尽相同，需要网络有很强的泛化能力才能得到精确的结果，我们接下来的工作将会集中在如何提高网络的泛化能力，使得网络能够更好地契合不同机器采集的图像以得到更好的结果。