基于GA-BP神经网络模型的交通流量预测

王小凡 朱永强

（青岛理工大学机械与汽车工程学院，山东 青岛 266520）

近年来我国汽车保有率迅速上升，交通建设逐步完善，高速公路成为越来越重要的出行方式，高速公路不仅为出行提供许多便利，它还加快了周边地区的经济发展。但是随着交通事业的飞速发展，高速公路上交通量猛增，甚至超出了道路通行能力造成交通拥堵和连环事故，为了提高道路的通行效率，需要对高速公路的交通量进行分类控制和合理诱导，而准确的交通量预测则是进行科学交通规划和诱导的前提和关键。

随着智能交通迅速发展，交通量预测作为智能交通系统的关键因素引起了越来越多的学者关注，先后提出了很多模型运用到实际交通量预测中，如学者Smith和Oswald在2002年提出非参数回归模型，[1-2]学者Castro等创立了一种支持向量机预测模型，[3-4]学者Okutani根据卡尔曼滤波理论建立了交通流预测模型以及神经网络等预测方法。[5]国内研究者周小鹏、冯奇等提出基于最近邻法的短时交通流预测。[6]

目前人工智能已经成为当下的热点方向，神经网络可以模拟人脑信息处理的过程，具有高度自主学习性和信息处理能力，已经在许多领域进行实际的运用，[7]非常适用于解决非线性、复杂的交通系统问题，但是神经网络自身也存在收敛速度慢，容易陷入局部极小的缺陷，造成预测误差。因此本文根据道路交通特点结合实际情况，提出用遗传因子优化小波神经网络，建立一种遗传算法优化BP神经网络预测模型，使得神经网络可以迅速找到最优解并提高预测精度。

1 BP神经网络

BP（Back Propagation）神经网络是一种多层前馈神经网络，[8]由输入层、输出层和隐含层构成，每一层由若干节点连接，输入信号从输入层经隐含层逐层处理并传向输出层，若输出层结果与期望输出相比误差过大，则将误差信号沿输出层反向传递，逐层修改和调整连接权值和阈值，反复迭代直至输出结果和期望结果误差满足一定条件，BP神经网络的拓扑结构如图1所示：

图 1 BP神经网络拓扑结构图

图中，X1，X2，X3，…Xn为 BP 神经网络的输入值，Y1，Y2，Y3，…Yn是预测值，ωij和ωjk为连接权值。

1.1 训练过程

（1）BP神经网络首先需要经过网络训练，假设神经网络输入层节点数n、隐含层节点数l、输出层节点数m、连接权值ωij，ωjk等，初始化网络，然后计算隐含层输出。

（2）计算神经网络预测输出O：

BP神经网络凭借自身的较强的自学习、自适应、容错性的优点已被广泛应用于信号识别、系统优化等领域中，但是传统的BP神经网络也呈现出收敛速度较慢，陷入局部最优以及全局搜索能力不足的缺陷，使得BP神经网络在预测应用中预测精度仍不能满足需求。

2 遗传算法优化BP神经网络模型建立

2.1 遗传算法

美国Michigan大学Holland教授在1962年根据自然界中物竞天择的机制以及各种生物进化规律提出遗传算法（Genetic Algorithms），这种算法主要是在计算模型中设定成生物自然地进化竞争的机制，编码模型中问题参数成染色体，模拟自然界中生物遗传的选择，交叉和突变过程，并根据健康状况保留具有良好适应值的优秀个体，遗传算法具有自适应随机优化搜索，可以做到全局寻优，在最优化领域方面更加成熟，收敛速度和效果更好。

GA-BP网络预测模型首先确定BP神经网络结构，根据拟合函数输入和输出参数来确定遗传算法个体的长度。使用遗传算法找寻网络最优适应值，使用新的权值和阈值训练BP神经网络并输出预测结果。[9]

2.2 GA-BP网络实现步骤

（1）数据处理

对原始样本数据进行预处理作为神经网络的输入。

（2）确定BP网络结构

随机初始化BP神经网络的权值和阈值

（3）初始种群进行编码

传统二进制编码存在连续函数离散化的映射误差，实数编码更适合应用于多维数值问题，使得遗传算法更加接近待解问题空间，对于个体较多的神经网络，用实数对每个个体编码，获得初始种群。

（4）适应度函数

个体适应度值F是指根据个体预测输出与实际输出之间的误差绝对值和，计算公式为：

式中，n为网络输出节点数；yi为网络的第i个节点的实际输出；oi为第i个节点的预测输出；k为系数。

（5）选择操作

确定随机选择个体的概率与其适应度函数值成正比，遗传算法选择轮盘赌法（Roulette Wheel Selection）：

其中Fi是第i个个体的适应度值；k为系数；N为种群个体数。

（6） 交叉操作

交叉是将上代中优秀的基因组合传递至下一代，在两个个体中随机选取一个基因位置作为交叉位置，组成新的优秀个体，产生新的寻优空间[10]：

式中，b是[0，1]间的随机数。

（7）变异操作

将变异算子作用于群体，提高遗传算法局部随机搜索能力，并保持种群的多样性。选取第i个体的第j个基因αij进行变异操作：

式中，γ2为随机数；g为网络已迭代次数；Gmax为网络最多进化次数；αmax，αmin分别为基因αij的上界和下界；r为[0，1]间的随机数。

（8）判断网络是否完成参数优化

如果网络预测结果不满足期望误差值和迭代次数，则返回重复迭代，如果达到，则输出最优染色体。

（9）构造训练网络

优化后的初始权重和阈值从GA算法部分获得并分配给BP网络并构建网络。

3 实例分析

本次实验数据来源于辽宁省某高速公路2015年全年日交通量，共365组数据，将每5组数据分为一组，获得71组数据，使用61组数据作为训练样本，剩余10组作为测试样本。

设置GA-BP神经网络结构为4-6-1，即将神经网络结构设置为3层，其中输入层为4，输出层1，隐含层5，共有4×5+5×1=25个权值，5+1=6个阈值。GA-BP神经网络学习概率为0.1，隐层激励函数用tan-sigmoid，输出层的激励函数是linear，训练函数是traingd.网络中种群数目为10，遗传迭代次数10，交叉概率为0.3，遗传概率为0.1，误差精度为0.001。

3.1 预测结果分析

为了验证遗传算法优化BP神经网络（GA-BP）在交通量预测中的效果，使用相同网络结构的传统BP神经网络对同一样本数据做出预测，使用平均相对误差（MAPE），均方根误差（RMSE）两种评价指标对遗传算法BP神经网络（GA-BP）与传统BP神经网络预测结果进行评价和比较：

使用两种预测模型进行训练网络并预测，输出结果见表1，图2和图3

表1 预测评价指标对比

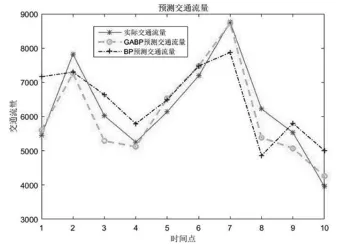
图2 两种神经网络预测结果对比图

图3 两种神经网络MAPE对比

从表1可以看出，GA-BP两项评价指标均优于传统BP算法，误差较后者比有明显下降，表明引入遗传算法后提高了全局搜索能力，预测精度得到显著提升。根据图2可知，虚线代表的GA-BP神经网络预测交通量曲线更贴实际交通量的实线，与实际交通量的变化趋势相符。图3表明BP预测误差有较大波动，而GA-BP的误差曲线趋势则较为平缓，由此可知由遗传算法改进的GA-BP神经网络预测值更贴近实际值，预测精度优于传统BP神经网络。

4 结论

本文提出的基于GA-BP算法的交通量预测方法将BP网络初始权重和阈值优化引入生物进化中的自然选择和交叉变异算子。利用遗传算法的全局搜索能力，寻找BP神经网络的最优权值和阈值，有效地缩小了预测模型寻优参数的取值范围，使得优化后的BP神经网络获得更快的收敛速度从而提高预测精度。采用辽宁省某高速公路全年日交通量作为原始数据，预测交通量，实验数据表明传统BP神经网络预测结果相对误差为13.17%，而GA-BP神经网络预测相对误差为6.81%，后者预测误差较小在可接受范围之内，而且精度更高更加贴近实际值，结果证明该预测算法具有更快的收敛速度以及更加准确的预测结果，整体预测准确度得到了提高，克服了传统BP神经网络容易陷入局部最优的缺点，可以为交通预测、规划等相关工作提供一定的参考价值。