一种适用于LT码的选择编码算法

宋鑫 廖育荣 丁丹

摘  要： 无速率码的出现为自适应数据传输提供了新途径。作为第一种实用的无速率码，LT码在高斯信道中的性能不佳，存在较高的误码平台。针对此问题，提出一种选择编码（SE）算法。SE算法按照度数值大小将信息节点分类成若干个集合，并通过控制编码过程使每个校验节点优先从小度数值节点集合中选取与之相连接的信息节点，从而消除了小度数值的信息节点，降低了LT码的误码平台。通过蒙特卡洛仿真得到不同条件下SE算法中信息节点的度分布，并利用外信息传递图法对SE算法及传统编码方法的收敛性进行对比分析，结果显示SE算法能够进一步拓宽译码通道，使误比特率更快趋近于0。此外，SE算法在给定范围信噪比及码率值条件下均能降低误码平台，当误比特率为10-5时，码长为512 bit的LT码可以得到近5 dB的性能改善。

关键词： 信道编码; LT码; 高斯信道; 编码算法; 外信息传递; 收敛性

中图分类号： TN911.22?34                    文献标识码： A                        文章编号： 1004?373X（2019）12?0001?06

Abstract： The emergence of the rateless code provides a new way for adaptive data transmission. As the first practical rateless code， the LT code has a poor performance and high error floor in the Gaussian channel. Therefore， a selective encoding （SE） algorithm is proposed. In accordance with the degree values， information nodes are sorted into several sets by the SE algorithm. The encoding process is controlled to enable each check node to preferentially select the information node connecting with it from the small degree node sets， so as to eliminate small degree information nodes and decrease the error floor of the LT code. The degree distributions of information nodes in the SE algorithm under different conditions are obtained by the Monte-Carlo simulation. The convergences of the SE algorithm and conventional encoding algorithm were compared and analyzed by using the extrinsic information transfer （EXIT） chart method. The results demonstrate that the SE algorithm can further expand the decoding channel， make the error bit rate approach zero faster， decrease the error floor with a given range of SNRs and bit rate values， and make the LT code of 512 bit length achieve performance improvement of about 5 dB when the error bit rate is 10-5.

Keywords： channel coding; LT code; Gaussian channel; encoding algorithm; extrinsic information transfer; convergence

0  引  言

作为一种特殊的信道编码，无速率码[1]最初应用于二进制删除信道（Binary Erasure Channel，BEC）中以提高数据传输效率。LT码[2]是第一种实用的无速率码，Raptor码[3]则是以LT码为内码、高码率的预编码为外码的级联无速率码。无速率码在BEC中具有优良性能，文献[4?5]证明，经过恰当设计，无速率码也可以应用于加性高斯白噪声（Additive White Gaussian Noise，AWGN）信道中。

LT码在AWGN信道中存在较高的误码平台，而Raptor码中的外码能够进一步纠正LT码的错误，因此Raptor码的误比特率（Bit Error Rate， BER）能随着编码长度的增加瀑布式下降，但这是以高编译码复杂度为代价的[6]。实际上，作为无速率码的核心，LT码的性能直接影响着无速率码的性能及实用性，而对LT码性能造成直接影响的是LT码的编码方式和校验节点度分布函数。因此，文献[7?8]考虑对LT码的编码过程进行改进以提高其性能。此外，LT码的度分布函数的设计方法也在不断优化改进，如基于联合译码算法和外信息传递（Extrinsic Information Transfer，EXIT）圖法的设计方法[9];基于多边网络结构的设计方法[10?11];基于译码“波纹”的设计方法[12];基于分类信息节点的设计方法[13]等。然而，上述文献均是从LT码校验节点度分布的角度出发，通过优化LT码自身结构以提高BER性能，未能从信息节点的角度出发考虑信息节点度分布对LT码性能的影响。此外，大多数文献均是将LT码作为Raptor码的一部分进行联合设计，未能单独针对AWGN信道中的LT码进行改进。LT码作为Raptor码的核心，如果能提高LT码的性能，实际上就相当于提高了Raptor码的性能。

针对上述两个问题，本文提出一种适用于LT码的选择编码（Selective Encoding，SE）算法。该算法通过改变编码过程中校验节点选择信息节点的方式，优化了LT码的信息节点度分布，从而改善了LT码的误码平台现象。首先，从信息节点的角度出发分析了造成LT码误码平台现象的原因，得到随机选择信息节点的方式并不是最优编码方式，并通过仿真证明移除小度数值的信息节点有助于提升LT码的BER性能。因此，本文提出的SE算法按照度数值大小将待编码的信息节点分类，在每生成一个校验节点时会优先从小度数值节点集合中选取信息节点，从而消除了小度数值的信息节点。进一步利用EXIT图法对SE算法及传统编码方法的收敛性进行对比分析，验证了SE算法的有效性。另外，SE算法没有改变校验节点度分布，因此，算法的译码复杂度与传统方式相当。最后，AWGN信道中的仿真结果显示，SE算法能够在大范围信噪比及任意码率条件下均实现BER性能的提升。

1  LT码

1.1  LT码的编码

在LT码中，对包含K个信息比特的向量[v=v1，v2，…，vK]编码产生包含N个编码比特的向量[w=w1，w2，…，wN]。每产生一个编码比特[wj1≤j≤N]时，首先根据度分布函数[Ωx]依概率生成一个度数值d，然后从K个信息比特中随机选取d个进行异或，将结果赋值给wj。重复上述过程直至生成N个编码比特，此次编码结束。校验节点度分布函数定义为[Ωx=j=1dcΩjxj]，其中[Ωj]是选中度数j的概率，dc是最大校验节点度数值。LT码还可以用Tanner图来表示，如图1所示。其中，每个信息节点连接的边的个数即为该信息节点的度数值。定义信息节点的度分布函数为[Λx=i=1dvΛjxi]，其中，dv为最大信息节点度数值。

图1 LT 码的Tanner 图

在LT码中，定义信息节点和校验节点基于边的度数分布分别为[λx=i=1dvλixi-1]和[ρx=j=1dcρjxj-1]。[λx]满足[λx=Ω′xΩ′1]，[ρx]满足[ρx=Λ′xΛ′1]。尽管LT码是无速率码，但定义其瞬时码率为[R=KN]。

1.2  LT码的译码

在AWGN信道中，LT码采用置信传播（Belief Propagation， BP）算法进行迭代译码。该算法将对数似然比（Log?Likelihood Ratio，LLR）信息在信息节点和校验节点之间进行来回传递和更新，使LLR信息逐渐收敛于稳定值并据此进行最佳判决。令[Lcj→vi]表示迭代过程中第j个校验节点传递给第i个信息节点的LLR信息，定义为：

2  选择编码算法及其收敛性分析

2.1  LT码误码平台分析

本节从信息节点的角度出发，分析误码平台形成的原因以及改进措施。传统LT码中，随机选择信息节点的编码方式使得信息节点的度数服从均值和方差为α的泊松分布，且[α=βNK，β=j=1dcjΩj]，其中[β]为校验节点平均度数，[α]又被称为信息节点平均度数。换言之，信息节点的度分布只与校验节点度分布函数和码率倒数相关。在泊松分布下，小度数值信息节点的比例不为0，因此，无论参与编码的信息节点的个数是多少，在大量重复实验时，总会存在相当一部分的小度数值信息节点。这些小度数值信息节点连接的校验节点的个数有限，能够获得的来自校验节点的LLR信息较少，往往不足以使其准确地判断自身的状态，从而无法被正确恢复。这些可靠性较低的小度数值信息节点的存在使得LT码的BER始终无法随编码长度的增加降至为0，即造成了误码平台现象。

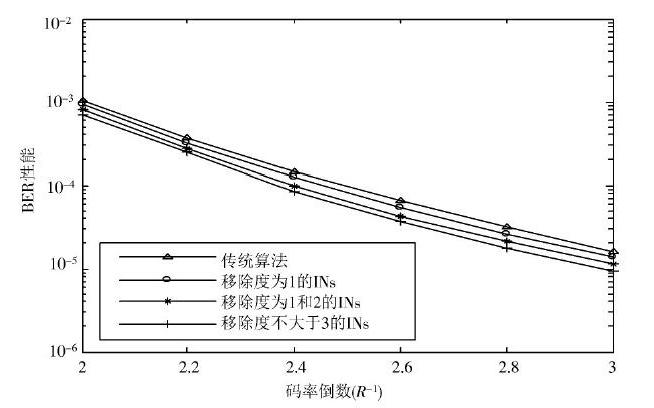
以文献[14]中给出的度分布为例，通过仿真验证小度数值信息节点对LT码性能的影响，考虑如下仿真条件：信息节点长度为[K=256]，信噪比为[EsN0=0]，譯码迭代次数设置为50。仿真对以下情况进行比较：不改变信息节点度数、移除度数为1的信息节点、移除度数为1和2的信息节点、移除度数不超过3的信息节点，结果如图2所示。显然，随着小度数值信息节点数目的减少，LT码的误码平台不断降低，这表明，可以通过移除小度数值的信息节点进一步降低LT码的误码平台。

图2 移除不同度数值信息节点时的BER 性能

综上所述，在传统编码算法中，随机选择信息节点的方式并不能使LT码的BER性能达到最优。因此，本文考虑通过改变选择信息节点的方式消除小度数值信息节点，达到提高LT码BER性能的目的。

2.2  选择编码算法

根据第2.1节的分析，提出针对LT码的选择编码算法，见算法1。算法中涉及的参数有：信息比特个数K，编码比特个数N，度分布[Ωx]。算法流程如下：

算法1中，每生成一个编码比特时都按当前校验节点度数值[d]优先选取前[d]种度数的信息节点，则在生成第[k+1]个编码比特时，度数不大于[β]的信息节点就已经不存在了。因此，算法1消除了小度数值的信息节点，并将98%以上的信息节点的度数值都集中于[α-2，α+8]区间内，提高了中等度数值信息节点的比例，从而改善了误码平台现象。另外，算法1没有改变校验节点的度分布，即校验节点与信息节点之间的平均边数仍为[Nβ]，因此译码复杂度与传统方式相当。

2.3  算法的收敛性分析

为了验证算法1的有效性，本节利用EXIT图法对算法1的收敛性进行分析。

将LT码的译码器分为信息节点译码器（IND）和校验节点译码器（CND），则LT码的译码过程可以看作LLR信息在IND和CND之间的传递更新。在第1.1节的基础上，定义函数[Jσ]为x与y之间的互信息，满足：

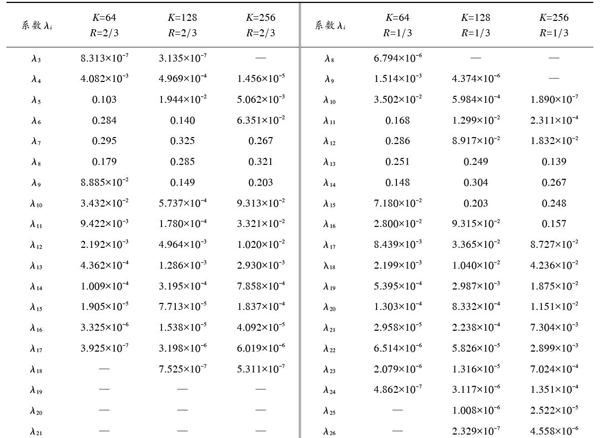
算法1对信息节点的选择方式进行了优化改进，因此，算法1中的校验节点边度数分布不变，而信息节点边度数不再服从泊松分布，即式（5）不再成立。与传统的信道编码方式不同，LT码实际上是一种基于概率选择的特殊编码，但是在算法1中，无法利用概率值的大小精确定义非空信息节点集合的个数以及每个集合中信息节点的个数，即无法利用数学理论推导算法1中信息节点边度数分布。因此，本文考虑利用蒙特卡洛仿真结果代替真實结果对算法1的收敛性进行分析。为了证明算法的普适性，表1给出了不同度分布和不同码率值条件下的仿真结果（部分），度分布采用文献[14]中针对不同码长设计的度分布，限于篇幅此处不一一列举。

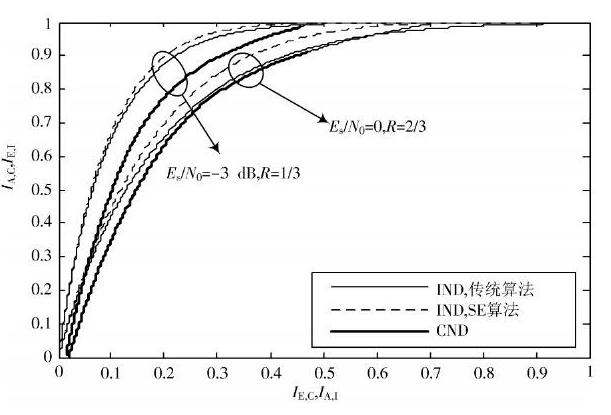
利用表1中测得的数据，绘制出K=64和K=128时的EXIT图，见图3和图4。、

图3 K=64 时的EXIT 图

CND曲线和IND曲线之间的通道称为译码通道，只有当译码通道打开，即CND曲线和IND曲线不相交且收敛于1时，BER才能趋近于0。从图3和图4中可以看出，在相同信噪比和码率值下，SE算法能够进一步拓宽译码通道，使得LT码能够在更少的迭代次数下成功译码，提高了译码效率。另外，SE算法还能在相同条件下提高译码成功概率，如在[EsN0]=0，R=[23]时，传统编码算法的IND曲线与CND曲线存在相交点，因此无论经过多少次迭代，传统LT码的BER都无法趋近于0;而SE算法的IND曲线与CND曲线之间的译码通道仍处于打开状态，因此若采用SE算法则能使LT码在有限次迭代后成功译码。

图4 K=128 时的EXIT 图

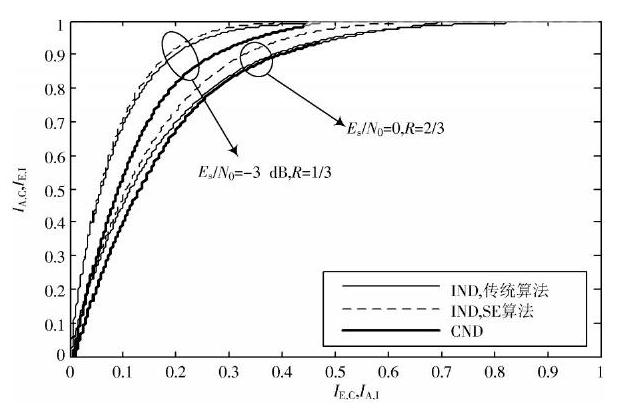
综上所述，与传统编码算法相比，SE算法能够在不同校验节点度分布、不同码率值、不同信噪比条件下均实现更为优良的收敛性，从而进一步验证了算法的有效性和普适性。

3  仿真结果及分析

表1 不同情况下信息节点边度数分布系数（部分）

本节对传统算法以及SE算法在二进制AWGN信道中的性能进行仿真对比。所有仿真结果均通过1 000 000次蒙特卡洛仿真得到，采用BP译码算法时最大迭代次数均设置为50次，LT码的码长分别为K=64，K=128，K=256，K=512，校验节点度分布与文献[14]中相同。

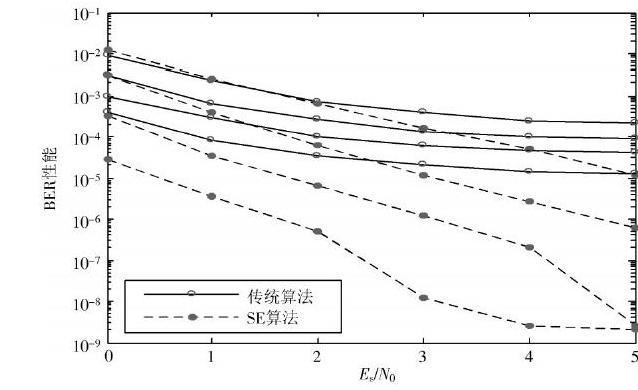
图6 R=1 2 时LT 码的BER 性能对比图

首先，在信噪比[EsN0=0]时对不同长度LT码的BER随码率变化情况进行仿真，见图5。图中实线为传统算法的结果，虚线为SE算法的结果，两种曲线从上至下分别代表K=64，K=128，K=256，K=512。可以看出，在相同条件下SE算法最多可将BER减少近2个数量级，较大程度地降低了LT码的误码平台，提高了LT码的译码成功概率，这与第2.3节对SE算法收敛性的分析结果相一致。另外，SE算法在任意码长和任意校验节点度分布下均能实现BER性能的提升，且码长越长，算法的增益越大。

其次，在固定码率[R=12]时对不同长度LT码的BER随信噪比变化情况进行仿真，见图6。图中曲线分布情况与图5相同。可以看出，SE算法极大地改善了LT码的误码平台现象。以K=512为例，传统算法在5 dB时的BER与SE算法在0时的BER相近，即SE算法能够将LT码性能提升将近5 dB。类似地，其他三种情况下的增益分别近似为2 dB，3.5 dB，4.2 dB，说明SE算法对任意范围的信噪比均能适用。

作为Raptor码实现无速率功能的关键部分，LT码性能的提升同样可以给Raptor码带来有益效果。本文在上述LT码的基础上引入码率为0.9的规则（3，30）LDPC码作为预编码，以此验证SE算法对Raptor码性能的增益。

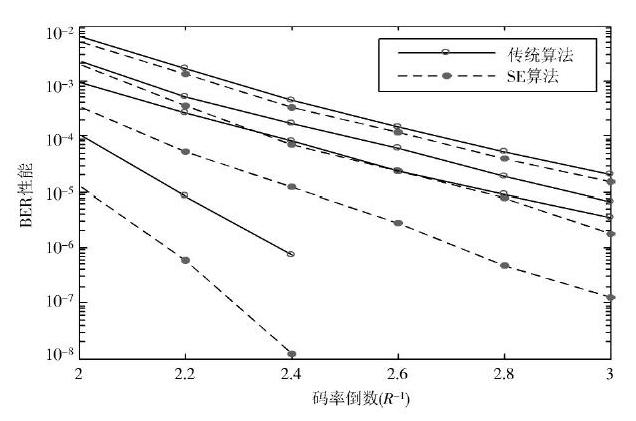
图7 Es N0=0 时Raptor 码的BER 性能对比图

为了便于分析，将信息比特长度分别设置为K=63，K=126，K=252，K=504，因此经过LDPC编码后的码字长度分别为70，140，280以及560，以便进行下一步的LT编码。LDPC码部分采用BP译码算法。

图5 Es N0= 0 时LT 码的BER 性能对比图

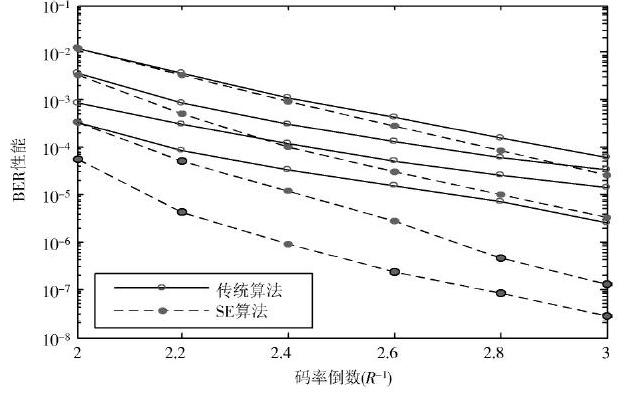
图7为上述Raptor码在信噪比[EsN0]=0时的BER仿真结果，为便于表示，横坐标仍为LT码的码率倒数（R-1）。图中4组曲线的分布情况与图5相同。可以看出，采用SE算法的Raptor码能够获得更为优良的BER性能，并且码长越长，增益越明显。以K=504的Raptor码为例，传统算法需以R-1 = 2.4的开销方能使BER达到10-6标准，而SE算法只需使R-1 = 2.2。说明SE算法能够使Raptor码以更高的码率达到相同的BER性能，从而可以在相同的时间内传输更多的有效数据，提高了数据传输效率。

4  结  语

本文从信息节点的角度出发分析了AWGN信道中LT码性能不佳的原因，进而提出一种新的SE算法。通过改变编码过程中信息节点的选择方式，消除了小度数值信息节点，并使得信息节点和校验节点之间的连接关系更加合理化，从而改善了LT码的误码平台现象。另外，本文利用EXIT图法比较了不同编码条件下传统编码算法和SE算法的收敛性，从理论上证明了SE算法的可行性和普适性。最后，仿真结果表明，无论是在LT码还是Raptor码中，SE算法均能降低BER，幅度可达1～4个数量级，且没有增加译码复杂度，从而提高了无速率码在AWGN信道中的实用性。

参考文献

[1] COSTA M， PINHO M. An algorithm for optimal unequal error protection rate allocation exploring granular channel rates [J]. IEEE communications letters， 2018， 22（5）： 926?929.

[2] LUBY M. LT codes [C]// Proceedings of the 43rd Annual IEEE Symposium on Foundations of Computer Science. Vancouver： IEEE Computer Society， 2002： 271?280.

[3] SHOKROLLAHI A. Raptor codes [J]. IEEE transactions on information theory， 2006， 52（6）： 2551?2567.

[4] YANG W， LI Y， YU X， et al. Rateless superposition spinal coding scheme for half?duplex relay channel [J]. IEEE transactions on wireless communications， 2016， 15（9）： 6259?6272.

[5] CHEN H， MAUNDER R G， MA Y， et al. Hybrid?ARQ?aided short fountain codes designed for block?fading channels [J]. IEEE transactions on vehicular technology， 2015， 64（12）： 5701?5712.

[6] ALBAYRAK C， SIMSEK C， TURK K. Low?complexity early termination method for rateless soft decoder [J]. IEEE communications letters， 2017， 21（11）： 2356?2359.

[7] HUSSAIN I， XIAO M， RASMUSSEN L K. Error floor analysis of LT codes over the additive white Gaussian noise channel [C]// Proceedings of 2011 IEEE Global Telecommunications Conference. Kathmandu： IEEE， 2011： 1?5.

[8] 姚渭箐，易本顺.基于存储机制的LT码编译码方法[J].系统工程与电子技术，2018，40（1）：165?170.

YAO Weiqing， YI Benshun. Memory?based encoding and decoding of LT codes [J]. Systems enginerring and electronics， 2018， 40（1）： 165?170.

[9] SHIRVANIMOGHADDAM M， JOHNSON S. Raptor codes in the low SNR regime [J]. IEEE transactions on communications， 2016， 64（11）： 4449?4460.

[10] JAYASOORIYA S， SHIRVANIMOGHADDAM M， ONG L， et al. Analysis and design of raptor codes using a multi?edge framework [J]. IEEE transactions on communications， 2017， 65（12）： 5123?5136.

[11] JAYASOORIYA S， SHIRVANIMOGHADDAM M， ONG L， et al. Raptor codes for higher?order modulation using a multi?edge framework [J]. IEEE wireless communications letters， 2017， 7（1）： 110?113.

[12] SORENSEN J H， KOIKE?AKINO T， ORLIK P， et al. Ripple design of LT codes for AWGN channel [C]// Proceedings of 2012 IEEE International Symposium on Information Theory. Cambridge： IEEE， 2014： 1757?1761.

[13] KHAREL A， CAO L. Improved fountain codes for BI?AWGN channels [C]// Proceedings of 2017 IEEE Wireless Communications and Networking Conference. San Francisco： IEEE， 2017： 1?6.

[14] ZHANG W， HRANILOVIC S， SHI C. Soft?switching hybrid FSO/RF links using short?length raptor codes： design and implementation [J]. IEEE journal on selected areas in communications， 2010， 27（9）： 1698?1708.