一阶弹性波交错网格时间高阶差分格式及稳定性分析
田雪丰
(中国煤炭地质总局地球物理勘探研究院,河北 涿州 072750)
基于有限差分法的弹性波模拟或成像处理[1-7],受差分格式稳定性条件的限制,每种差分格式的时间步长和空间步长的比值(简称时空步长之比)都被限制在一定范围内。为了精细地对复杂地质模型的地震响应进行数值模拟,要求空间网格步长足够小。因此,受限于差分格式的稳定性要求,必须选取小的时间步长。时间步长越小,则计算的时间步数越多,计算效率越低。
基于交错网格的一阶弹性波方程数值求解技术[1-2,4,6,8]相比于二阶弹性波方程,由于具有频散小,收敛速度快的优点,在弹性波的模拟和偏移中得到了广泛应用[8-13]。稳定性条件是交错网格差分算法的重要研究内容[2,6,13],Virieux[14]首先给出了三维情况下各向同性介质中一阶弹性波方程的交错网格的时间2阶、空间2阶差分格式的稳定性条件。Levander[15]在Virieux的基础上发展了一阶弹性波交错网格的差分格式,提出交错网格的空间差分格式可以为任意精度,并给出了时间2阶精度、空间4阶精度的差分格式及其稳定性条件。此后,高阶空间精度的差分格式广泛地应用于一阶弹性波交错网格。
董良国[8]通过将速度(应力)对时间的导数转化为应力(速度)对空间的导数,使时间高阶导数的计算在一个时间层内完成,在不增加计算所需内存的前提下,得到了任意阶时间精度和空间精度的差分格式。
本文通过标准傅立叶分析得到了这种任意阶时间精度的差分格式的稳定性条件,并提出一种将不同阶数的时间导数转换为不同精度的空间差分的时间高阶差分方法。本文的稳定性分析结果指出:在一阶弹性波交错网格中,时间高阶差分格式比时间2阶差分格式的稳定性条件更宽松,因而可以提高时空步长之比,减少数值模拟的时间步数。此外,本文指出,由于空间差分引起的数值频散是由空间上的网格离散造成的,而时间差分引起的数值频散是由时间上的网格离散造成的,两者来源不同。因此时间精度的提高不能减小空间差分引起的数值频散,压制频散时要根据频散的来源进行压制。
1 一阶弹性波速度应力方程
在不考虑体力情况下,各向同性介质一阶弹性波速度-应力方程可写作[4,8]:
(1)
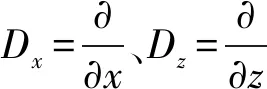
将(1)式表示为矩阵形式,有:
(2)
上式中Q为式(1)中等号右边的五阶方阵,
U(t)=[vx(t),vz(t),τxx(t+Δt/2),τzz(t+Δt/2),τxz(t+Δt/2)]T
(3)
其中Δt为时间剖分步长。
2 时间2M阶,空间2N阶差分近似
2.1 时间2M阶差分近似
应用交错网格的思想[8,13]求解一阶速度-应力方程,根据一元函数的Taylor展式,得到速度和应力的时间2M阶差分近似,以vx和τxx分量为例,有:
(4)
(5)
由此可以将(4)(5)所代表的等式联立为矩阵形式:
(6)
2.2 空间2N阶差分近似
根据交错网格思想,1阶空间导数的2N阶精度差分近似表达式如下:
(7)
其中Δx为x方向的空间剖分步长。
同理可得N方向上的1阶导数的2N阶精度差分近似为:
(8)
其中Δz为z方向的空间剖分步长。
(7)、(8)两式中的系数Cn(N)可通过将不同节点上的Taylor展式联立,利用待定系数法求解得到。
2.3 时间2M阶,空间2N阶差分格式
根据(2)式可得:
(9)
将上式代入(6)式中,得到:
(10)
将Q中的空间差分算子x和Dz用(7)、(8)两式所示的差分格式代替,则得到时间2M阶,空间2N阶差分近似表达式。
下面以时间4阶、空间4阶精度差分格式为例对上述过程进行简要说明。
根据矩阵乘法,可得:
(11)
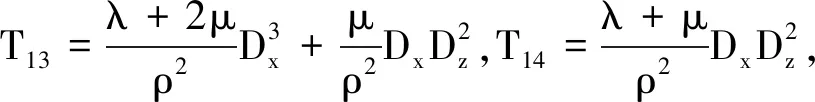
令(10)式中的时间差分精度为4阶,即M为2,得到:
(12)
将(11)式代入(12)式中,以方程形式表示,得到下列各式:
(13)
(14)
(15)
(16)
(17)
将(13)—(17)中的空间微分用空间4阶精度差分格式代替,得到时间4阶、空间4阶的一阶弹性波方程差分格式。空间1次导数用(7)(8)两式所示的差分格式进行代替,结合微分算子的乘法运算方法,可得:
(18)
(19)
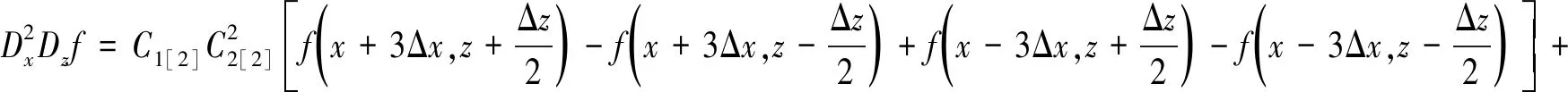
(20)
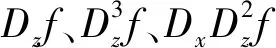
3 一阶弹性波方程交错网格二维空间稳定性分析
3.1 一阶弹性波速度-应力方程Fourier分析
对(10)式进行空间傅立叶变换,得到:
(21)
其中G(kx,kz)是Q(x,z)的傅立叶变换对。
将U(t,kx,kz)的系数矩阵记为A:
(22)
则(6)式记为
Un+1/2=Un-1/2+A·Un
(23)
式中n为时间网格序号,根据傅立叶分析方法,令:
Vn+1/2=Un
(24)
联立(22)和(23),并令:
Wn=(Un,Vn)T
(25)
可得:
(26)
(26)式中的E为单位矩阵,将式中的增长矩阵记为:
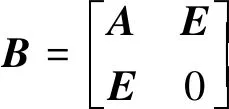
(27)
根据Von Neumann稳定性条件可知,(10)式稳定的条件是增长矩阵B的谱半径不大于1,即B的模长最大的特征值的模不大于1。
3.2 差分格式谱半径与系数矩阵A的关系
由(27)式可知,B的特征值β满足如下关系
|βE-B|=|β2E-βA-E|=0
(28)
可见β的取值与矩阵A有关,因此先求取A的特征值γ。根据(22)式,若G的特征值为η,则:
(29)
由此可见,求取A的特征值γ需要先求取G的特征值η。η满足
|ηE-G|=0
(30)
依据矩阵Q的表示形式,式(30)可写为:
(31)
式中Dkx,Dkz为空间微分算子Dx和Dz的傅立叶变换对。由(4)(5)可得:
(32)
(33)
依据行列式计算规则,(31)式简化为:
(34)
根据阿贝尔定理,对于一般的5次方程不存在用根式表达的求根公式,由(34)式可以看出,η存在一个单重根0。在不考虑0根的前提下,(34)式中可约去一个η,使η的最高阶数降为4,因此,可利用4次多项式的求解方法计算得到η的5个特征值为:
(35)
由(29)式所示的γ和η的关系,得到矩阵A的5个特征值为
(36)
由于A为5阶方阵,且有5个互异的特征值,因此矩阵A可对角化,有:
A=PΛP-1
(37)
式中P为可逆矩阵,Λ为A的特征值所构成的对角阵,即:
Λ=diag(γ1,γ2,γ3,γ4,γ5)
(38)
因此式(28)可写为:
|P(β2E-βΛ-E)P-1|=0
(39)
由于P为可逆矩阵,可以证明:
|(β2E-βΛ-E|=0
(40)
因此,B的特征值β和A的特征值γ有如下关系:
β2-βγ-1=0
(41)
解得:
(42)
由(32)、(33)、(36)式可知,γ的5个值中,有4个为无实部的复数,另外1个为0。当γ=0时,β=±1满足Von Neumann稳定性条件。当γ≠0时,令γ=ia,a为实数。若γ2+4<0,即a>2或a<-2,则β为没有实部的复数
(43)
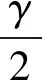
(44)
因此,当|a|≤2时,式(10)式满足Von Neumann稳定性条件。至此,得到如下结论:当(36)式所示的系数矩阵A的最大模长的特征值的模不大于2时,(10)式所示的差分格式稳定。
3.3 差分格式的稳定性条件
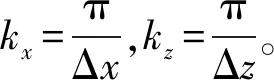
(45)
注意到空间差分系数Cn[N]在n为奇数时为正值,在n为偶数时为负值,因此可将(-1)n+1Cn[N]记为|Cn[N]|。由于弹性常数λ和μ均大于0,因此|γ1|>|γ3|,由此可知差分格式稳定的条件是:
≤1
(46)
≤1
(47)

表1 各阶差分精度的稳定性条件
表1是根据(47)式得到的部分差分格式的稳定性条件。需要指出的是,在同一个差分格式中,也可以将不同阶数的时间导数用不同精度的空间差分进行逼近,例如,在时间4阶差分格式中,将1阶时间导数利用空间4阶差分格式逼近,将3阶时间导数利用空间2阶差分格式逼近,则差分格式的稳定性条件为:
≤1 (48)
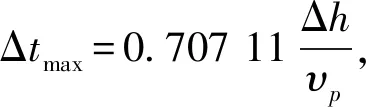
在时间6阶精度差分格式中,将1阶时间导数利用空间2阶差分逼近,将3阶时间导数和5阶时间导数利用空间4阶差分逼近,则差分格式的稳定性条件为:
≤1
(49)
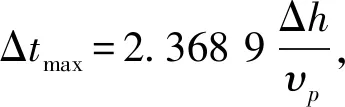
4 应用实例
4.1 时间高阶精度和时间2阶精度差分格式正演模拟
设定一个各向同性均匀介质模型,模型各项参数为:密度ρ=2 000kg/m3,纵波速度υp=2 000m/s,横波速度υs=1 300m/s。设定震源表达式为:
{1-2[πf(t-100)Δt]2}e-[πf(t-100)]2
(50)
其中f为震源子波主频,(t-100)意味着震源延迟(100Δt)ms激发。
令f=30Hz,Δh=5m,选取2阶时间精度,4阶空间精度差分格式进行正演模拟。由表1可知,满足稳定性条件的最大时间步长为0.001 51s。
令Δt=0.001 5s,计算空间401×401个网格点,震源位置(201,201),第250个采样时刻(375ms)的vx分量波前快照如图1(a);令Δt=0.001 6s,记录第250个采样时刻(400ms)的vx分量波前快照如图1(b)。可以看出,使用2阶空间精度差分格式进行正演, 当Δt>Δtmax, 数值解变得不稳定; 只要Δt<Δtmax,
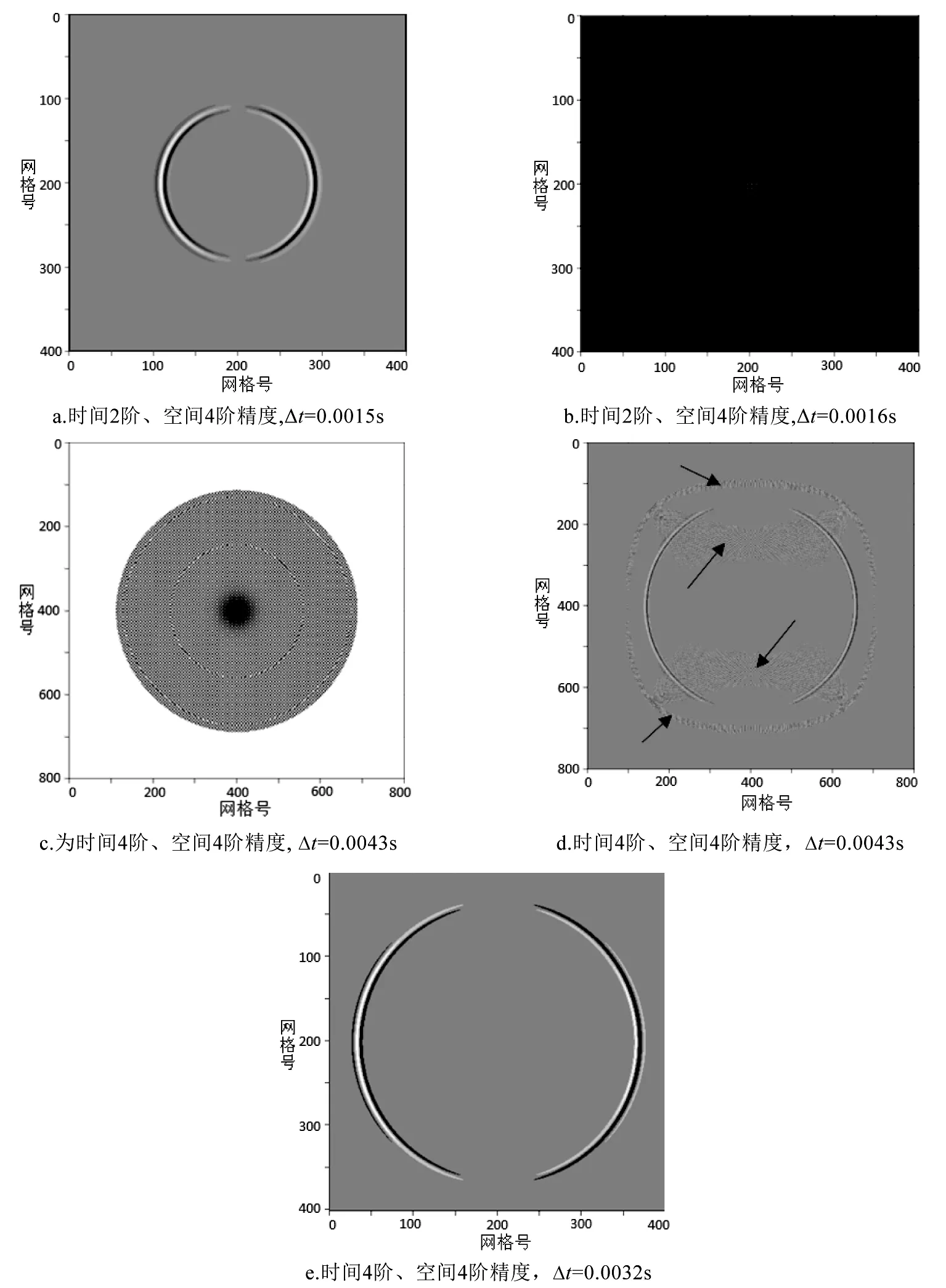
图1 不同差分阶数和时间步长的波场快照Figure 1 Wave field snapshot of different difference orders and time step lengths
数值解稳定且能准确描述波前。
仍然令f=30Hz,Δh=5m。选取时间4阶、空间4阶精度差分格式进行正演模拟。由表1可知,满足稳定性条件的最大时间步长为0.004 31s。
令Δt=0.004 4s,计算空间801×801个网格点,震源位置(401,401),记录第250个采样时刻,即1 100ms的波前快照,如图1(c),可以看到,当Δt>Δtmax时,数值解变得不稳定。当Δt=0.004 3s,记录第250个采样时刻,即1 075ms的波前快照。如图1(d),Δt=0.004 3s时,Δt<Δtmax,虽然波前得到了成像,但出现了许多不应有的“杂波”(箭头所指处)。这些“杂波”是由于时间步长过大所产生的由时间差分引起的频散。
仍然令f=30Hz,Δh=5m。选取4阶时间精度、4阶空间精度差分格式进行正演模拟。令Δt=0.003 2s,计算空间401×401个网格点,震源位置(201,201),记录t=230Δt,即736ms的波前快照,如图1(e)。
虽然为了避免数值频散,实际应用中时间步长不能取到稳定性条件条件允许的最大值。但是比起时间2阶、空间4阶精度差分格式稳定性条件允许的时间步长最大值Δtmax=0.001 5s,时间4阶、空间4阶精度的时间步长Δt已经可以取到其两倍以上。
4.2 提高时间差分精度对空间差分引起的数值频散的作用
以图1中的模型和初始条件为例,令子波主频f=60Hz,Δh=5m。选取2阶时间精度、4阶空间精度差分格式进行正演模拟。时间剖分步长为0.001 3s,计算空间401×401个网格点,震源位置(201,201),t=350Δt(455ms)的波前快照如图2a,在子波频率变高,波长变短,网格步长不变的情况下,一个波长内的节点数减少,因此由空间采样率不足造成了较为严重的频散。
将时间差分精度提高到4阶,其他条件不变,得到如图2b的正演结果。二者的比较表明,时间差分精度的提高并没有降低空间差分引起的数值频散。相反,由空间差分引起的数值频散变得更加严重。
保持时间差分精度为4阶,将空间差分精度提高至8阶,得到如图2c的正演结果。随着空间差分精度的提高,空间差分引起的数值频散显著降低。
从理论上看,由时间差分引起的数值频散是时间采样不足引起的,而空间差分数值频散是由空间采样不足引起的[17],因此数值频散需要根据频散的来源进行压制,不能通过提高时间(空间)差分精度来压制空间(时间)差分引起的频散。

图2 不同差分阶数条件下455ms时刻的波场快照Figure 2 Wave field snapshot at time 455ms underdifferent difference orders
5 结论与建议
本文在利用一阶速度-应力方程进行弹性波正演模拟的过程中,通过将速度(应力)对时间的导数转化为应力(速度)对空间的导数,使得高阶时间高阶导数的计算可以只通过一个时间层上的空间差分进行逼近,从而降低了计算所需的内存。同时,本文对Un+1/2=Un-1/2+A·Un类型的差分格式进行了稳定性分析,得到了一阶弹性波方程高阶时间差分格式相比一阶弹性波方程2阶时间差分格式的稳定性条件宽松的结论。
时间高阶差分格式允许在数值模拟过程中使用更大的时间步长,从而减少数值模拟所需的时间层数。但目前该格式存在时间层内计算量大的问题。由于不同阶数的时间导数可以用不同精度的空间差分进行逼近,因此在日后的研究中,可以利用不同精度的空间差分格式进行组合,进一步放宽稳定性条件的约束。
空间差分引起的数值频散是由空间上的网格离散造成的,而时间差分引起的数值频散是由时间上的网格离散造成的,两者来源不同。因此压制频散时要根据频散的来源进行压制,不能寄希望于通过提高一方的差分精度去压制另一方的频散。当时间步长过大时,由时间差分引起的数值频散会变得严重。

