额济纳旗盆地傍河潜水蒸发型稳定流解析解

边文英

(河北省地矿局国土资源勘查中心，石家庄 050000)

0 引言

全球有约三分之一的陆地位于干旱与半干旱地区，而且世界上近一半国家都在不同程度上受到干旱缺水问题的困扰。我国也不例外，尤其是西北地区干旱缺水问题更为突出，并且研究区蒸发十分强烈，降水稀少[1-4]。因此为了更好的研究在此条件下干旱区地下水的动态变化，本文在认真研究该区域水文地质条件特征的基础上，提出通过解析法计算傍河地下水在蒸发条件下典型剖面的潜水面分布情况，为研究此类地区水文地质条件提供了新思路。

本方法通过概化边界条件、建立数学模型，分别按照定水头和定流量两种补给方式，计算干旱区傍河地下水蒸发型一维稳定流潜水面的分布情况，此方法能够通过较少的参数，获取剖面地下水潜水面的分布情况，并且精度较高，对于具有相似水文地质条件地区可以直接利用本次计算成果，从而能够大大节省时间、减少工作量，为研究局部剖面地下水潜水面分布提供依据。

1 数学模型及其求解方法

本文以选择一个傍河地下水蒸发型稳定流典型剖面为例进行介绍，典型剖面图见图1。现根据剖面的具体情况采用解析法对傍河地下水蒸发型一维稳定流进行分析。

1.1 数学模型

根据研究区的含水层结构、地下水系统的划分以及当地典型的气候特征，确定研究区的数学模型为源汇项只包括潜水蒸发的一维稳定流的潜水模型。

模型的水流控制方程为：

(1)

图1 典型剖面图Figure 1 Typical section

模型的边界条件：

h(x=0)=h0

(2)

(3)

式中：h为潜水位(m)；x为水平坐标；t为时间(d)；K为x方向的渗透系数(m/d)；Eg为潜水面的蒸发量(m/d)；h0典型剖面所傍河的水位高程；L为地下水位稳定时典型剖面距离河道的距离。

傍河地下水蒸发型稳定流解析解的具体求解方法如下。

1.2 定水头补给潜水面分布

1.2.1 线性蒸发定水头补给潜水面分布

根据潜水蒸发公式的不同选择分为线性蒸发公式和非线性蒸发公式两种方式求其解析解。线性蒸发根据定水头补给的数学模型，通过整理变形的不同，又分为两种。下面首先介绍线性蒸发公式的第一种变形求解方法。

(1)线性蒸发公式第一种变形

线性蒸发公式：

(4)

式中Dmax为潜水蒸发为零时的地下水极限埋深，E0为水面蒸发强度，h为潜水含水层厚度，z为潜水含水层底板到地面的高度。

定水头补给-数学模型：

(5)

h(x=0)=h0

(6)

(7)

将(4)代入(5)：

(8)

(9)

(10)

设y=h2，则(8)转化成(11)

(11)

y″-By=A

(12)

方程(12)为二阶常系数非齐次线性微分方程，因此若想求(12)的通解，归结为求对应的齐次方程y″-By=0的通解和非齐次方程(12)本身的一个特解。

齐次方程y″-By=0的通解：

为常数)

(13)

非齐次方程(12)的特解：

(14)

则方程(12)的通解为：

(15)

即：

(16)

根据控制方程(6)、(7)可求得常数C1、C2的值：

(17)

(18)

将(17)和(18)值代入(16)，整理得(19)：

(19)

再将(9)和(10)代入(19)得最终定水头补给线性蒸发的潜水面形状方程:

(20)

根据所求出的定水头补给线性蒸发的潜水面形状方程，在理想状态下得到其潜水面形状，见图2。假设h0=50m，z=53m，k=20m/d，Dmax=5m，E0=0.005 479m/d，L=1 000m。

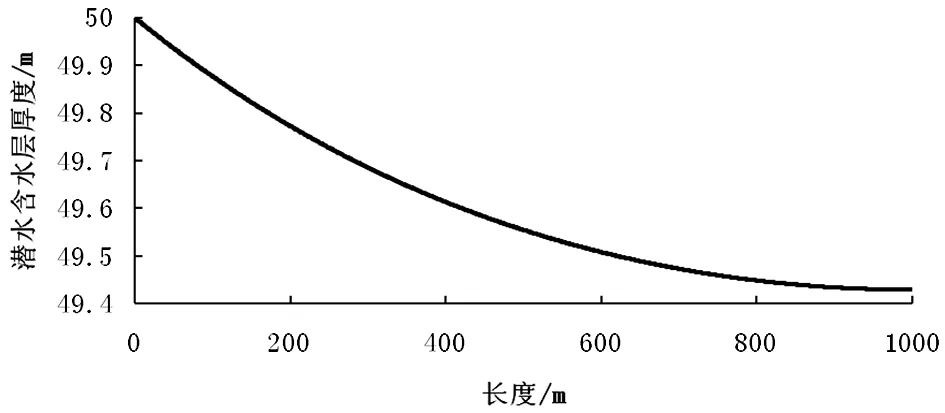
图2 定水头补给潜水面形状图Figure 2 Phreatic water table form under constantwater head recharge

(2) 线性蒸发公式第二种变形

线性蒸发公式：

(21)

定水头补给—数学模型：

(22)

h|x=0

(23)

(24)

将(21)代入(22)最终得(25)：

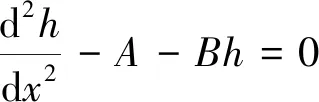
(25)

(26)

(27)

h″-Bh=A

(28)

方程(28)为二阶常系数非齐次线性微分方程，因此若想求它的通解，先求对应的齐次方程h″-Bh=0的通解和非齐次方程(28)本身的一个特解。

齐次方程h″-Bh=A的通解：

为常数)

(29)

非齐次方程(28)特解：

(30)

则方程(25)的通解为：

(31)

根据控制方程(23)、(24)得C1、C2的值：

(32)

(33)

将(32)和(33)代入(31)，整理得：

(34)

再将(26)和(27)代入(34)得最终定水头补给的线性蒸发的潜水面形状方程:

(35)

根据所求出的定水头补给线性蒸发的潜水面形状方程，在理想状态下得到其潜水面形状，见图3。假设h0=50m，z=53m，k=20m/d，Dmax=5m，E0=0.005 479m/d，L=1 000m。

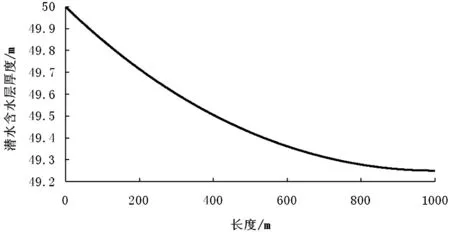
图3 定水头补给潜水面形状图Figure 3 Phreatic water table form under constantwater head recharge

1.2.2 非线性蒸发定水头补给潜水面分布

由于非线性蒸发的公式比较复杂，直接求其解析解存在一定难度，因此本文采用龙格-库塔方法(数学手册，2005)[5]。下面简单介绍龙格-库塔方法的计算公式和步骤。

(1)龙格-库塔方法

使用龙格-库塔方法计算，需要两个前提，即存在含多个未知函数的微分方程组：

(36)

(37)

初始条件：y(x0)=y0,z(x0)=z0

(38)

龙格-库塔方法具体计算公式:

(39)

其中：

先计算k1、k2、k3、k4、l1、l2、l3、l4，再计算yn+1和zn+1。

(2)非线性蒸发潜水蒸发面的求解

目前有关潜水蒸发的经验公式较多,比较典型的主要有:阿维里扬诺夫的潜水稳定蒸发抛物线型公式(1958),叶水庭等人(1977)提出的潜水蒸发指数型公式;随着研究的深入,无作物条件下计算潜水蒸发的阿维里扬诺夫公式、指数型公式已被用于有作物条件下潜水蒸发的计算,特别是阿维里扬诺夫经验公式的应用更为广泛。但是由于阿维里扬诺夫公式当大气蒸发力较大时会过高估计潜水蒸发量，而指数型公式可以弥补这一问题[6-12]。因此本次非线性潜水蒸发选取叶水庭公式(1977)，叶水庭公式如下：

Eg=E0e-αD=E0e-α(z-h)

(40)

式中，α为衰减系数，通过实测资料确定;D为潜水埋深,E0为水面蒸发，z为地面高程，h为潜水面高程。

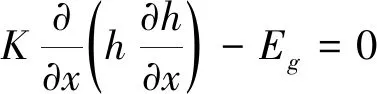
(41)

h(x=0)=h0

(42)

(43)

将(40)代入(41)得：

(44)

将(44)做无量纲化处理最终得(45)：

(45)

其中：xD=x/L,hD=h/h0,zD=z/h0

(46)

无量纲数学模型-定水头补给：

(47)

hD(xD=0)=1

(48)

(49)

将(47)分解为2个常微分方程，构成方程组

(50)

(51)

在excel表格中从xD=0开始计算,知道hD(0)和y(0)。先假设一个y(0)=C(常数)。计算一系列hD(x)和y(x)的数值，直到获得y(xD=1)=0，可能不等于零。调整y(0)的猜测值，直到y(x=1)=0或无限接近于0为止。计算结果见图4。

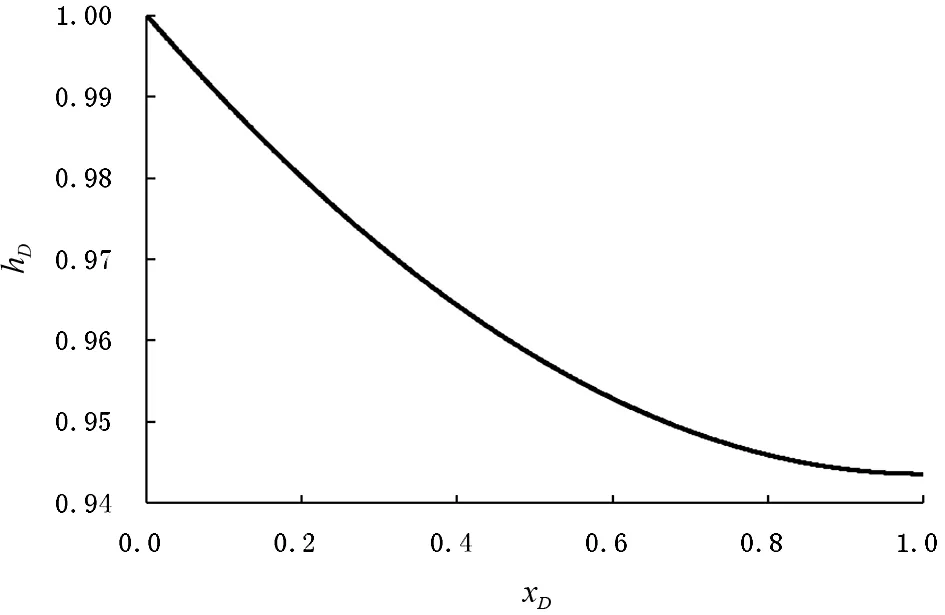
图4 定水头补给潜水面形状图Figure 4 Phreatic water table form under constantwater head recharge

1.3 定流量补给潜水面分布

定流量补给的潜水面分布的求解方法和定水头求解方法和步骤基本相同，只是数学模型发生变化。

1.3.1 线性蒸发定流量补给潜水面分布

(1)线性蒸发公式第一种变形

线性蒸发公式：

(52)

式中Dmax为潜水蒸发为零时的地下水极限埋深，E0为水面蒸发强度，h为潜水层厚度，z为潜水层地板到地面的高度。

定流量补给-数学模型：

(53)

(54)

(55)

所求方程和定水头求解方法一致，只是控制条件发生变化，即C1、C2变化，因此不再赘述。

即：

(56)

(57)

(58)

将(57)和(58)代入(56)中，整理得：

(59)

再将(9)和(10)代入(59)得最终定流量补给的线性蒸发的潜水面形状方程：

(60)

根据所求出的定流量补给线性蒸发的潜水面形状方程，在理想状态下得到其潜水面形状，见图5。假设h0=50m，z=53m，k=20m/d，Dmax=5m，E0=0.005 479m/d，L=1 000m，q=1.33m3/d。

图5 定流量补给潜水面形状图Figure 5 Phreatic water table form underconstant flow recharge

(2) 线性蒸发公式第二种变形

线性蒸发公式：

(61)

定流量补给—数学模型：

(62)

(63)

(64)

所求方程和定水头一致，只是控制条件发生变化，即C1、C2变化。

即：

(65)

(66)

(67)

将(66)和(67)值代入(65)，整理得：

(68)

再将(26)和(27)代入(68)得最终定流量补给的线性蒸发的潜水面形状方程:

(69)

根据所求出的定流量补给线性蒸发的潜水面形状方程，在理想状态下得到其潜水面形状，见图6。假设h0=50m，z=53m，k=20m/d，Dmax=5m，E0=0.005 479m/d，L=1 000m，q=1.63m3/d。

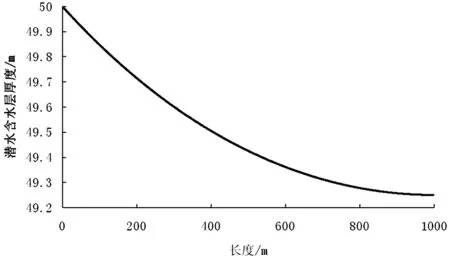
图6 定流量补给潜水面形状图Figure 6 Phreatic water table form under constant flow recharge

1.3.2 非线性蒸发定流量补给潜水面分布

叶水庭公式：

Eg=E0e-αD=E0e-α(z-h)

(70)

式中，α为衰减系数，通过实测资料确定;D为潜水埋深,E0为水面蒸发，z为地面高程，h为潜水面高程。

数学模型：

(71)

(72)

(73)

将(70)代入(71)得：

(74)

将(74)做无量纲化处理得(75)：

(75)

(76)

其中：xD=x/L,hD=h/z

无量纲数学模型-定流量补给：

(77)

(78)

(79)

将(77)分解为2个常微分方程，构成方程组

(80)

(81)

在excel表格中从xD=0开始计算,知道hD(0)和y(0)。先假设一个hD(0)=C(常数)，y(0)=-q/K。计算一系列hD(x)和y(x)的数值，直到获得y(xD=1)=0，可能不等于零。调整hD(0)的猜测值，直到y(xD=1)=0或无限接近于0为止。计算结果见图7。

图7 定流量补给潜水面形状图Figure 7 Phreatic water table form under constant flow recharge

2 结论

①通过对一维蒸发型稳定流进行分析和计算，得到了一维稳定流在线性蒸发条件下的定水头补给和定流量补给的解析解；

②通过龙格-库塔方法，在excel中实现了一维稳定流在非线性蒸发条件下的定水头补给和定流量补给的潜水面形态；并且在计算的过程中分别对定水头补给和定流量补给做了无量纲化处理，计算结果对傍河典型剖面具有一定适用性。