配置高强非预应力钢筋的预应力混凝土梁受弯试验研究

李 强，马燕丰

(1.唐山学院 土木工程学院，河北 唐山 063000；2.唐山市城市建筑工程总公司，河北 唐山 063000)

近些年，我国大力倡导和推进高强钢筋应用于建筑工程。早在2012年，住房和城乡建设部印发的《关于加快应用高强钢筋的指导意见》中明确提出，要积极推广并使用500 MPa螺纹钢筋，同时加强高强钢筋混凝土结构构件抗震性能的研究，将开展600 MPa及以上螺纹钢筋产品的研发列为重点工作[1]。HRB600钢筋是采用微合金化工艺的一种新型高强度、高性能钢筋，在有效提升混凝土结构的安全性、经济性和灵活性的同时，其结构在高应力状态下的性能也引起了学者们的关注[2-4]，从而为HRB600钢筋的工程应用提供了有力的理论依据和试验基础。笔者将对配置HRB600非预应力钢筋的预应力混凝土梁进行受弯试验。

1 试验概况

1.1 构件设计

本试验共设计了7根试验梁，试验梁的变量参数分别为非预应力钢筋强度、HRB600钢筋配筋率和混凝土强度等级。试验梁横截面均为矩形，截面尺寸为400 mm×500 mm。预应力筋为直线型布置，均采用有粘结后张法张拉[5]。试验梁的具体尺寸及配筋详见图1，试验梁的参数见表1，混凝土的实测材料性能指标见表2，非预应力钢筋实测材料性能见表3。

图1 试验梁尺寸及配筋

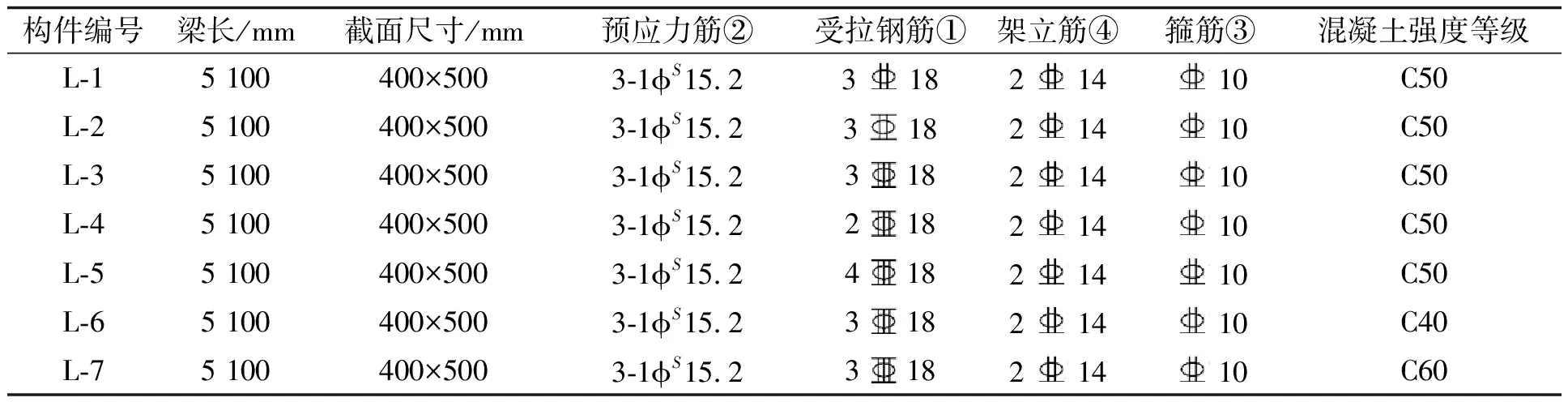
构件编号梁长/mm截面尺寸/mm预应力筋②受拉钢筋①架立筋④箍筋③混凝土强度等级L-15 100400×5003-1ϕS15.231821410C50L-25 100400×5003-1ϕS15.231821410C50L-35 100400×5003-1ϕS15.231821410C50L-45 100400×5003-1ϕS15.221821410C50L-55 100400×5003-1ϕS15.241821410C50L-65 100400×5003-1ϕS15.231821410C40L-75 100400×5003-1ϕS15.231821410C60

表2 混凝土实测材料性能 MPa

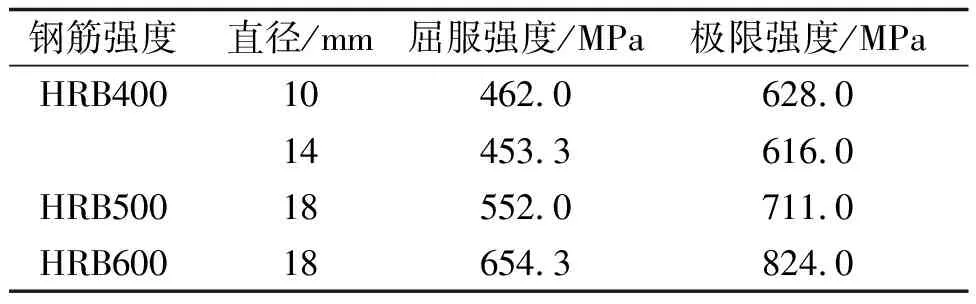
表3 非预应力钢筋实测材料性能

1.2 加载方案

本试验为静载试验，采用三分点对称加载，加载方案包括预加载和正式加载两个阶段。预加载每级加载20 kN，共加载两级；正式加载级距为20 kN，当总加载值接近特征荷载时，加载级距减半。当非预应力钢筋屈服后，加载方式改为位移控制，加载级距为1 mm，当非预应力钢筋应变达到约10 000 με或试验梁跨中挠度达到其跨度的1/50时，宣告试验梁破坏[1，6，7]。加载方式如图2所示。

图2 加载方式

2 试验结果分析

2.1 混凝土应变分析

本试验采用混凝土应变片采集试验梁跨中侧面混凝土应变情况，应变片粘贴位置见图2，跨中截面混凝土应变分布如图3所示。在试验梁受力过程的初始阶段，构件基本处于弹性阶段，混凝土应变沿构件截面高度方向呈直线型分布，故符合平截面假定。随着加载值增大，混凝土平均应变直线型分布虽有所折线化，但仍基本符合平截面假定。总体而言，配置HRB600非预应力钢筋的预应力混凝土梁的跨中截面平均应变近似线性分布，符合平截面假定[7]。

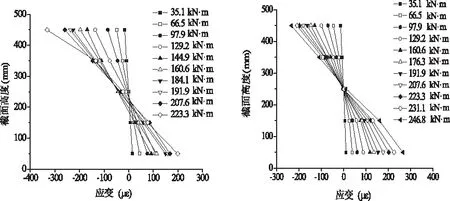
(a)L-4 (b)L-5

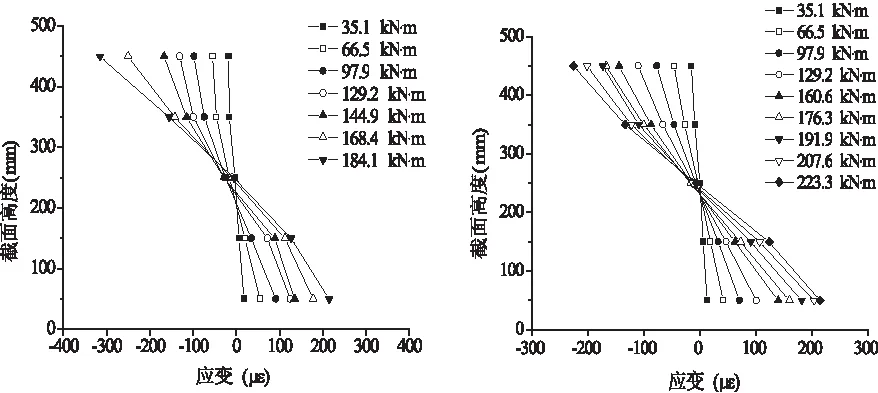
(c)L-6 (d)L-7图3 跨中截面混凝土应变分布

2.2 非预应力钢筋应变分析

本试验用应变片采集非预应力钢筋在加载过程中的应变情况，应变片的粘贴位置在受拉钢筋的跨中处。图4为试验梁荷载-非预应力钢筋应变曲线，将图4中(c)(d)与(a)(b)进行对比，不难发现HRB600钢筋与HRB500，HRB400的受力特征相似，钢筋应变发展均呈现出比较明显的三阶段增长规律：加载初期，钢筋发生弹性变形，其应变曲线近似直线型，且增幅较小；加载中期，尤其是试验梁开裂后，开裂处混凝土退出工作，非预应力钢筋拉应力大幅增加，应变曲线斜率减小；加载后期，钢筋在高应力状态下发生屈服，其应变的增速再次加快，应变曲线斜率再次减小，随着荷载进一步增加，试验梁的受弯承载力基本处于滞涨状态，而此时非预应力钢筋应变急剧增大，直至接近或达到10 000 με，宣告试验梁破坏。综观加载过程，HRB600钢筋的三阶段受力过程明显，在HRB600钢筋屈服后，其应变能够继续稳定增长，这表明HRB600钢筋的高强度和延性能够得到充分发挥，从而试验梁的受弯承载力得到了显著提升。

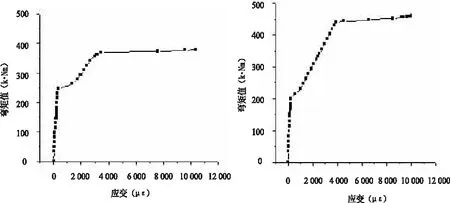
(a)L-1 (b)L-2

(c)L-4 (d)L-5图4 试验梁荷载-非预应力钢筋应变曲线

2.3 预应力损失分析

表4 预应力筋的有效预拉应力

3 挠度分析

3.1 短期挠度分析

影响高强钢筋混凝土梁短期挠度的三个基本因素包括荷载、初始刚度和配筋率[9]。本文考虑到非预应力钢筋和预应力筋的配筋率对试验梁短期挠度的显著影响，提出在现行《规范》短期抗弯刚度公式的基础上引入综合配筋率影响系数α(取值1.5)，从而对试验梁的短期跨中挠度计算值进行修正。

Bs=

(1)

表5 试验梁跨中挠度实测值与计算值对比

分析表5中的数据可知，试验梁短期跨中挠度的试验值与计算值的比值均值为0.971，变异系数为0.095；如果去掉偏差较大的试验梁L-5的试验数据再进行统计，比值为1.002，变异系数为0.057。由此可见，考虑到HRB600钢筋和预应力筋对试验梁抗弯刚度的提升作用，通过引入综合配筋率影响系数对《规范》中的公式进行修正，进而使计算值与试验值非常接近，可以提高短期跨中挠度的计算精度。

3.2 挠度限值分析

现行《规范》规定预应力混凝土受弯构件的长期最大挠度值要满足限值要求，试验梁的荷载长期作用下的截面抗弯刚度计算公式为：

(2)

式中Mk，Mq分别为按照荷载的标准组合、准永久组合计算的最大弯矩(kN·m)，本试验取Mk/Mq=1.143。

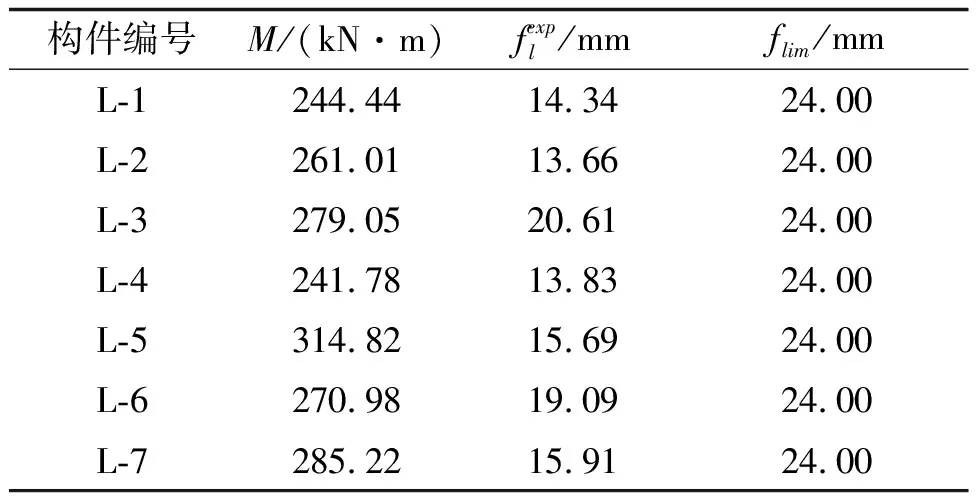
表6 试验梁挠度限值分析

注：试验梁的跨中挠度限值取flim=l0/200，即flim=24 mm

4 结论

本文通过对配置HRB600非预应力钢筋的预应力混凝土梁进行受弯试验，分析了混凝土和HRB600钢筋的应变发展规律，提出了预应力筋预应力损失的计算建议，研究了试验梁短期跨中挠度的计算方法，主要研究结论如下：

(1)试验梁跨中截面混凝土的平均应变近似呈线性分布，符合平截面假定。综观整个受力过程中，HRB600钢筋的荷载-应变曲线呈现出显著的三阶段增长规律，尤其在HRB600屈服后，其应变仍能够稳定增长，这表明HRB600钢筋与预应力筋协同受力较好，HRB600钢筋的高强度和延性得以充分发挥。

(2)预应力筋的各项预应力损失值宜按照现行《规范》公式进行计算，在计算预应力筋应力松弛损失值以及混凝土收缩和徐变引起的损失值时，通过引入时间影响系数，可以有效提高两类损失值的计算准确性。

(3)在计算配置HRB600非预应力钢筋的预应力混凝土梁的短期抗弯刚度时，要充分考虑HRB600钢筋和预应力筋配筋率对抗弯刚度的贡献，本文建议引入综合配筋率影响系数以提高计算精度，试验梁在正常使用极限荷载长期作用下的最大挠度符合限值要求。