基于变等效因子的PHEV等效燃油消耗最小策略*

刘晓真 ，付主木 ，2*

（1.河南科技大学信息工程学院，河南 洛阳 471023；2.河南省机器人与智能系统重点实验室，河南 洛阳 471023）

0 引言

混合动力汽车（Hybrid Electric Vehicle，HEV）在降低油耗和减少排放等方面发展潜力巨大，已成为当前研究的热点问题之一［1-2］。HEV有多个动力源，需要合理分配各动力源之间的功率，因此，开发合理有效的能量管理策略是极其重要的。目前对各动力源之间能量最优分配的研究主要是采用动态规划等方法实现全局最优化［3］，但其不足之处是行驶工况需要完全已知，不利于能量的实时最优分配，且对于电量维持型HEV，车辆行驶消耗的能量最终来源于发动机，而最优化问题的目标函数一般为发动机燃油消耗，没有将电机作为动力源对电能的消耗考虑在内，不能反映车辆真实的燃油经济性。对此，Paganelli G等［4］率先基于能量平衡提出了基于等效燃油消耗最小策略（Equivalent Consumption Minimization Strategy，ECMS）的瞬时优化控制策略，将发动机的油耗和电机所消耗电能的等效油耗归结为统一的能耗指标，用于解决能量的实时最优分配问题。目前该方法在HEV能量管理策略研究领域得到了普遍的认可［5-6］。

对于ECMS，等效因子是决定控制策略有效性的关键［7］。Sciarretta A 等［8］针对充电和放电两种情况设计了两个等效因子参量，并将参量纳入到等效燃油消耗的计算中，提高了计算精度。Musardo C等［9］根据过去和预测的车速以及由GPS收集到的未来短时间内工况数据，在线调整等效因子，获得良好的燃油经济性的同时，电池SOC也得到了很好的控制，并指出在给定的循环工况下，设计一个等效因子也能实现良好的燃油经济性。林歆悠等［10］利用遗传算法对特定工况下的等效因子进行了全局优化，但是该恒等效因子不能保证在其他工况最优的燃油经济性；Gurkaynak Y［11］等提出一种基于神经网络的工况识别器，根据过去一段时间内表征工况的特征参数来判断当前的工况类型，从而选取相对应的等效因子，减小了ECMS对工况的敏感性，但同时工况识别器的设计也增加了控制算法的复杂性。

基于此，本文针对一种并联式混合动力汽车（Parallel Hybrid Electric Vehicle，PHEV），设计了一种变等效因子的ECMS，以增强对工况的适应性。

1 PHEV动力总成结构及工作模式分析

1.1 PHEV动力总成结构

本文研究对象采用一个电机、两个离合器相结合的双轴并联式混合动力汽车结构，如图1所示。该结构相对简单，能量利用率较高，且应用较为广泛。

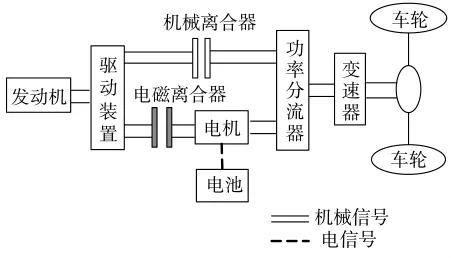
图1 PHEV动力总成结构

该结构中发动机通过驱动装置、电磁离合器与电机相连，通过控制电磁离合器的状态可实现发动机的快速起停。通过控制机械离合器的状态可以实现行车充电、发动机单独驱动、混合驱动、电机单独驱动多种工作模式。不同的工作模式之间，能量流动情况也不同，需要对其工作模式进行分析。

1.2 工作模式分析

根据功率守恒原则，发动机输出功率Pice、电机输出功率Pem、整车需求功率Preq之间的关系可表示为：

假设离合器闭合时不发生功率损耗，则PHEV在驱动状态下有如表1所示的4种工作模式。

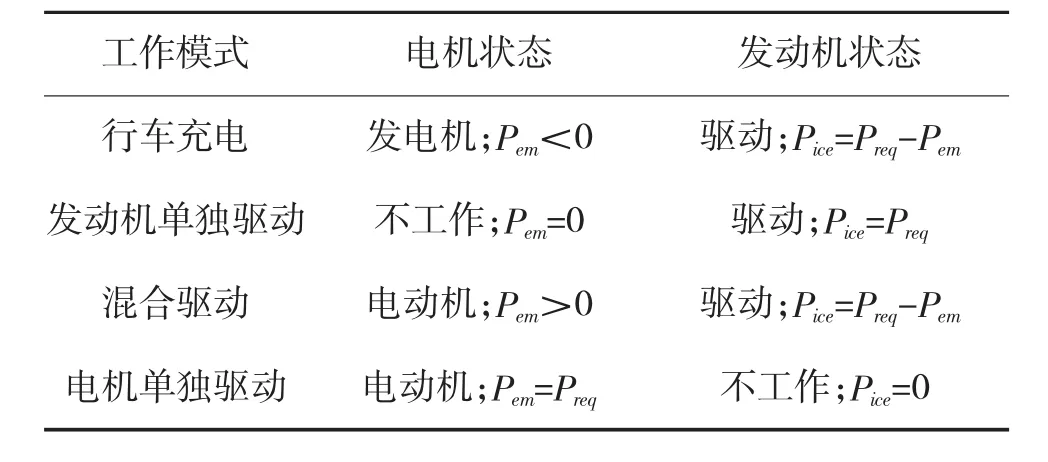
表1 PHEV的工作模式

不同的工作模式下，燃油的化学能和电池的电能都有不同程度的参与。车辆在整个行驶过程中，如果只考虑发动机的燃油消耗而不考虑电机对电能的消耗，则不能反映车辆真实的燃油经济性，因此，能量管理控制策略的设计需要将电机对电能的消耗一并考虑。

2 等效燃油消耗最小控制策略

对电量维持型HEV来说，车辆在行驶过程中消耗的所有能量最终均来源于燃油。电池只是调节发动机输出功率的能量缓冲器，在某一控制周期，车辆行驶中消耗的电池电能，需要在未来的时间消耗一定量的燃油进行补充，从而达到整个行驶周期结束后电池的SOC保持不变。因此，需要建立消耗电池电能与主动补偿电能所需消耗的燃油之间的等效关系，将发动机瞬时燃油消耗与消耗电能所等效的燃油消耗量归结为统一的能耗指标，为优化控制奠定基础。

结合等效燃油消耗思想，可以确定任一时刻下以整车等效燃油消耗率为优化控制的目标函数，目标函数可以写为

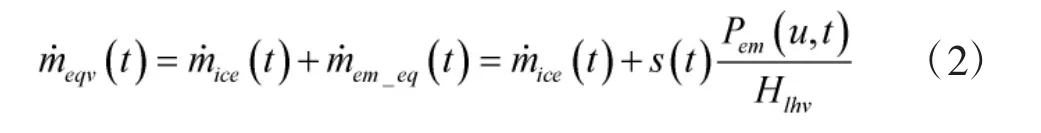
系统需满足以下约束条件

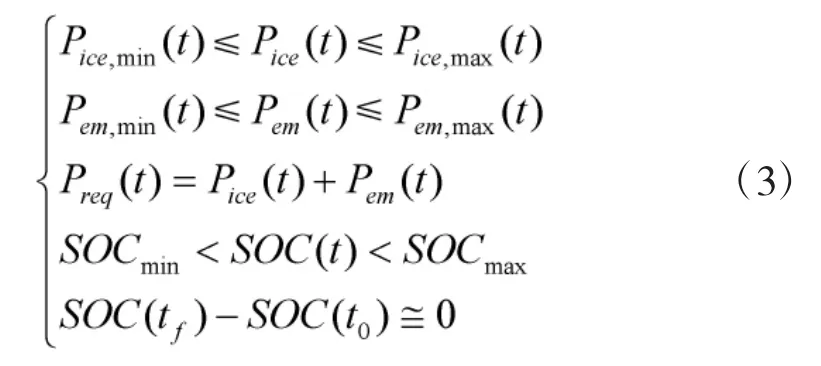
选定电机输出功率Pem为控制变量。在目标函数的约束条件下，以整车等效燃油消耗率最小为控制目标，结合发动机高效运行MAP图，计算得出控制目标最小时所对应的整车等效燃油消耗最小值和控制变量的值。进而确定发动机和电机的瞬时最优功率分配以及对应的工作模式。

对式（2）的求解，可引入庞特里亚金极值原理（Pontryagin′s Minimum Principle，PMP），构建哈密顿函数

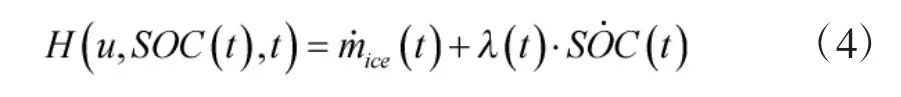
式中，λ（t）为协状态变量；SO˙C（t）为电池 SOC 动态方程。电池SO˙C的动态方程为

式中，Ib为电池电流，C为电池容量。电池电流为

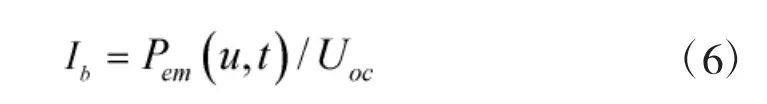
式中，Uoc为电池开路电压。

结合式（2）、式（4）～ 式（6）可得：

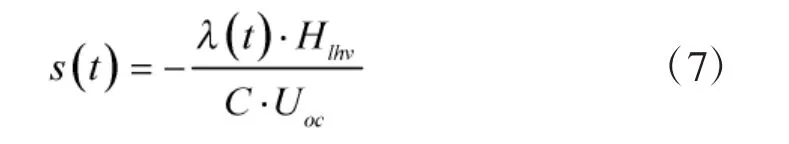
由式（7）可知，等效因子可以根据协状态变量λ（t）计算得出。如果行驶工况完全已知，则可以获得最优的协状态变量λ（t），从而获得最优的等效因子。

相关文献已经对Advisor中的每一种已知的行驶工况进行了离线计算，从而获得对应的最优等效因子［12-13］。本文将NEDC工况下对应的最优等效因子和UDDS工况下对应的最优等效因子均应用到UDDS工况进行仿真，得到如图2所示的SOC变化曲线。

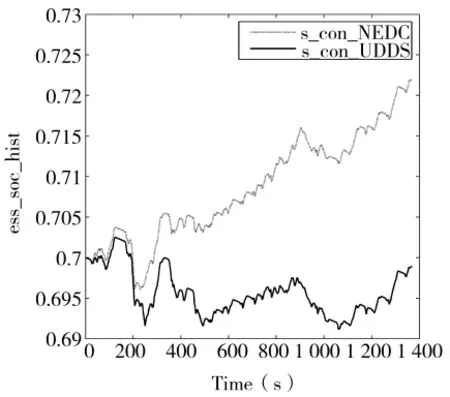
图2 不同等效因子在UDDS下的SOC变化曲线

分析图2发现，等效因子对工况的变化极其敏感，一种工况下恒定的最优等效因子在其他工况下很难保证最佳的燃油经济性。而车辆在实际运行中不一定能按预设的工况行驶，若实际工况与预设工况相差太大，就会导致等效燃油消耗计算误差太大，电池过充或过放的情况发生，不能保证整车的最佳燃油经济性。所以为了提高对行驶工况的适应性，有必要设计一个与实时工况相关的变等效因子。

3 变等效因子的设计

为了获得与实时工况相关的变等效因子，本文将引入SOC惩罚函数的概念，重新设计目标函数，获得等效因子的参考值，通过电池SOC惩罚函数和对参考值的修正在线调整获得一个与实时工况相关的变等效因子。

3.1 等效因子参考值的确定

由于车辆在实际运行过程中，行驶工况未知，只能使用局部历史信息进行估计，这将不可避免地产生与最优值的误差。PAGANELLI等［14］针对该问题提出了惩罚函数的概念，用于对电池电量的等效油耗进行修正，调节对电能的使用倾向，维持SOC在合理范围内。受该思想启发，可以重新定义一个包含对电池SOC的惩罚函数在内的整车等效燃油消耗目标函数

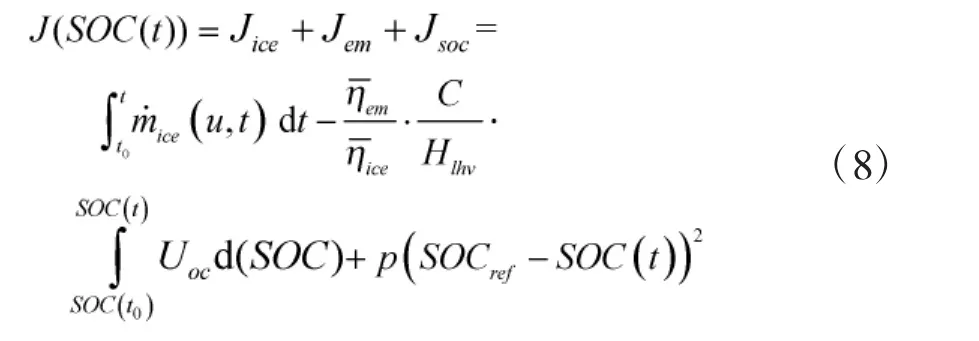
根据哈密顿-雅克比方程可得，最优协态变量为

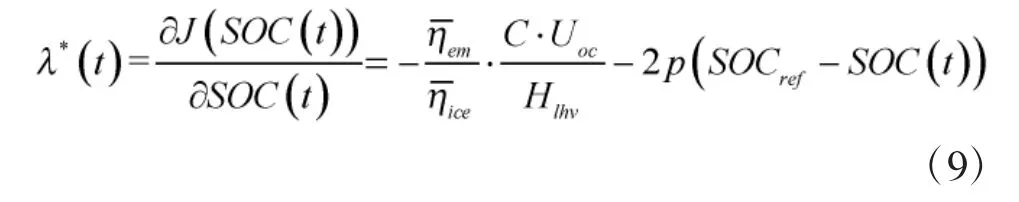
结合式（7）、式（9）可得

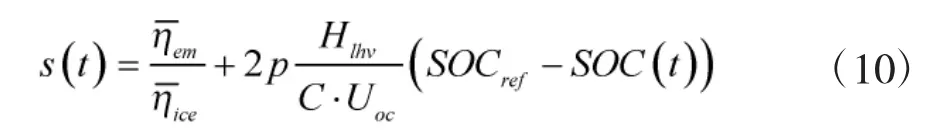
因此，定义等效因子的参考值为

3.2 惩罚函数的选取

由式（10）可知，在实时行驶工况下，根据电池SOC的惩罚函数，可以对等效因子进行在线的自适应调整，因此，惩罚函数的选取也很重要，有采用S拟合曲线的，有采用分段函数处理的，本文选取正切函数进行处理。

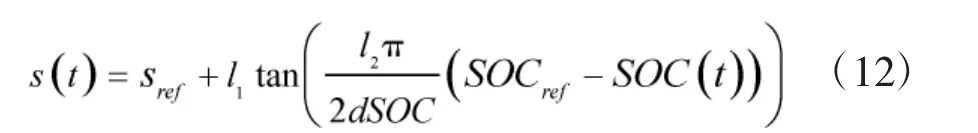
式中，sref为等效因子的参考值，此值可以根据上面的计算得到；dSOC为电池SOC允许的变化范围，l1、l2为调整参数，通过调整这两个值，可以控制惩罚函数的形状，进而控制惩罚函数对电池SOC变化的响应速度。

采用正切函数的电池SOC惩罚函数，可以快速地对SOC变化作出响应，有效地将SOC控制在一个合理的范围内，同时也提高了等效因子对工况的适应性。

3.3 变等效因子的确定

由式（12）可知，根据电池SOC的实时反馈，可在线调整等效因子，获得一个与实时工况相关的变等效因子。有研究表明，若使等效因子参考值随着等效因子的变化而变化，则能更大程度地降低等效因子初值的选取带来的整车燃油经济性问题［15］。

本文采用加权移动平均法，对等效因子的参考值进行调整，以使变等效因子对工况更具适应性。

调整规则为

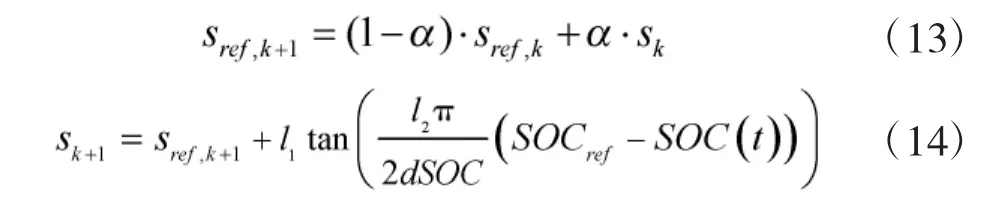
等效因子s（t）、电池SOC与实际工况密切相关，因此，采用该方法获得的变等效因子将能更好地适应复杂多变的行驶工况。

4 仿真及对比分析

为验证本文所制定的PHEV基于变等效因子的等效燃油消耗策略（Equivalent Consumption Minimization Strategy based on a Variable equivalent factor，V-ECMS）的合理性和有效性，对所设计的V-ECMS仿真与基于恒等效因子的等效燃油消耗策略（Equivalent Consumption Minimization Strategy based on a Constant equivalent factor，C-ECMS） 进行对比分析。

4.1 仿真参数选取

PHEV结构部件的主要参数如表2所示。

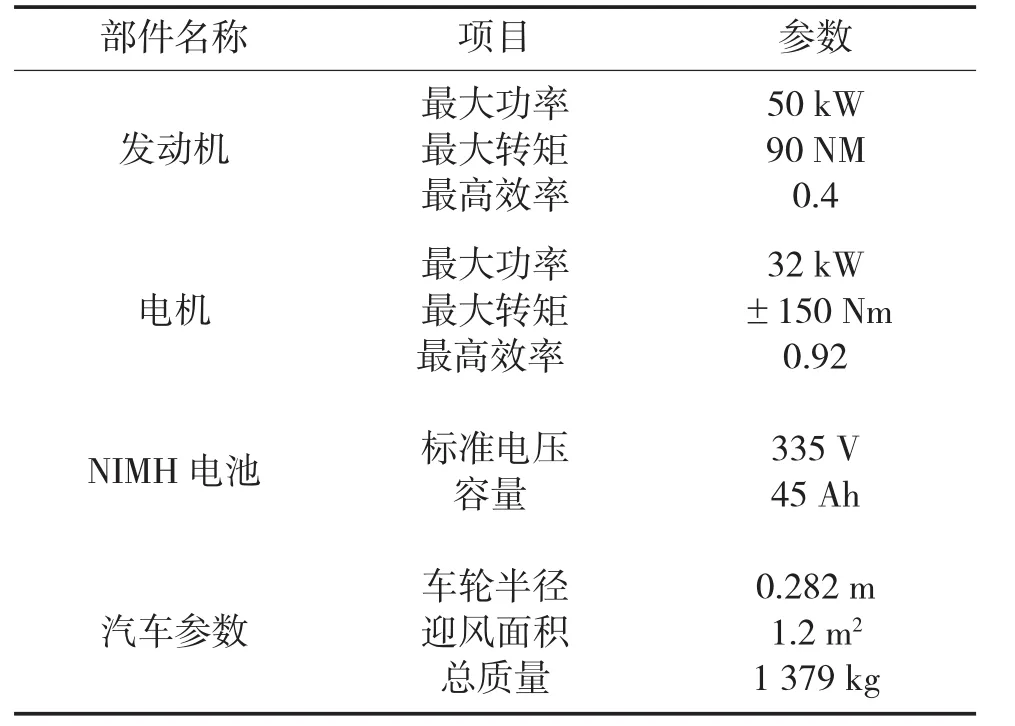
表2 整车主要部件参数

4.2 仿真及对比分析

为验证本文所设计的V-ECMS的合理性，仿真运行工况采用美国城市循环工况CYC_UDDS。仿真结果如图3和下页图4所示。

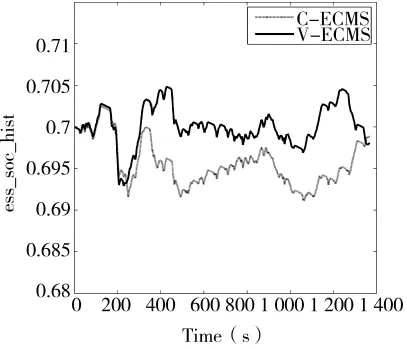
图3 不同控制策略在UDDS下的SOC变化曲线

图3为C-ECMS和V-ECMS在UDDS工况下的SOC变化曲线，对比发现V-ECMS和C-ECMS一样能够使电池SOC很好地维持在合理范围。图4为两种控制策略下的发动机工作点分布图，图4（a）和图4（b）比较可以看出，C-ECMS作用下的发动机运行点相对分散不集中；而V-ECMS作用下，发动机运行点大部分在高效区内且接近最优曲线，发动机运行效率整体得到提高。

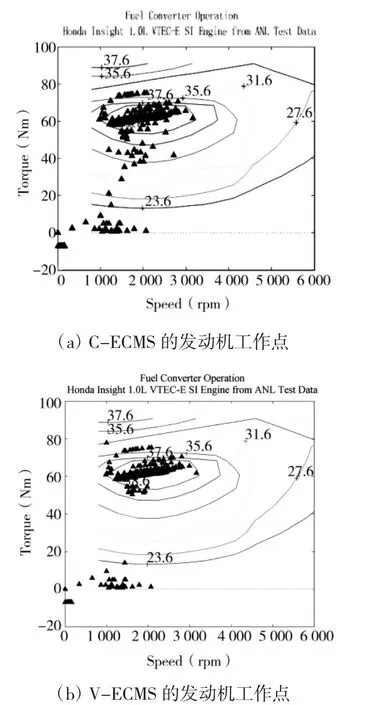
图4 发动机工作点分布图

仿真结果数据的对比如表3所示。由表3可以看出在V-ECMS作用下，发动机效率有所提高，百公里油耗明显降低，燃油经济性得到了明显改善。

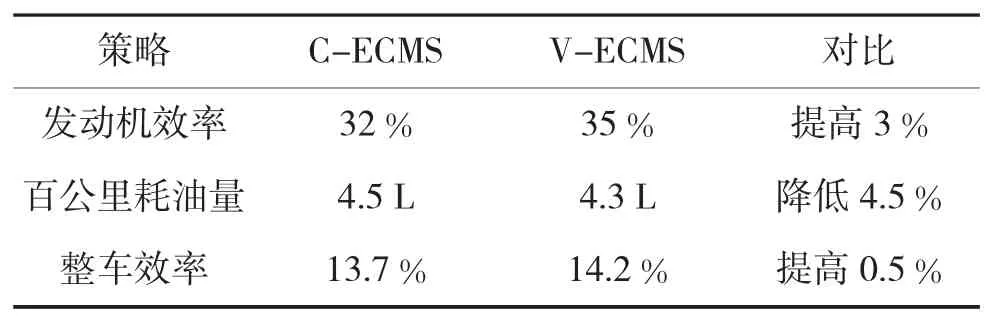
表3 仿真结果数据对比

为验证V-ECMS对复杂工况的适应性，行驶工况采用UDDS、NEDC、FTP 3种工况叠加的复合工况CYC_2，并与C-ECMS对应的仿真结果进行对比。行驶工况如图5所示。

复合工况下电池SOC变化曲线如图6所示。从图6可以看出，经过近10 000 s复杂多变的行驶工况的仿真，采用V-ECMS后，SOC终值接近于初始值，而采用C-ECMS后，SOC变化曲线呈现阶梯状下降趋势，电池损耗较大，不利于电池的长期使用，由此可以证明，V-ECMS对复杂多变的行驶工况有更高的适应性。

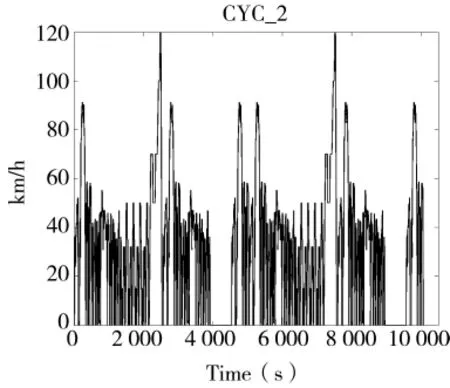
图5 复合工况

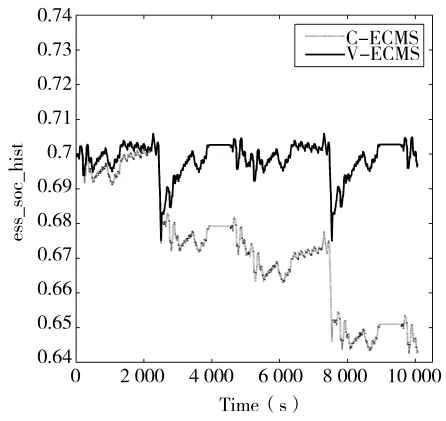
图6 复合工况下SOC变化曲线

5 结论

1）基于庞特里亚金极值原理，在行驶工况已知前提下，设计了一种C-ECMS。

2）提出了一种行驶工况未知时，变等效因子的确定方法，设计了一种V-ECMS，提高了整车等效燃油消耗量的计算精度和对行驶工况的适应性。

3）仿真和对比分析结果表明，所设计的V-ECMS能够使发动机运行点大部分集中在最优曲线上，电池SOC波动较小，与C-ECMS相比，发动机效率提高3%，整车系统效率提高0.5 %，百公里耗油量降低4.5 %。