无迹卡尔曼滤波的长码直扩信号载波频偏盲估计*

马 超，张立民

（海军航空大学信息融合研究所，山东 烟台 264001）

0 引言

直接序列扩频（DSSS）技术因其低截获能力、较强的保密能力和抗干扰能力，广泛应用于军事和民用通信领域。在实际应用中，收发双方的载波频偏严重影响系统性能。频偏估计是一个非线性问题，当接收端信噪比低于某门限时，估计性能迅速恶化，无法满足接收机解调的要求。关于载波频的盲偏估计成为了非协作通信领域研究的热点问题。为此，针对军事无线通信、卫星通信以及深空通信等接收端信噪比往往很低的通信系统，研究低信噪比条件下的载波频偏估计问题具有十分重要的意义。

常用的DSSS信号载频估计的方法较多，文献［1］提出了基于连续导频符号的最大似然（maximum-likelihood，ML）载波频偏估计方法，该方法将导频信号功率谱的全局最大值对应的频率作为频偏的估计值。基于连续导频符号的M L频偏估计具有较低的信噪比门限［2-3］，但估计精度有待进一步提高。适合用于长周期DSSS信号检测的方法主要有:能量检测法、相关累积法、平方滤波法、高阶累积量法等［4-8］。传统的能量检测法主要是通过利用信号加噪声能量大于噪声能量这一思想，不能充分利用信号特征信息，效果较差。相关累积法的主要思想是对信号作相关处理，优点是能够在低至-12 dB的条件下实现载频估计，但是需要较长的时间用来消除噪声，不适合实际应用。平方滤波法可以检测出信号的载频，但是在低信噪比条件下，其检测性能急速下降。

针对周期长码DSSS通信中的载波同步问题，提出了一种新的载波频偏估计算法。该方法结合分段和UKF算法的思想，利用UKF算法对非线性模型的求解能力，估计载波频偏的后验概率的均值和方差。

1 信号模型

持续时间为N个扩频周期的接收信号为

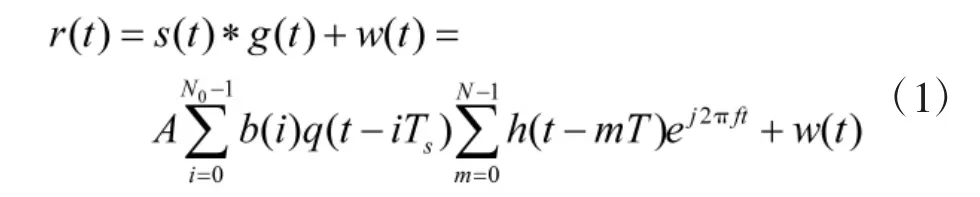
式中，s（t）表示持续时间为N个扩频周期的发射信号，f为载波频率，N0为N个扩频周期长度包含的信息符号的数目，g（t）表示信道回旋，*为卷积运算，通过载波同步［9］估计出信号载频，对接收信号r（t）进行下变频，并考虑载波频偏的影响，得到等效基带信号为

将式（3）以扩频周期进行分段，如图1所示。

则得到第n个分段信号表示为

图1 观测数据的分段示意图

研究目标就是在知道每一段数据R（n）的前提下，对参数空间进行估计。分析参数空间Θ中的元素可以发现，对于Δf参数，可以采用UKF方法进行估计。下面给出单用户时UKF算法的实现过程。

2 算法原理

无迹卡尔曼滤波［10］是一种递归式贝叶斯估计方法，但是不需要进行非线性模型的求解（即不需要求解雅可比矩阵），其基本思想［11］是利用UT（Unscented Transformation）转换，用一组确定的样本点近似求解测量条件下系统状态的后验概率密度的均值和方差，实现系统状态递推均值和方差（一、二阶矩）的估计［11］。

由第1节的信号模型可知，载波频偏的状态空间模型和观测方程分别为

1）参数的先验假设

先验分布的选取一般是基于两个原则:第一是简化计算；第二是对后验分布的影响最小（也就是无信息先验分布），在简化计算上，一般采用共轭先验分布，它能保证参数的后验分布与先验分布相同［12-13］。

由贝叶斯公式可知，参数空间的后验分布函数等价为

式中:p（R（n）|Θ）为似然函数，p（Θ）为联合先验概率密度函数。根据式（6）可得

由于噪声方差σ2的先验分布可认为服从逆伽玛分布（inverse Gama distribution）Ig（υ0，γ0），于是概率密度函数表达式为

本文选取υ0=γ0=0，逆伽玛分布就成了Jeffrey无信息先验分布

信息序列向量b（n）中的元素相互独立，可认为服从离散有限字符集上的均匀分布，若采用BPSK调制，则［12］。文中假设调制样式已知，所以离散有限字符集的数目已知，则其概率密度函数为

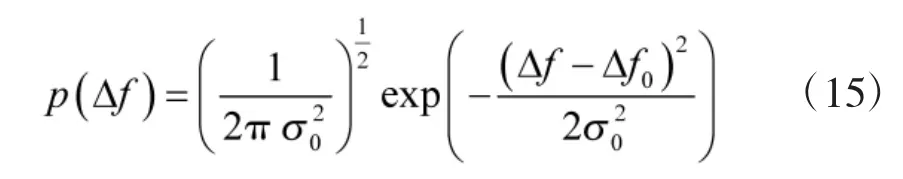
根据上述先验分布，式（11）可写成

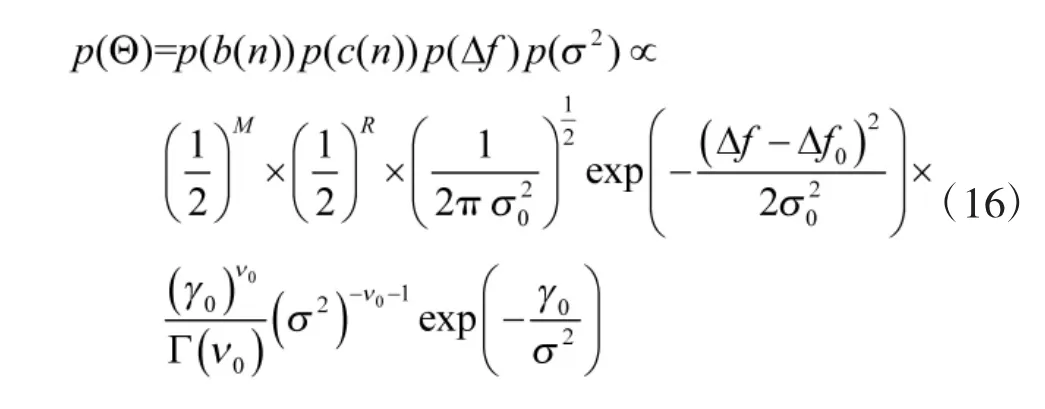
于是可得

于是结合式（10）并对σ2积分可得

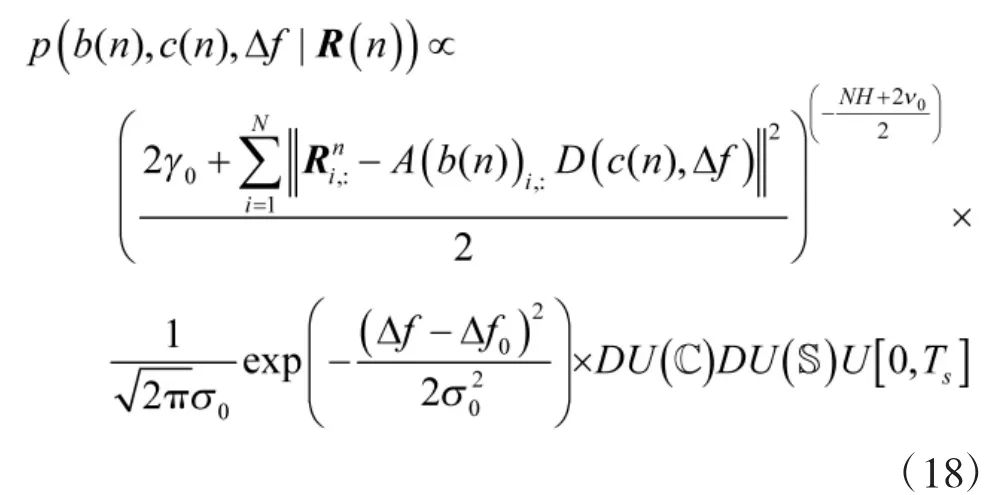
下面给出Δf的全条件后验分布。

根据式（7）和式（8）可知，在第n个观测周期，Δf服从高斯分布，即

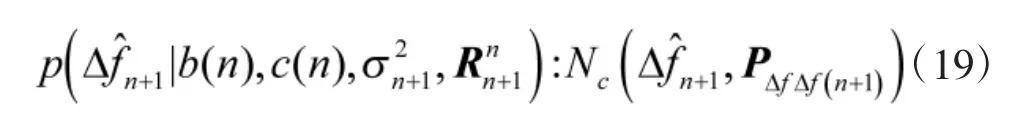
根据UKF算法，确定第n个周期的样本点Sigma集合及相应的权值

3 仿真实验与分析

本文算法是在长码直扩信号条件下推导出的，但由分段模型和推导过程可知，该算法对短码的直扩信号同样适应。算法进行500次迭代运算，由于算法收敛需要一个过程，为了增加仿真结果的可信度和准确性，因而取后400次的迭代结果进行相应的运算。

仿真条件:扩频码为R=63位随机序列，调制样式为BPSK，码片速率为10MHz，符号速率为10MHz/30=333.3 kHz，扩频增益P=30，仿真数据为N=300个扩频周期，分段长度H为8，重叠长度H0=H-1，则每个扩频周期分为S=56个片段。

图2给出了SNR=-9 dB时，采用后400次迭代值进行的载波频偏Δf的估计，并以直方图的形式表示，图2中横坐标的单位为码片速率fc，该图表明具有最大后验概率值的载波频偏非常接近真实值。仿真时Δf的真值为{0.1fc}。

图2 载波频偏后验分布直方图

4 结论

本文针对长码直扩信号的载波频偏盲估计问题，结合分段和UKF算法的思想，提出了基于分段的UKF的载波频偏盲估计算法。该算法结合分段的思想，利用UKF算法对非线性模型的求解能力，估计载波频偏的后验概率的均值和方差。该算法能够实现对短码和长码信号的有效估计，并且不受扩频序列类型的限制。仿真实验结果表明，该算法具有较好的低信噪比适应能力，且能获得较好的估计性能。本文仅研究了单用户情况下，对于多用户情况尚需进一步研究。