亚纯函数系数微分方程解的复振荡性质
王腾毅
亚纯函数系数微分方程解的复振荡性质
王腾毅
(贵州财经大学数学与统计学院,贵州,贵阳 550025)
综合运用Nevanlinna值分布的理论,Wiman-Valiron的理论及其它复分析中的常用方法研究了复域上高阶微分方程解带有小函数时复振荡的性质,该文的结果将二阶情形推广到高阶情形。
亚纯函数;微分方程;小函数
1 引言与主要结果
1.1 Nevanlinna值分布理论,Wiman-Valiron的理论简介

Wiman-Valiron的理论是研究考虑整函数系数微分方程的整函数解性质的一个十分重要的工具。


Picard定理:是复平面上的解析函数,并且始终不取值0,1,那么一定是一个常数。
1.2 亚纯函数系数微分方程解的复振荡性质领域的研究现状
目前主要研究的是二阶复域微分方程,对于高阶的情况,讨论较少。
2006年陈玉研究了二阶复域微分方程亚纯解的不动点与超级,得到了如下结论:






本文研究了一类高阶微分方程的亚纯解与其小函数的关系得到了如下结论。

和

至多有一个例外解,其他所有非零解都有无穷多个不动点,且满足
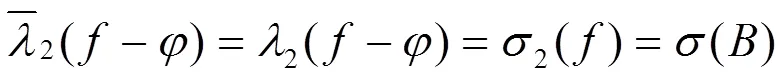

2 定理证明所需引理


和

则有



即


和
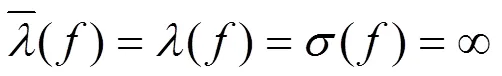





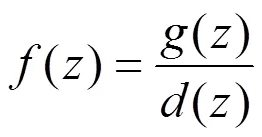


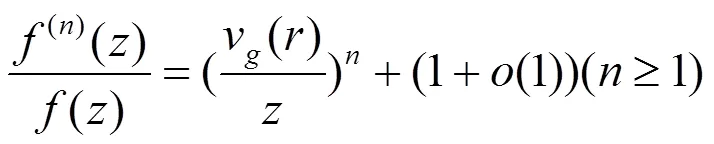


3 定理的证明

把(5)式代入(1)式并整理后得到


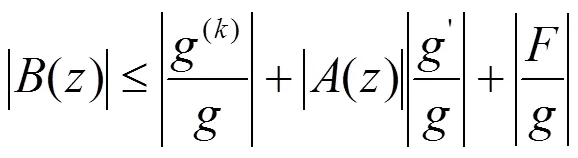


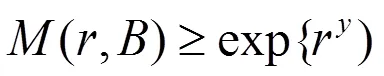



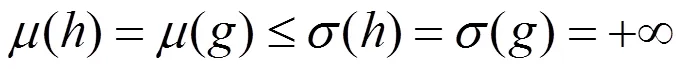

把方程(7)式改写为

把(14)式代入(15)式有

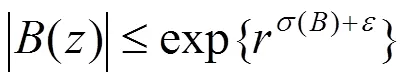

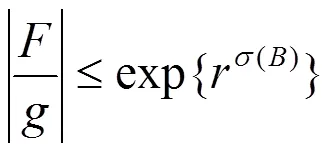
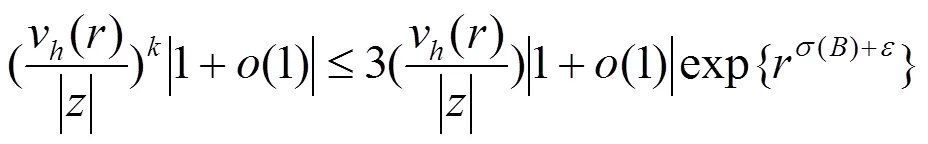




由式(22)及(23)可知

综上所述

4 总结
本文主要综合地运用了Nevanlinna值分布的理论,Wiman-Valiron的理论和其它复分析方法研究复数域高阶微分方程的解带有小函数时复振荡的性质,将二阶的情形推广到高阶情形中一种特殊情况,带有小函数应用的情况,得出了高阶情形下定理,并证明结论也成立。
[1] 陈玉,陈宗煊. 二阶复数域微分方程亚纯函数解的不动点与超级[J].大学数学,2006,22(6):78-81.
[2] 易才凤,边年英. 二阶微分方程亚纯函数解的零点收敛指数和增长级[J].江西师范大学学报:自然科学版,1998,22(1):16-20.
[3] 甘会林,易才凤. 高阶微分方程亚纯函数解的零点收敛指数和增长级[J].江西师范大学学报:自然科学版,2003,27(1):39-41.
[4] Gundersen G. Estimates for the logarithmic derivative of a meromorphic function ,plus similar estimates [J].J London Math Soc,1988,37(2):83-104.
[5] Chen Z X. The growth of solutions of second order linear differential equations with meromorphic coefficients [J].Kodai Math J,1999,22(1):208-221.
[6] 陈鸿辉,蔡金华,袁文俊. 涉及零点与多项式的无零点亚纯函数族的正规性[J].西南师范大学学报:自然科学版;2018,43(8):10-17.
[7] 刘志学,曹廷彬. 多复空间中亚纯函数在分担小函数情形下的唯一性结果[J].南昌大学学报:理科版;2016, 40(1):1-7.
The complex oscillation properties of the solutionsof differential equations with meromorphic coefficient
WANG Teng-yi
(School of mathematics and statistics, Guizhou University of Finance and Economics, Guiyang, Guizhou 550025, China)
In this paper, we mainly use the Nevanlinna value distribution theory, complex oscillation properties of Wiman-Valiron theory and other complex analysis method to study the characteristics of higher order ordinary differential equation with a small function in complex domain.The results of this paper extend the second-order case to the higher-order case.
meromorphic function differential equation small function
1674-8085(2019)03-0014-05
O174.52
A
10.3969/j.issn.1674-8085.2019.03.003
2019-01-18;
2019-04-03
王腾毅(1987-),男,安徽安庆人,助教,硕士,主要从事基础数学研究(E-mail:wangtengyi7009@163.com).

