热作模具热疲劳寿命评估及预测方法的研究进展
苏 楠 陈明和
南京航空航天大学机电学院,南京,210016
0 引言
随着科学技术和工业进程的飞速发展,高强材料的应用越来越广泛,对应用于高强材料成形的热作模具的需求和要求也越来越高[1]。在服役过程中,热作模具(如热锻模、热冲压模、压铸模和热挤压模等)在高温、高压、高应力等恶劣工作条件下受到热循环和载荷循环的共同作用,从而产生热疲劳裂纹直至破坏失效[2]。热作模具的热疲劳寿命直接影响热作模具的服役寿命,研究其热疲劳寿命评估及预测方法对模具工业的发展具有重要的工程和经济意义。
热疲劳研究的历史可追溯到1838年,Duhamel研究发现,物体在不均匀加热时会产生热应力,直至1976年,SPERA等[3]才对热疲劳研究做出了详尽的基础解释和分类,将其主要分为热应力疲劳与热机械疲劳两个研究方向。20世纪50年代Manson-Coffin公式[4-5](以下简称“M-C公式”)被提出后,热疲劳研究得到了从定性分析到定量研究的质的飞跃。国内外研究方向从简单的破坏分析逐渐过渡到裂纹萌生、扩展过程的研究,通常通过试验测量材料的热疲劳损伤因子,并利用数学模型表征应力应变-寿命关系,构建寿命预测模型来估算材料或构件的寿命。近年来,国内相关研究因热作模具的需求而得到了发展,钢铁研究总院、哈尔滨工业大学、上海大学、华中科技大学和吉林大学等对热作模具热疲劳的研究做了较多工作。
在高温合金材料热疲劳寿命研究的带动下,热作模具的热疲劳寿命评估及预测方法研究取得了一定的进展。虽然近20年国内外研究热度不减,但热作模具热疲劳涉及温度、蠕变、外加应力和高温氧化等复杂因素,以及试验与实际应用存在差距,因此热疲劳寿命的研究一直是热作模具寿命研究中极为复杂的问题。本文结合国内外现有研究成果,从热应力疲劳和热机械疲劳两方面介绍和评价了热作模具的热疲劳寿命评估及预测方法,并对热作模具热疲劳寿命预测的发展趋势进行了展望。
1 热疲劳寿命
材料在高温服役过程中,由温度交变作用引起的损伤或破坏现象称为热疲劳。通常将材料内部约束条件(材料自身热胀冷缩引起的内应力约束)下的热疲劳称为热应力疲劳(thermal-stress fatigue,TSF),将外部约束条件(外部阻止材料热胀冷缩体积变化或对材料施加载荷形成的约束)下的热疲劳称为热机械疲劳(thermal-mechanical fatigue,TMF)[6]。根据SPERA等[3]的解释分类(图1),热疲劳是低周疲劳过程中伴随循环温度变化的特殊情况。热疲劳区别于等温疲劳,但又受益于等温疲劳的研究而得到迅速发展。自1944年BOAS等[7]第一次提出热疲劳的概念以来,人们一直致力于热疲劳损伤行为和失效机理的研究,并通过调整材料的化学成分、改进制造工艺和零件结构等方法,来改善材料微观组织和受力状态、提高力学性能、减缓和阻止疲劳裂纹的萌生与扩展,以延长零件的使用寿命[8-9]。热作模具的使用环境决定了模具材料的选用,以及服役时必须考虑抗热应力疲劳和抗热机械疲劳的能力,使之获得更长的使用寿命(即产生更高的经济效益)。热疲劳寿命评估及预测方法正向可以指导模具材料性能测试或直接指导模具选材,逆向可以辅助模具材料有根据地进行寿命改良。
热作模具热疲劳寿命是指材料从服役开始到发生热疲劳失效之间的时间长度,失效标准从衡量对象角度通常分为如下3种形式:①能量的标准,当材料的累积承受能量超过既定能量容限时,材料失效;②应变的标准,当材料累积塑性变形达到一定程度时,材料失效;③宏观的标准,当萌生的裂纹达到一定长度或表面裂纹破坏达到一定面积时,材料失效。从失效的时间进程角度也可将热作模具热疲劳裂纹分为裂纹萌生、裂纹扩展和断裂3个阶段,由于前2个阶段是模具的有效使用寿命,因此热作模具的热疲劳寿命就是前2个阶段时间的总长度。
在热作模具热疲劳寿命研究中,热应力疲劳只是由单纯的温度变化而导致的热应变行为,而热机械疲劳更能贴合热作模具实际的服役工况,更能为热作模具热疲劳寿命的研究提供可靠的理论支持。但热应力疲劳能准确地研究单变量温度对材料热疲劳寿命的影响,是研究热机械疲劳寿命的重要基础,热应力疲劳的研究成果部分可延伸用于热作模具热疲劳寿命的评估与预测。由此可知,热作模具热疲劳寿命的评估与预测可总结为热应力疲劳研究和热机械疲劳研究两大类。
2 热应力疲劳
近年来试验方法逐渐趋于统一,但热应力疲劳试验设备和方案的不同使得评价方式有所不同。国内外研究结果均表明,定量计算正逐渐取代定性测量,成为热应力疲劳寿命的研究热点。
(1)依据规定标准下的试验次数评价法。 此方法根据规定循环条件下热应力疲劳裂纹扩展的长度或密度,或是根据达到热应力疲劳裂纹规定长度的试验次数来评价热作模具的热应力疲劳性能[10]。此方法的优点是常常应用于定性分析一种试验方案中不同工艺对材料热疲劳性能的影响,缺点是应力应变采集及过程监控的缺失使得此方法不适用于热应力疲劳过程的研究,更无法支撑定量计算的需求。
(2)图谱评价法。瑞典Uddeholm热疲劳试验的图谱评价法早已应用于工程应用,我国依据原图谱法制定了国家标准GB/T 15824—2008,标准的热作模具棒状试样在完成热疲劳试验后,参考标准图谱对表面龟裂程度进行比较评级。热疲劳裂纹图谱有网状裂纹和主裂纹2个标准,每个标准各有10级,级别越高表明热疲劳损伤程度越严重,试样热疲劳的级别是2个标准下各自评出的级别之和。李新城等[11]基于多种热作模具材料的性能和热疲劳评级,采用偏最小二乘法预测了模具的热疲劳寿命。图谱评价法直观便捷,考虑了裂纹局部的宽度和整体的广度,但它受主观因素影响较大,且具有难以定量化的缺点而限制了其应用。
(3)疲劳损伤因子。 国内外学者基于热疲劳图谱提出了热疲劳损伤因子,来对热疲劳性能进行评价。MELLOULI等[12]通过测量试样端面裂纹深度、宽度和长度来评定热疲劳损伤。郭冰峰等[13]为减少测量工作量,只选取每个试样端面上3条最大裂纹的长度、深度和宽度进行测量,设定三者之积作为损伤因子D,并采用这3条裂纹的损伤因子最大值和平均值分别评价热疲劳损伤程度,研究结果表明,损伤因子的数值越大,损伤程度越严重,热疲劳性能也就越差。然而上述2种方法均忽略了裂纹密度的影响,尤其在网状裂纹情况下,裂纹密度对热疲劳损伤的影响更为显著。吴晓春等[14-15]研究了热作模具热疲劳性能,对图谱的缺点进行了分析,采用图像处理和计算机技术提出了热疲劳损伤因子的概念,弥补了图谱定量分析的不足;他们最先提出了损伤因子D的二维表达式(D=AW,其中A为图谱中裂纹面积的百分比,W为裂纹宽度的平均值),在考虑热疲劳裂纹的总长度和深度后,通过计算机辅助平台计算得到热作模具的热疲劳损伤因子D,即
D=DsDd
(1)
Ds=AWmax/LDd=Pdmax/d5A
式中,Ds为表面损伤因子;Dd为深度损伤因子;Wmax为最宽裂纹的尺寸;L为裂纹的总长度;P为裂纹深度方向的面积百分比;dmax为最深裂纹的深度;d5A为深度值排名前5的裂纹深度平均值(考虑最深裂纹的偶然性)。
此方法能更加全面地反映三维下的裂纹情况,更为客观地体现出热作模具的热疲劳损伤程度,D值越大表明热疲劳损伤越严重。
(4)热疲劳裂纹扩展。 由于难以在线观察和测量裂纹的扩展情况,因此有关热疲劳裂纹扩展的研究相对复杂。热疲劳裂纹的扩展与其他裂纹扩展相似,其扩展速率可采用经典的Paris-Erdogan公式[16]描述,即
da/dN=c(Δk)n
(2)
式中,da/dN为热疲劳裂纹扩展速率(其中a为裂纹长度,N为热疲劳循环次数);Δk为裂纹前端热应力场强度因子幅度;c、n均为与材料等相关的常数,可以通过多组试验数据拟合得到。
当材料强度越高,特别是晶粒较细时,前期热疲劳裂纹萌生时间可达总疲劳寿命的80%;材料强度越低时,热疲劳裂纹扩展越快。但针对热作模具热疲劳裂纹扩展寿命评估的研究很少,许多研究者倾向于对其扩展机理进行研究[17]。
(5)能量理论。 物系运动的熵守恒定律和能量守恒定律同样适用于热疲劳寿命问题。能量法可分为塑性应变能理论、总应变能理论和耗散能理论。冷热疲劳过程中试样产生变形,变形所需的能量为总应变能,包括弹性应变能和塑性应变能。冷热循环过程中试样产生滞后热应力,每一次循环中平均应力的大小决定了弹性应变能的增加或减少,将修正后的弹性应变能与塑性应变能相加得到总应变能。每一次热循环材料都积累一部分应变能,当累积应变能超过材料所能承受的总应变能时,材料热疲劳失效。LEFEBVRE等[18]根据大量试验验证了总应变能理论(包括弹性应变能)比塑性应变能理论更能准确地表征热疲劳寿命。
3 热机械疲劳
热机械疲劳同时存在温度和机械载荷的循环变化,其变形及失效机制与热应力疲劳相比更为复杂。近年来关于热机械疲劳的寿命评估模型有多种,唯象寿命模型和损伤累积模型是主要的两种类型。唯象寿命模型是宏观的物理表征,不用深入研究失效机理也可很好地预测寿命;损伤累积模型则是基于损伤机制综合考虑热机械疲劳损伤各因素的有效寿命预测方法。
3.1 唯象寿命模型
唯象寿命模型是基于唯象描述方法发展而来的,应力-应变滞后回线、应变-寿命曲线和应力-寿命曲线是最常用的描述手段,采用不同的应力或应变范围描述热机械疲劳寿命可得到相应的寿命方程。
(1)基于M-C公式的预测模型。 热机械疲劳属于低周疲劳范畴,适用于低周疲劳寿命的M-C公式同样广泛应用于热机械疲劳。为了更准确地表征热机械疲劳寿命,许多学者依据热机械疲劳的服役特点,对M-C公式进行修正并推导出热机械疲劳寿命模型。COFFIN[19]考虑变温情况下弹性应变、高温蠕变及变温频率对模型的影响,并对M-C公式进行修正,修正后的M-C公式可表示为
(3)
Δεe+p+c=Δεe+Δεp+Δεc
式中,Δεe为循环弹性应变幅;Δεp为循环塑性应变幅;Δεc为循环蠕变应变幅;Nf为材料疲劳断裂的循环次数;ν为交变频率;n、k、C均为与材料相关的常数。
在恒应变热机械疲劳过程中,应力应变循环具有滞后回线,每一个循环过程中吸收的非弹性应变能的积累使得热机械疲劳寿命缩短,这部分能量可通过拉伸半滞后回线的面积ΔU来衡量(即应变能)。施占华等[20]发现恒应变控制试验具有未考虑材料强度的缺点,故用应变能代替非弹性应变范围Δεin作为损伤量来修正M-C公式,推导出如下表达式:
(4)
OSTERGREN[21]则将半滞后回线中的塑性应变幅Δεp和最大应力σmax联合作为损伤量,得到修正后的M-C公式,其表达式如下:

(5)
PAN等[22]在Ostergren模型的基础上考虑了热机械疲劳加载的具体情况,用最大应力σmax和平均应力σm联合表述不同相角条件下的热机械疲劳寿命,得到修正后的M-C公式,其表达式如下:
(6)
式中,α、β、η均为材料常数。
TAIRA等[23]依据等温疲劳试验数据,基于M-C公式引入幅值系数δ,构建了新的热机械疲劳寿命模型,该模型更加简单、实用,其表达式如下:
(7)

上述基于M-C公式的预测模型应用方便,但需要大量的试验数据作为支撑。
(2)应变范围划分法。 HALFORD等[24]考虑到实际构件在服役条件下受到复杂载荷和温度波形的作用,提出了应变范围划分(strain-range partitioning,SRP)法和总应变范围划分(total-strain-range partitioning,TSRP)法。该方法来源于等温疲劳寿命预测,基本思路是将热机械疲劳中塑性应变和蠕变应变用阶梯应力法区分开,两种应变与拉压交变载荷组合在一起,将非弹性应变划分为4种循环,如图2所示。再利用等温低周疲劳实验分别得到材料在4种循环条件下的寿命,热机械疲劳寿命分数就可由相应的4种低周疲劳寿命分数线性叠加得到,即
(8)
Fij=Δεij/Δεini,j=c,p
式中,Δεpp为拉伸压缩均为塑性变形类型的应变范围;Δεcc为拉伸压缩均为蠕变变形类型的应变范围;Δεpc为拉伸塑性变形与压缩蠕变变形类型的应变范围;Δεcp为拉伸蠕变变形与压缩塑性变形类型的应变范围;Nij为4种不同应变循环条件下的低周疲劳寿命。

(a)均为塑性变形 (b)均为蠕变变形

(c)拉伸塑性变形与压缩蠕变变形 (d)拉伸蠕变变形与压缩塑性变形图2 4种基本的应力-应变类型Fig.2 Four basic stress-strain types
(3)应变能划分法。 SRP法仅适用于应变控制条件下的热机械疲劳寿命预测,对于塑性应变小和保温时间短的材料,何晋瑞等[25]基于Ostergren损伤函数提出了应变能划分(strain-energy partitioning,SEP)法。SEP法的理论前提是:材料非弹性应变能是决定蠕变-疲劳损伤的根本原因,决定寿命的不是总的非弹性应变能,而是蠕变应变能和塑性应变能,只有拉伸滞后能才能引起损伤促使裂纹扩展。董照钦等[26]从应变能的角度建立了应变能频率分离模型,指出引起时间相关疲劳损伤的主要是材料拉伸部分的非弹性应变能。胡绪腾等[27]等借鉴TSRP法的推导经验,将SEP法拓展推广到总应变形式,提出了总应变-应变能划分法,拓展了SEP法的适用范围。SEP法在国际上得到了美国材料与试验协会(American society for testing materials, ASTM)的肯定,许多学者也逐渐采用能量法对高温合金进行寿命预测且得到了很好的效果,但需要明确滞后环的形状以及得到相应的研究数据。
3.2 损伤累积模型
国内外学者提出了很多应用于低周疲劳的损伤累积理论和计算模型,而关于热作模具热机械疲劳寿命的研究并不多,都是依据高温低周疲劳推导而来。疲劳损伤累积理论的核心就是定义损伤变量,热机械疲劳失效是由交变温度和机械载荷所产生的损伤循环累积而造成的,塑性应变、与时间相关的蠕变和应变能等均可设为损伤变量,再结合材料在温度下的应力-应变关系即可构建寿命预测模型。根据损伤累积路径的不同,疲劳损伤理论分为线性和非线性,线性理论因简单易用而应用广泛,非线性理论的准确性高但较为复杂。
(1)线性损伤累积模型。 基于高周疲劳中经典的Miner理论对热机械疲劳中的损伤作用进行累积,总损伤达到1即表明材料破坏失效。将热机械疲劳损伤记为疲劳损伤分数φf与蠕变损伤分数φc之和,损伤分数为某个控制水平下的循环次数与该水平作用下材料疲劳寿命之比,其表达式如下:
φf+φc=1
(9)

(2)非线性损伤累积模型。 许多实验表明线性累积损伤模型的误差仍然较大,且并非所有材料均满足上述线性损伤累积方程。有学者考虑到蠕变-疲劳的交互作用,故在式(9)的基础上增加一个交互作用项,修正后的表达式如下:
(10)
其中,B为交互作用系数,其大小直接反映蠕变-疲劳交互作用的强弱。而针对蠕变-疲劳交互作用,许多学者开展了深入研究并构建了寿命预测模型[28-29]。
在低周疲劳损伤累积模型中,将物理性能指标作为损伤变量来构建能量耗竭、韧性耗竭和延性耗竭三种寿命损伤理论。热机械疲劳中存在温度变化,材料临界韧性和临界延性极难确定,而基于能量的损伤累积模型能更加方便和准确地描述热机械疲劳寿命。施惠基等[30]根据热机械疲劳的基本特征和应力-应变关系,基于非线性黏-弹塑性运动强化模型描述方法,将循环应变能密度作为损伤参量,引入温度的影响,对微小单元的损伤累积进行计算,并推导出与循环相关的热机械疲劳寿命预测模型,其表达式如下:
(11)
式中,ΔΨTMF为单次循环的损伤量;Nf,T0为参考温度T0下等温疲劳破坏循环周次;σTi为微小单元在温度Ti时的应力幅值;ΔεσTi为微小单元应力幅值对应的应变增量;ΔWt,Ti为在温度Ti时的等温疲劳循环应变能密度;λ(Ti)为引入的温度损伤系数,可以从对应的等温疲劳寿命中求出。
此方法理论上较为严谨,但模型的建立需要大量的高温低周循环疲劳试验数据,因此限制了该方法的应用。
损伤力学作为连续体力学的一个分支,以热力学为基础,借助数学和力学建立表征损伤过程的损伤发展方程,该方法因突破了根据试验结果建立经验公式的传统方法而得到了广泛应用。CHABOCHE等[31]首次将连续损伤力学方法系统地应用到疲劳寿命预测中,其后LEMAITRE等[32]、WANG等[33]依据连续损伤力学先后提出了不同的疲劳损伤演化方程。在损伤力学方面,针对热作模具热机械疲劳的研究较少,SOMMITSCH等[34]对Chaboche模型进行了修正,并构建了热作模具的疲劳寿命模型;方健儒[35]结合Taira等效温度法修正了Chaboche模型,用以表征热作模具的热机械疲劳寿命,且取得了良好的预测效果,该模型的表达式如下:
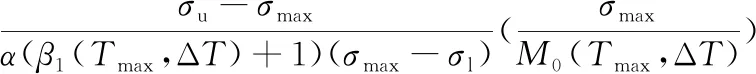
(12)
式中,α为材料常数;σu为材料抗拉强度;σl为拉压对称疲劳极限强度;Tmax为材料经历的最高温度;ΔT为材料经历的温度循环范围;β1、M0均为与温度相关的函数。
根据式(12),设等效温度Te时的等温疲劳与热机械疲劳产生的损伤量相同,M0可从等温疲劳试验中获得,β1用来表征热循环产生的附加损伤量,由热疲劳应力可计算得到。
一些学者综合考虑平均应力、内应力、疲劳-蠕变交互作用等因素,结合唯象描述和损伤累积模型对金属材料的热机械疲劳进行了寿命评估[36],并获得了良好的匹配度。应力-应变关系主要由周期性的应力屈服曲线(拉伸过程)和应力松弛曲线(保载过程)两部分组成,分别利用Ramberg-Osgood方程和Norton-Bailey方程唯象描述并得到应力-应变滞后环关系。热机械疲劳损伤根据Robinson/Taira损伤积累模型分为疲劳损伤Ψf和蠕变损伤Ψc,并根据临界损伤值Ψcrit判断寿命,其表达式如下:
Ψ=Ψf+Ψc≤Ψcrit
(13)
其中,疲劳损伤Ψf根据Palmgren和Miner理论得到迟滞环对应的损伤量;蠕变损伤Ψc依据Robinson理论累积应力松弛每个时间段的蠕变损伤量;临界损伤值Ψcrit则通过如下方式获得:材料经高温拉伸卸载试验得出临界应变值,并采用Normalized Cockcroft & Latham准则数值模拟高温拉伸至临界应变状态,以确定材料在热变形条件下的临界损伤值[37]。
4 主要问题和展望
热作模具在服役过程中会经历温度的交替变化以及加工周期中载荷的变化,热应力疲劳寿命和热机械疲劳寿命的研究将直接影响到热作模具材料的经济使用,准确的寿命评估与预测可以保证生产系统的连续稳定。在以理论为指导的工程应用方面,高强材料的大批量生产需要更为准确的模具服役信息,而热作模具的研发需要更为精准的性能提升方向,热作模具热疲劳的寿命研究具有前瞻性和经济性。
虽已在热作模具热疲劳寿命评估和预测方法的研究中取得了不少成果和进展,但在热作模具试验及应用过程中,针对其中一些关键问题,仍需展开系统和深入的研究。
(1)研究新的测试技术。由于高温环境下测试技术的不成熟,故目前还不能准确地测量高温温度场的变化、模具表面形貌的实时演变以及热状态下模具内部应力-应变状态等试验验证寿命的关键数据,这些因素将制约热疲劳寿命的研究。为了更好地描述试验结果和控制试验环境,不损坏试验流畅、同步在线监测和原位分析等技术已日益成为热作模具热疲劳试验的迫切需求。
(2)热作模具热机械疲劳寿命的系统化研究。热机械疲劳寿命研究是多因素的复杂课题,系统化的研究可极大程度地指导热作模具生产应用:首先,从单因素的热应力疲劳、高温疲劳研究,到多因素复合的热机械疲劳研究;再者,针对热作模具加压-保压的载荷施加特点以及温度交变特点,分别从宏观和微观探求模具材料的变形机制,提出有效的寿命评估预测方法;最后,在数值模拟与数理统计中寻求有效的方法,对试验数据进行有效的采集和处理,以得到更精准的热作模具热机械疲劳寿命预测方程。
(3)工况下模具热疲劳寿命的研究。在服役过程中,热作模具的热疲劳寿命并不等价于试验中模具材料的热疲劳寿命,现有热疲劳试验还不能完全再现工作中热作模具的状态。比如:热作模具表面产生的网状裂纹在外界接触和摩擦的作用下会发生脱落或折叠[38];高强材料在模压过程中会产生界面传热、摩擦和塑性变形,以及发生温度变化[39];试样和模具尺寸与形状的不同会造成热应力和机械应力的分布不一致等。结合模具材料的热疲劳特性,使用有限元软件构建热作模具及复杂的温度场、应力场是理想的方式,但对热作模具表面损伤、多因素复合作用和使用寿命预测的准确表征还需更加深入的研究[40]。
总之,热作模具热疲劳寿命的研究涉及力学、计算数学、材料、化学甚至物理学等交叉学科的理论与试验,需从宏观到微观、数值模拟和物理试验等多层次上的结合进行研究与分析。
5 结论
(1)本文介绍了热作模具热疲劳研究的现状:模具材料热应力疲劳性能评价已成体系,可以定量地评估和预测不同材料在特定参数下的使用寿命;从基于大量试验的唯象寿命描述角度出发,热机械疲劳寿命评估及预测的研究已向考虑主要损伤机理的综合损伤模型表征方向发展。
(2)基于热应力疲劳研究,学者通过构建损伤因子、研究裂纹扩展及能量理论等手段定量地评价及预测热疲劳寿命。唯象描述的热机械疲劳寿命预测模型日渐成熟,主要包括基于M-C公式的修正模型、应变范围划分法及应变能划分法;而损伤累积模型从损伤机理出发,将热疲劳损伤区分并通过高温拉伸、蠕变等基础试验定量化后,按照损伤路径线性或非线性累加,得到的预测效果优良,但国内外针对此方面研究的评价方式尚未统一。
(3)在热作模具热疲劳寿命研究成果及进展的基础上,针对实验及应用过程,在新的测试技术、热作模具热机械疲劳寿命的系统化研究、工况下模具热疲劳寿命的研究三方面进行了展望。

