一种黏土层中深基坑开挖地表沉降预测方法

胡之锋，陈 健，邱岳峰，李健斌

(1.中国科学院武汉岩土力学研究所 岩土力学与工程国家重点实验室,武汉 430071；2.中国科学院大学, 北京 100049)

1 研究背景

随着经济的持续发展，城市化进程不断加速，人口暴增、交通拥堵、土地紧张等问题日益突出。为缓解矛盾，高层建筑、地铁工程、地下商场等工程项目不断增多，规模越来越大，城市建设过程中正涌现出越来越多的深基坑工程。这些基坑多位于城市中心，紧邻建筑物、城市道路以及城市地下管线，基坑开挖易对这些建(构)筑物及市政设施造成不利影响。地表沉降作为一个重要的变形控制指标对保护基坑周边环境具有重要意义，因而，地表沉降预测一直受到众多研究人员的重视。

目前，诸多学者通过广泛深入研究，已经发展并形成了一系列地表沉降预测方法，主要包括经验预测法、数值模拟法、理论解析法和地层损失法。

经验预测法方面，Peck[1]、Clough等[2]、Ou等[3]、Hsieh等[4]、Wang等[5]、Wang等[6]、王卫东等[7]通过收集大量工程实测数据，运用统计分析方法，分别绘制出了一系列地表沉降预测曲线，提出了针对不同地区的地表沉降经验预测公式。数值模拟法方面，Kung等[8]、杨敏等[9]、Ou等[10]、尹盛斌等[11]、王卫东等[12]运用数值计算软件，对基坑开挖地表沉降变形规律进行研究，总结出了针对不同地区、不同地质条件、不同支护结构形式的地表沉降预测方法。理论解析法方面，钱建固等[13]、顾剑波等[14]、沈路遥等[15]从弹性边值问题出发，分别推导出了围护结构刚性变形、抛物线柔性变形和任意变形模式下的地表沉降解析表达式。地层损失法方面，自Peck[1]首次提出该方法后，Bowles[16]将其应用于拱肩型地表沉降预测，刘建航等[17]将其应用于凹槽型地表沉降预测，此后，诸多学者将其应用于全国各地深基坑工程地表沉降计算中。此外，周永胜[18]、朱靓[19]、王雪妮等[20]还运用各种不同的智能预测模型对基坑变形进行了预测分析。

总体而言，上述几类方法中，基于工程实测数据的统计分析方法、基于有限元的数值模拟方法、基于地层损失理论的地层损失法以及基于智能预测模型的智能方法均被广泛应用于实际工程中，而基于弹性边值问题的理论解析法在实际工程中应用较少。

刘建航等[17]认为，基坑围护结构变形是引起周围地层变形的主要原因之一，目前以围护结构水平位移为边界条件，基于线弹性理论的解析式在预测黏性土基坑地表沉降最大值位置方面与实测数据较为吻合。本文利用解析解的这一特点，与地层损失法相结合，综合运用这2种方法来预测地表沉降，基本思路简要概括如下：首先根据既有研究假设地表沉降曲线分布函数；然后运用解析表达式求出地表沉降最大值位置xm，结合既有经验计算地表沉降影响范围x0；再推导出地表沉降面积Av，计算出围护结构侧移面积Ah；最后根据Av和Ah之间的相关关系，计算地表沉降最大值δmax，从而由假设沉降曲线估算墙后任意位置的地表沉降。

2 计算方法介绍

根据既有研究，以凹槽型地表沉降为研究对象，首先假设墙后地表沉降曲线为正态分布概率密度函数；然后根据围护结构水平变形，利用平面应变边值条件下的解析表达式求出地表沉降最大值位置xm；进而通过假设沉降函数，结合相关经验，确定地表沉降影响范围x0；在得到xm和x0后，对假设沉降曲线函数进行积分运算，推导出地表沉降曲线包络面积Av表达式；然后由围护结构水平位移曲线算出围护结构侧移面积Ah；再根据Av与Ah之间的相关关系，计算地表沉降最大值δmax；将δmax代入假设函数即可预估墙后任意处的地表沉降。下面将按步骤、分章节对该方法的计算过程作详细介绍。

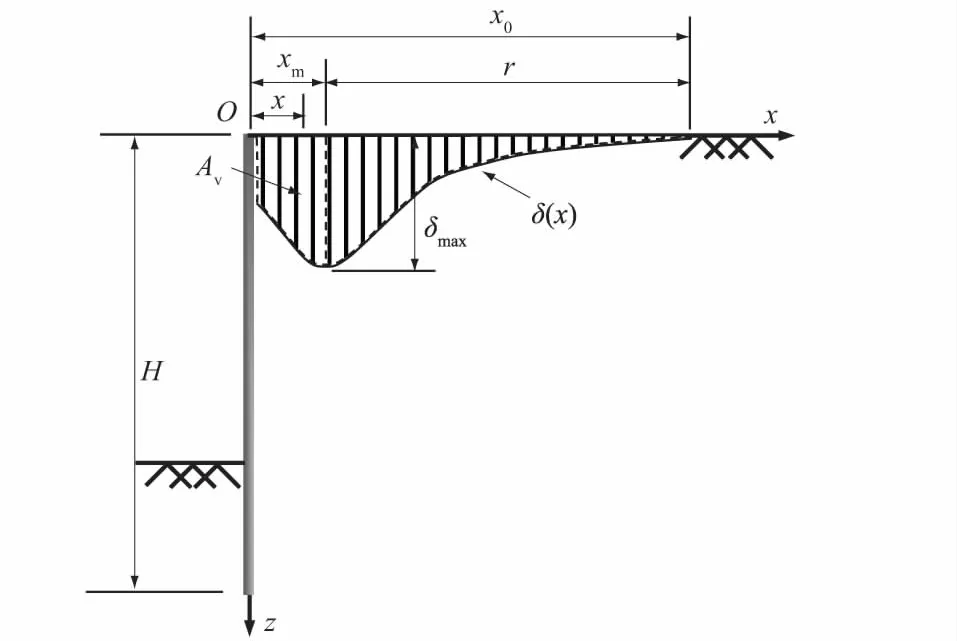
图1 假设地表沉降模型Fig.1 Sketch of assumed ground settlement model

2.1 地表沉降曲线假设

目前，深基坑第一道支撑多采用钢筋混凝土支撑，围护结构顶部受到约束，开挖时，围护结构水平位移一般表现为弓形变形，墙后地表沉降曲线呈现出凹槽型特性。本文以凹槽型地表沉降曲线为研究对象，根据既有研究[21-27]，假设墙后地表沉降曲线为正态分布概率密度函数，表达式为

(1)

式中：各参数意义如图1所示。δmax表示地表沉降最大值；xm表示地表沉降最大值位置距基坑边缘的距离，即地表沉降最大值位置；x表示墙后任意点到基坑边缘的水平距离；r表示沉降盆影响半径，r=x0-xm，其中x0表示地表沉降影响范围。

2.2 地表沉降最大值位置计算

地表沉降与基坑围护结构水平位移密切相关，本文基于平面应变边值条件下的解析表达式，以围护结构水平位移为边界条件，计算地表沉降最大值位置xm，具体计算过程参考沈路遥等[15]的做法，主要步骤如下。

第1步：把基坑围护结构从上到下划分为n个微段，将每一个微段发生的变形都看成平移变位模式，如图2所示。

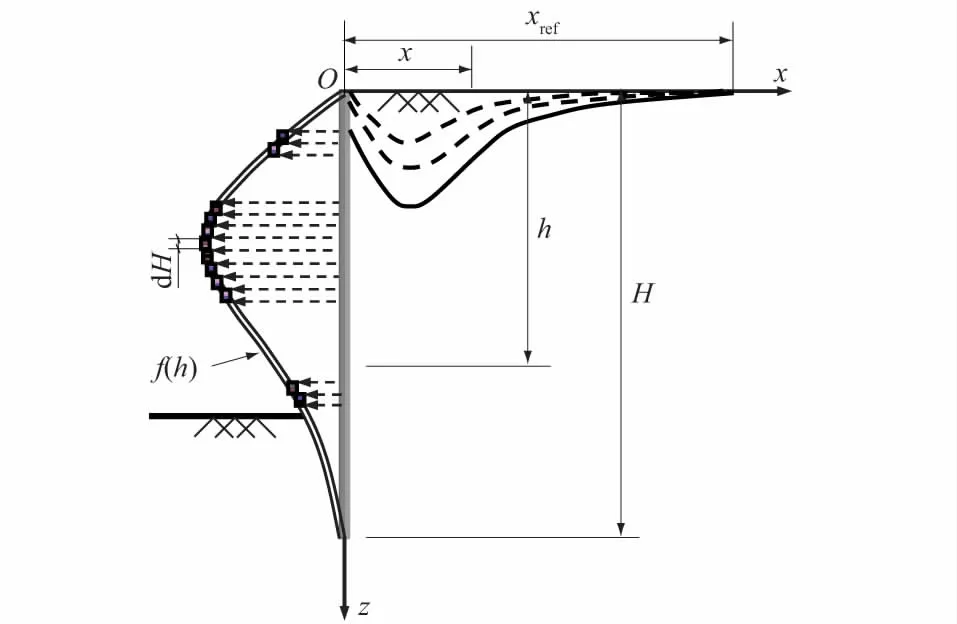
图2 围护结构水平位移曲线微段划分[15]Fig.2 Diagram of micro-segments by dividinghorizontal displacement curve of retaining wall[15]

第2步：利用围护结构平移变位模式诱发地表沉降解析解式(2)推导出围护结构任意微段平移所产生的地表沉降值，沉降计算示意图如图3所示。

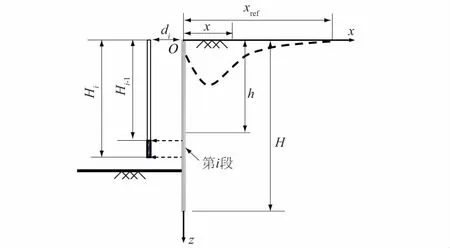
图3 挡墙任意微段平移诱发地表沉降等效计算[15]Fig.3 Diagram of ground settlement caused by horizontal displacement of any micro-segment ofretaining wall[15]

图2、图3中的符号说明如下：H，h分别表示围护结构长度和任意点到围护结构顶部的距离；x表示墙后任意地表点到墙背的水平距离；xref表示线弹性条件下位移为0的点到墙背的水平距离；Hi和Hi-1分别为第i段底部和顶部的高度;di为第i微段的等效水平位移距离，可对微段底部和顶部水平位移取平均值求得。

基坑围护结构平移变位模式诱发地表沉降解析解[13]如式(2)所示，即

(2)

当i=1时，为围护结构顶部的第1微段，可利用式(2)直接求解，即

(3)

式中：d1为基坑围护结构第1微段水平位移的等效平移值；x1_ref假设为10H1[13]。

当i≥2时，可分别计算深度为Hi和Hi-1时，围护结构水平变位诱发的地表沉降值为：

(4)

对于各种深度的围护结构，其平移对地表沉降产生的影响范围均假设为该深度的同一倍数，参考文献[13]假设为10倍，即xi_ref=10Hi，xi-1_ref=10Hi-1，代入式(4)、式(5)并对二式求差运算，可得围护结构任意微段(i≥2)平移引起的地表沉降值为

第3步：对围护结构各微段平移引起的地表沉降值Δwi进行叠加求和，便可计算出围护结构整体水平位移诱发的地表沉降值，即

(7)

根据式(3)、式(6)、式(7)，编写程序可得到地表沉降最大值位置xm。

2.3 地表沉降影响范围计算

运用地层损失法预测基坑开挖地表沉降时，地表沉降影响范围x0取值不能过大，也不能太小。因为围护结构侧移面积Ah是一定的，根据地表沉降面积Av与围护结构侧移面积Ah之间的相关比例关系计算所得的Av也是一定的。如图4所示，如果地表沉降影响范围x0取值过大，计算所得的地表沉降曲线会被拉长，在基坑主要影响范围内曲线会变平缓，低估地表沉降值；反之，地表沉降曲线会被缩短，在基坑主要影响范围内曲线会变急陡，高估地表沉降值。

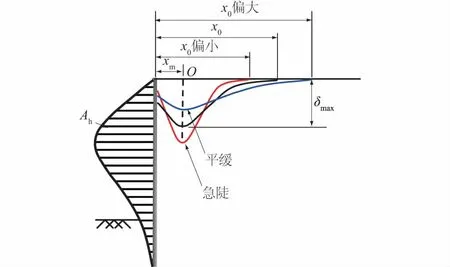
图4 影响范围取值大小对地表沉降的影响Fig.4 Sketch of ground surface settlement curve in influence zone of different sizes

本文通过对既有文献[4,6-8]统计分析所得地表沉降预测曲线进行深入研究发现，不同学者根据统计数据所确定的地表沉降影响范围有所差异，但主、次要影响区分界点较为集中，均位于墙后2倍基坑开挖深度处(2He)，大小约为地表沉降最大值δmax的0.1，如图5。因此，为了使假设沉降曲线能准确预测墙后主要影响区内的地表沉降，本文以基坑主、次要影响区分界点为依据，结合2.2节所求地表沉降最大值位置xm，确定地表沉降影响范围。

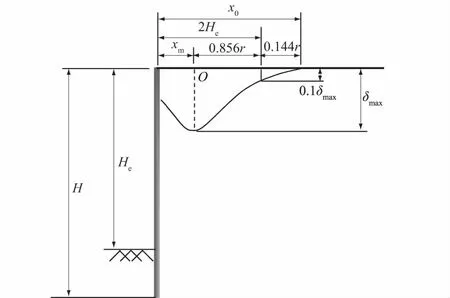
图5 沉降影响范围x0求解示意图Fig.5 Sketch of calculating x0 in assumed ground settlement function

首先将坐标(2He，0.1δmax)代入式(1)得

(8)

如图5所示，根据地表沉降曲线各特殊位置几何关系可得

xm+xp=2He。

(9)

式中：xp表示地表沉降最大值位置到主、次要影响区分界点的水平距离;He为基坑开挖深度。

由式(8)、式(9)可得

xp=0.856r。

(10)

根据r=x0-xm，结合式(9)、式(10)可得

0.144xm+0.856x0=2He。

(11)

将基坑开挖深度He和上节所求xm代入式(11)即可算出基坑开挖影响范围x0。

2.4 地表沉降曲线包络面积计算

在获得地表沉降最大值位置xm和地表沉降影响范围x0后，通过对假设沉降曲线函数进行积分运算，可推导出只包含未知数δmax的地表沉降曲线包络面积Av。为计算方便，设xd=x-xm，将坐标原点临时变换到地表沉降最大值位置处，则Av积分表达式为

(12)

式(12)经过变换后可得

(13)

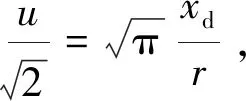
(14)

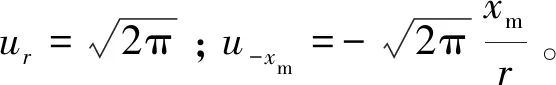
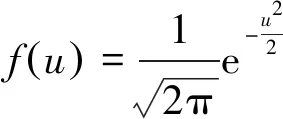
Av=δmaxr[Φ(ur)-1+Φ(uxm)] 。

(15)

式中Φ(u)为标准正态分布函数。

把ur代入可得

(16)

则式(16)可写为

(17)

地表沉降最大值位置xm和地表沉降影响范围x0已经分别在第2步和第3步求出；r=x0-xm，可由x0和xm算出。因此，地表沉降曲线包络面积Av只包含未知数δmax。

2.5 围护结构侧移面积计算

围护结构侧移面积Ah可分2步计算：首先根据围护结构水平位移实测数据，拟合得到水平位移曲线表达式；然后对所得拟合函数在围护结构长度范围内积分即可求出侧移面积Ah。目前围护结构水平位移一般采用多项式拟合，文献[28]在对基坑围护结构水平位移曲线进行拟合研究时发现运用5次多项式拟合误差能达到最小，因此本文采用5次多项式拟合围护结构水平位移曲线，从而计算围护结构侧移面积Ah。如图6所示，将坐标原点设在围护结构顶端，f(h)表示围护结构水平位移曲线拟合多项式函数，则围护结构侧移面积Ah可表示为

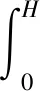
(18)

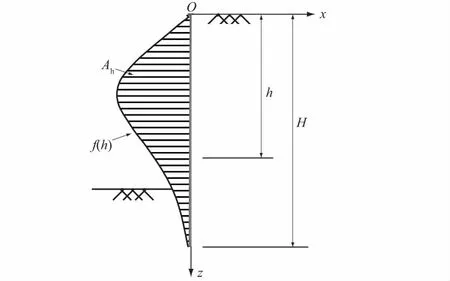
图6 围护结构侧移面积计算Fig.6 Sketch of lateral horizontal displacement area of retaining wall

2.6 地表沉降最大值计算

根据式(18)计算围护结构侧移面积，由地表沉降面积Av和围护结构侧移面积Ah之间的相关性，结合已经推导出的地表沉降面积Av表达式(17)，便可计算出地表沉降最大值δmax。

其中，地表沉降面积Av和围护结构侧移面积Ah之间的相关关系由面积比β建立，β一般通过经验确定，定义为

Av/Ah=β。

(19)

计算出地表沉降最大值δmax后，将δmax，xm和r代入式(1)即可得到地表沉降预测曲线函数，从而可方便地估算出墙后任意地表位置的沉降值。

3 工程实例应用

为了说明上述方法的工程适用性，将借助工程实例加以验证，并与其他方法进行对比分析。在此之前，需对沉降计算方法中的面积比β加以说明。

目前，β一般借助经验确定，软土地区经验丰富，对于比值β的研究较多：刘建航等[17]结合上海地区工程经验，建议在围护结构采用插入较深的地连墙或者灌注桩时取β=1；彭振斌等[29]通过实测数据证明，基坑开挖孔隙水压力消散后β=0.85；Peck[1]以板桩支护基坑为研究对象，根据统计分析结果得出β=1；Finno等[30]依据芝加哥地铁车站实测数据，发现地表沉降面积与围护结构侧移面积大小相一致，即β=1；此外，聂宗泉等[31]根据统计分析结果，认为β与围护结构插入比有关，当围护结构插入比≤0.5时，β=1.0～1.2，当围护结构插入比>0.5时，β=0.8～1，注意到，文献[31]在工程实例中遇到插入比>0.5的情况时，β值均取0.9。

从既有经验来看，软土地区基坑开挖围护结构侧移面积与地表沉降面积大小基本一致。本文采用解析表达式确定地表沉降最大值位置,文献[14-15]显示其在预测黏土地区地表沉降最大值位置时效果较好，因此本文选用台北、伦敦等黏土地区的工程实例来验证本文方法的工程适用性。目前关于黏土地区β值的研究较少，参考软土地区工程经验，同时考虑到黏土工程特性较软土好以及围护结构插入比大小的影响，本文β取值规则如下：当围护结构插入比<1时，取β=0.85；当围护结构插入比≥1时，取β=0.8。

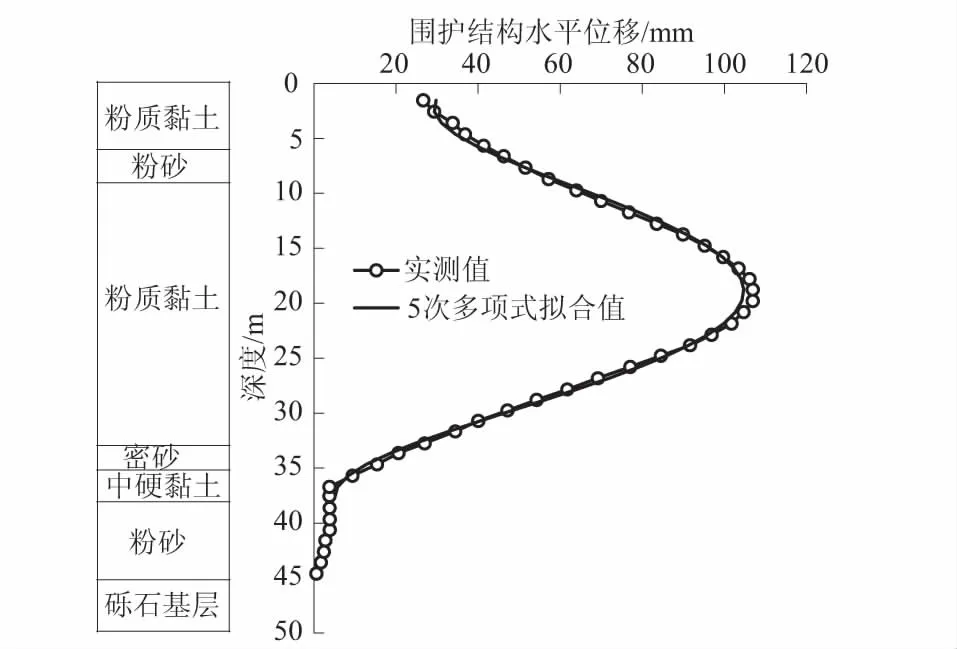
图7 实例1围护结构水平位移曲线Fig.7 Curves of lateral displacement of retaining wall in engineering example 1

3.1 工程实例1[32]

台北名族企业中心(TNEC)位于台北盆地，占地面积3 500 m2，地上18层，地下5层。所处地层主要由粉质黏土和粉砂组成；基坑围护墙长35 m，厚0.9 m，开挖深度19.7 m，采用逆作法施工。

图7给出了围护结构水平位移实测曲线及拟合曲线。注意到，深度约37.5 m以下的围护结构水平位移很小，在多项式拟合时未选取这部分数据。将拟合多项式代入式(18)中可算得Ah=2.31×106mm2；结合拟合多项式，根据式(3)、式(6)、式(7)可求出地表沉降最大值位置xm=13.4 m，继而由式(11)解出沉降影响范围x0=43.8 m，从而可通过r=x0-xm算出r=30.4 m；该工程插入比为0.78，根据既有说明取β=0.85；最后根据式(17)、式(19)并结合围护结构侧移面积Ah，可算出地表沉降最大值δmax=74.7 mm；将δmax，xm和r代入式(1)可得地表沉降预测曲线函数，从而估算墙后任意点的地表沉降值。同时，在本文计算xm值的基础上，根据文献[4,8,24,27]建议的x0取值，分别给出了x0取值为4.0He，2.5He，1.5H时的地表沉降预测曲线，以说明本文计算x0方法的合理性。此外，根据文献[3-4]，假设地表沉降最大值为围护结构水平位移的0.625，给出了文献[4]方法的预测曲线。所得预测曲线与实测值对比如图8所示。

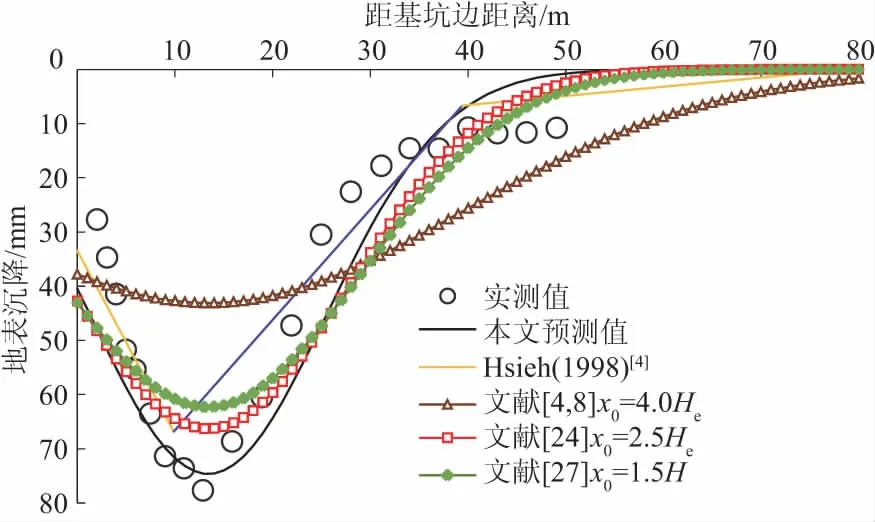
图8 实例1地表沉降预测曲线与实测值对比Fig.8 Comparison between predicted ground settlement curves and measured curve for example 1

3.2 工程实例2(Formosa)[3-4]

该工程位于台北盆地，所处地层主要为黏土，基坑围护墙长31 m，厚0.8 m，基坑开挖深度约18.5 m，采用顺作法施工。围护结构水平位移实测曲线及拟合曲线如图9所示；相关参数的计算、取值过程与工程实例1类似，结果见表1；所得地表沉降预测曲线与实测数据对比如图10所示。

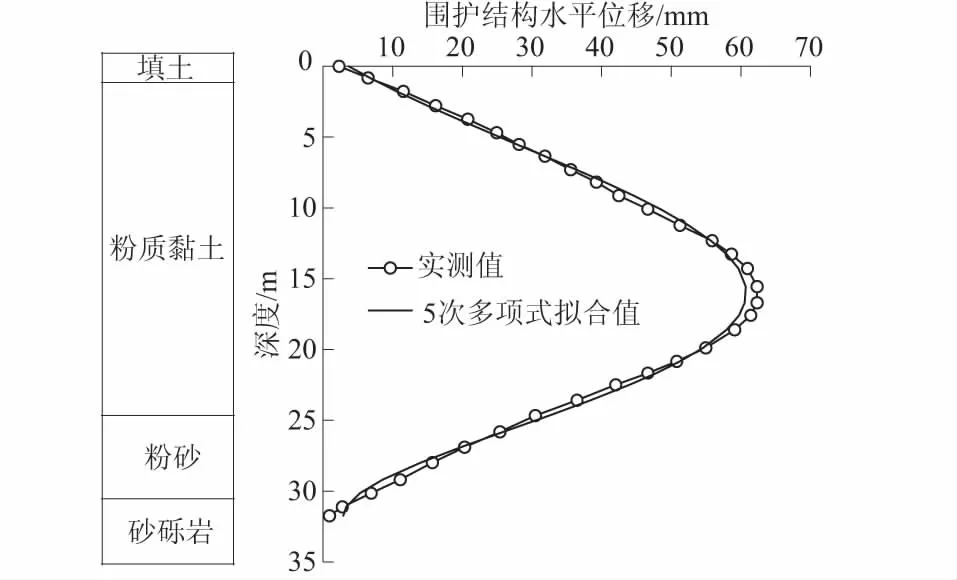
图9 实例2围护结构水平位移曲线Fig.9 Curves of lateral displacement of retaining wall in engineering example 2

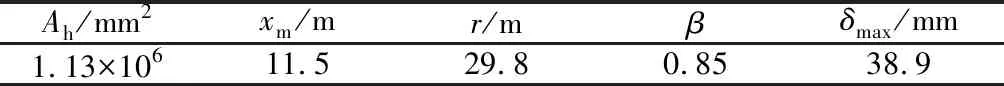
Ah/mm2xm/mr/mβδmax/mm1.13×10611.529.80.8538.9

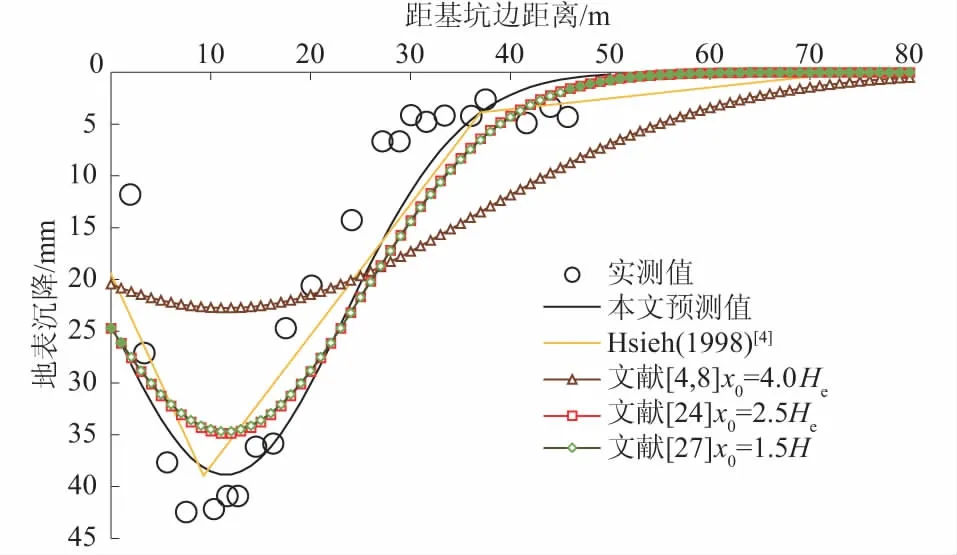
图10 实例2地表沉降预测曲线与实测值对比Fig.10 Comparison between predicted ground settlement curves and measured curve for example 2

3.3 工程实例3[33-34]

该工程位于台北松山，所处地层主要为黏土，基坑围护墙长为33 m，厚1 m，开挖深度约16.2 m，采用顺作法施工。围护结构水平位移实测曲线及拟合曲线见图11；相关参数的计算、取值结果见表2；所得地表沉降预测曲线与实测数据对比见图12。

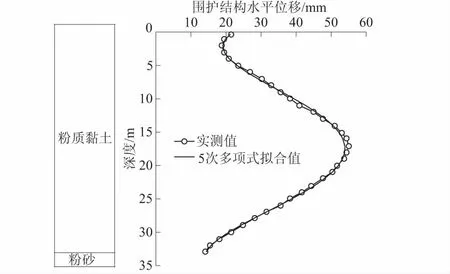
图11 实例3围护结构水平位移曲线Fig.11 Curves of lateral displacement of retaining wall in engineering example 3

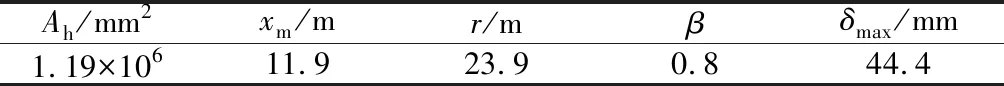
Ah/mm2xm/mr/mβδmax/mm1.19×10611.923.90.844.4

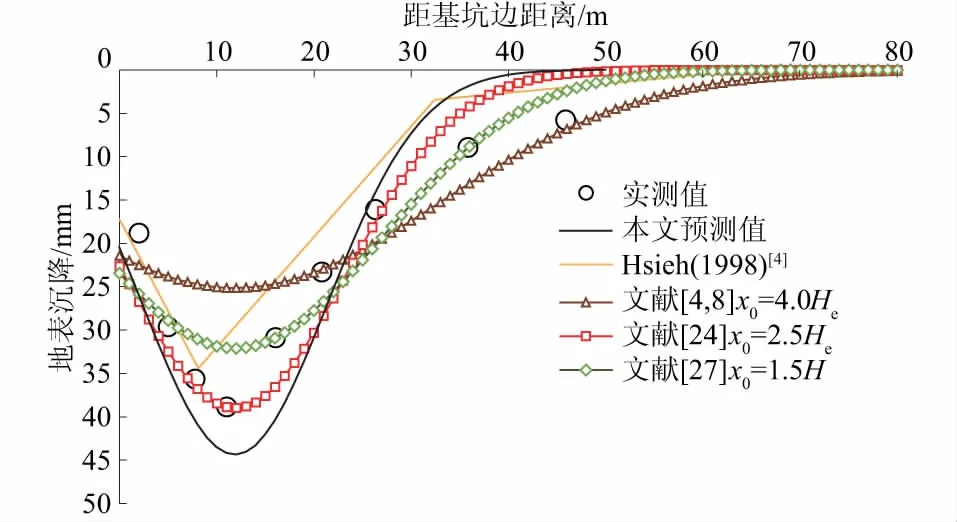
图12 实例3地表沉降预测曲线与实测值对比Fig.12 Comparison between predicted ground settlement curves and measured curve for example 3

3.4 工程实例4(New Palace Yard)[35-36]

该工程位于伦敦，所处地层主要为伦敦黏土，基坑围护墙长30 m，开挖深度约18.5 m，平面形状接近正方形，选取了基坑南向断面A-A’和东向断面B-B’实测数据来验证本文方法的工程适用性。

A-A’断面围护结构水平位移实测曲线及拟合曲线如图13所示；相关参数的计算、取值结果见表3；所得地表沉降预测曲线与实测数据对比如图14所示。

B-B’断面围护结构水平位移实测曲线及拟合曲线见图15；相关参数的计算、取值结果见表4；所得地表沉降预测曲线与实测数据对比见图16。

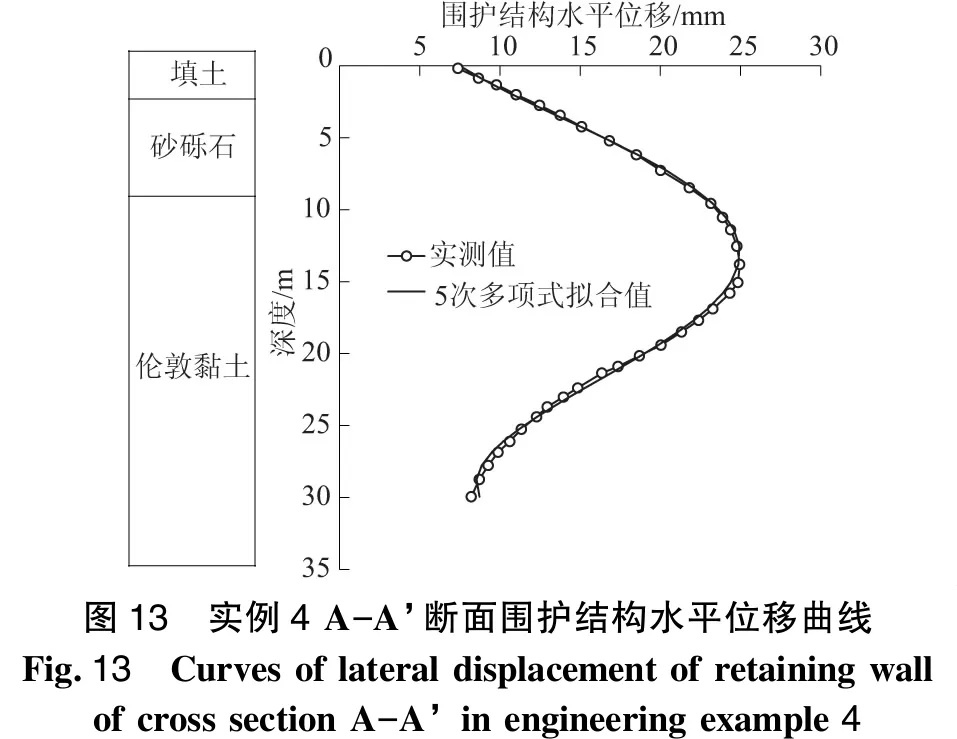
图13 实例4 A-A’断面围护结构水平位移曲线Fig.13 Curves of lateral displacement of retaining wallof cross section A-A’ in engineering example 4

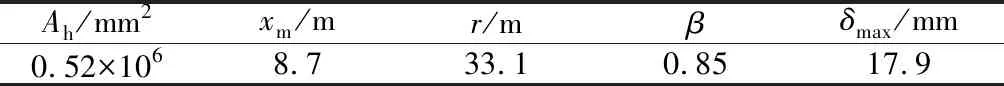
表3 实例4 A-A’断面地表沉降计算各相关参数值Table 3 Summary of parameters involved in the calculation of surface settlement of cross section A-A’ in engineering example 4

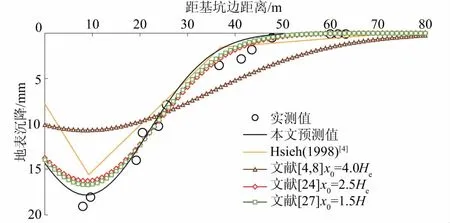
图14 实例4 A-A’断面地表沉降预测曲线与实测值对比Fig.14 Comparison between predicted ground settlement curves and measured curve for cross section A-A’ in engineering example 4

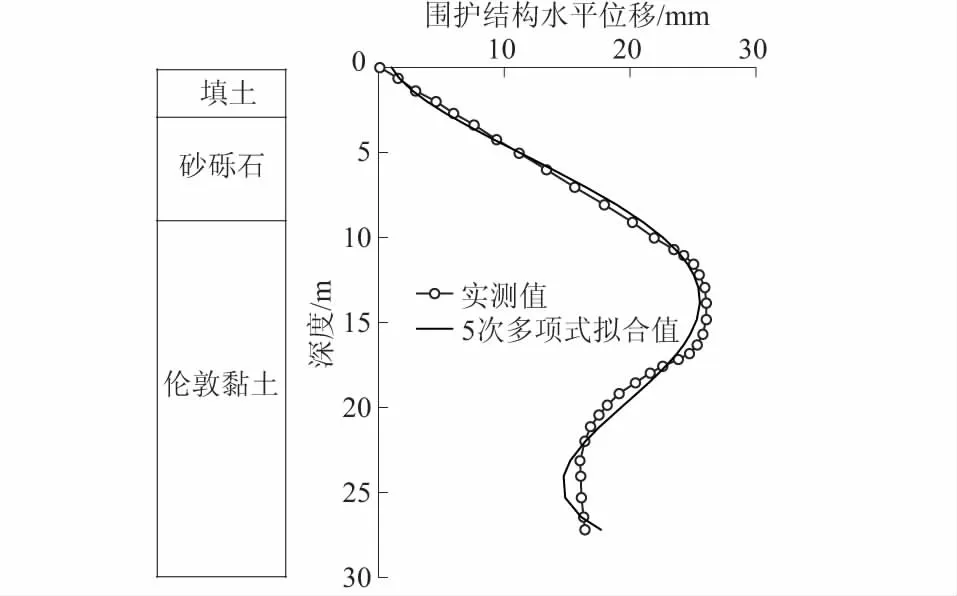
图15 实例4 B-B’断面围护结构水平位移曲线Fig.15 Curves of lateral displacement of retaining wall of cross section B-B’ in engineering example 4

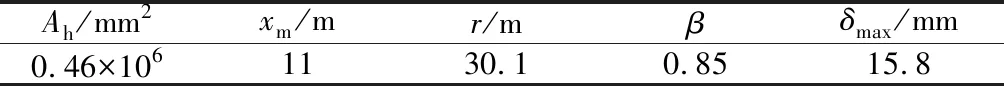
表4 实例4 B-B’断面地表沉降计算各相关参数值Table 4 Summary of parameters involved in the calculation of surface settlement of cross section B-B’ in engineering example 4

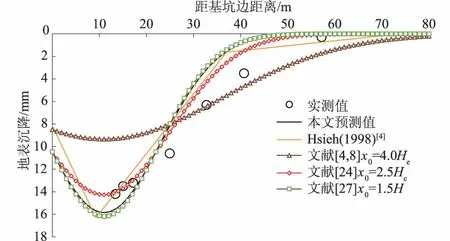
图16 实例4 B-B’断面地表沉降预测曲线与实测值对比Fig.16 Comparison between predicted ground settlement curves and measured curve for cross section B-B’ in engineering example 4

3.5 综合分析

运用上述4项工程5个监测断面的实测数据对本文沉降预测方法进行了验证，见图7—图16，本文预测曲线与实测数据变化趋势基本一致，除图12偏差稍大以外，其余工程案例预测值与实测值整体吻合较好。应注意，由于土体与围护结构之间存在摩擦，土体下沉受到一定程度的阻碍，预测值在坑边局部范围内误差偏大；此外，根据假设曲线计算得到的次要影响区较小，上述实例中最大仅为0.26He，预测函数在次要影响区内较快收敛到0，因此本文方法对基坑次要影响区的预测一般偏小。考虑到基坑次要影响区内地表沉降值一般较小，影响不大，主要影响区内，预测值仅在坑边误差较大，总体而言，本文方法预测效果较好。

对比本文预测曲线与x0取值分别为4.0He，2.5He，1.5H时的计算曲线，可以看出地表沉降最大值xm位置一致时，x0越大，曲线越平缓，计算所得地表沉降值越小，反之亦然。由图7—图16可知，大部分工程实例中，与x0取值分别为4.0He，2.5He，1.5H时的计算曲线相比，本文预测曲线与实测数据更为吻合，说明在本文计算地表沉降最大值位置的基础上，基于主次要影响区分界点计算x0是合理的，这在一定程度上避免了由经验确定x0的不确定性。

将本文预测曲线与Hsieh等[4]的方法对比，可以看出Hsieh等[4]的预测方法在次要影响区内较本文预测方法好，但是由于其假定地表沉降最大值位置xm均为基坑开挖深度的0.5，而未考虑围护结构不同水平变形对地表沉降的影响。从图8、图12可以看出，与本文以围护结构水平位移为边界条件计算xm相比，其效果相对较差，因此在一定程度上导致主要影响区内预测结果较本文方法差。

4 结 论

基于平面应变边值条件下的地表沉降解析表达式，联合地层损失法，针对凹槽型地表沉降，提出了利用围护结构水平位移曲线计算坑外地表沉降的简易估算方法，主要步骤如下：

(1)假设地表沉降曲线为以最大值位置水平对称的正态分布概率密度函数。

(2)基于平面应变边值条件下的地表沉降解析表达式计算地表沉降最大值位置xm。

(3)根据假设沉降曲线，结合既有经验，借助上一步所得xm计算地表沉降影响范围x0。

(4)对假设沉降函数在影响范围内进行积分运算，推导只包含未知数δmax的地表沉降曲线包络面积Av。

(5)根据围护结构水平位移实测数据，计算围护结构侧移面积Ah。

(6)根据地表沉降曲线包络面积Av与围护结构侧移面积Ah之间的相关性，计算地表沉降最大值δmax。

(7)将计算所得的δmax和相关参数代入假设函数从而估算墙后任意地表点的沉降值。

将上述方法应用于工程实例，与实测数据对比分析表明预测效果较好，验证了本文方法的工程实用性。同时，在地表沉降最大值位置xm一致的基础上，对比不同地表沉降影响范围x0计算取值方法下的地表沉降曲线，发现本文预测效果相对较好，说明根据地表沉降最大值位置xm，基于主次要影响区分界点计算地表沉降影响范围x0具有一定的合理性。此外，将本文预测方法、Hsieh等的方法与实测数据对比分析，发现利用围护结构水平位移计算地表沉降最大值位置xm与实测数据更为吻合，在基坑主要影响区内利用本文方法预测效果较好，在次要影响区利用Hsieh等的方法预测效果较好。