基于因子分析法我国物流业发展水平的实证研究

（新疆财经大学统计与数据科学学院，乌鲁木齐市，830012） 董璐璐 王合玲

1 引言

随着经济的飞速进步，科学创新技术也大大提高，各种实体产业欣欣向荣，伴随着互联网技术的大幅度提高以及交通的便利发展，人们的消费理念也随之改变，网购、电购等在线购物方式也在人民生活中普遍应用，物流业的发展也蒸蒸日上。随着物流业成为我国十大振兴产业之一后，对经济的发展起到了推进作用，政府对此也出台了相应的发展政策与规划，对物流业的发展也取得了一定的成效。基于此，科学地建立物流发展水平评价模型并进行评价，对我国的物流发展与服务水平的完善，以及经济发展具有较强的现实意义。

2 研究方法

因子分析（factor analysis，简称FA），思想源于1904 年查尔斯·斯皮尔曼（Charles Spearman）对学生成绩的研究，是主成分分析的一种推广。在研究多指标问题时常常会发现，指标相关性形成的背景原因各种各样，其中共同的原因被称之为公共因子；每个变量也含有特定的原因，称之为特殊因子。因子分析的实质就是利用几个潜在的但不能观察的互不相关的随机变量去描述许多变量之间的相关关系（or协方差关系），将众多的原有变量综合成较少的几个综合指标，这些指标被称之为因子。

2.1 因子分析的目标

因子分析的目标有：①考虑是否存在较少的不相关的随机变量可用来描述原始变量之间的关系，即因子的个数要远远小于原有变量的个数；②如果存在公共因子，那么究竟要选取几个，这就要求选取的因子能够反映原始变量的绝大部分的信息；③对提取的公共因子的含义进行解释，具有命名解释性；④评价每一个原始变量与公共因子之间的关系，且公共因子可以用于统计分析。

2.2 基本的因子分析模型

假如对某个问题的研究有关的指标有p 个，且这些指标间存在较强的相关性，则因子模型可以表示为

3 实证分析

3.1 数据的选取与模型设定

由于数据的选取性和可得性，根据全国从中国统计年鉴、中国第三产业统计年鉴以及各社会统计年报，选取了2017 年的23 个指标对中国物流业发展水平进行评价，主要考虑到物流业的基础设施、发展规模、产业结构、人力资源等物流业内部指标和描述经济发展水平以及信息化发展状况和环境影响度的外部指标来综合描述。

表1 物流业发展水平评价指标

3.2 因子分析

3.2.1 适用性检验

对变量进行KMO 检验和巴特利特（Bartlett）检验，KMO检验是通过分析变量间的简单相关系数以及偏相关系数的大小，来判断是否适合进行因子分析，通常对应的检验值越接近1 则说明适合做因子分析；Bartlett检验是用来确定拥有的数据是否来自服从多元正态分布的总体，若检验对应的统计值在显著性水平下显著，则表示选取数据符合正态分布，可以进行更进一步的分析。通过检验结果可知，描述物流业内部环境与外部环境所对应的KMO值分别为0.643 与0.736，则我们可以判断适合做因子分析；而Bartlett 球形检验对应的统计量分别为360.924 和608.977，显著性都接近于0，符合正态分布假定，相关系数矩阵与单位阵有显著差异。

3.2.2 成分提取

通过对原始变量进行因子分析，我们可以得到如下特征值及方差贡献率，通过表2和表3，我们可以发现物流业内部指标特征值大于1 的因子有3个，贡献率分别为47.141%，23.644%，15.473%，累积方差贡献率为86.258%；物流业外部指标的因子有2个，累积贡献率达到81.289%。即可以表述出原有变量的86.258%和81.289%的信息量，缺失信息较少，符合我们能反映原始变量绝大部分信息的目的，因子提取成果较好。

表2 内部指标——特征值及方差贡献率

表3 外部指标——特征值及方差贡献率

3.2.3 计算因子得分

通过表4的物流业内部与外部因子载荷矩阵可知，物流业就业人口、物流业产值、货运周转量、民用汽车拥有量、货运量在第一因子上的载荷值较高，可以命名为物流业规模因子；营运里程数、物流业从业人员占全体从业人员比例、物流业固定资产投资在第二因子上具有较高的载荷，可以命名为物流业基础设施建设因子；物流业产值占GDP比例和物流业产值占第三产业比例在第三因子上拥有较高的载荷，命名为物流业结构因子。而对于物流业外部发展水平指标，工业总产值、社会消费品零售总额、地区总产值、建筑业总产值、道路交通事故发生数、农业总产值、邮路总长度、邮电业务总量、进出口总额在第1 因子上有较高的载荷，可以命名为经济发展因子；而电话普及率、互联网用户数、人均生产总值以及工业二氧化硫排放量的因子载荷在第2因子上较高，我们命名其为信息化水平因子。

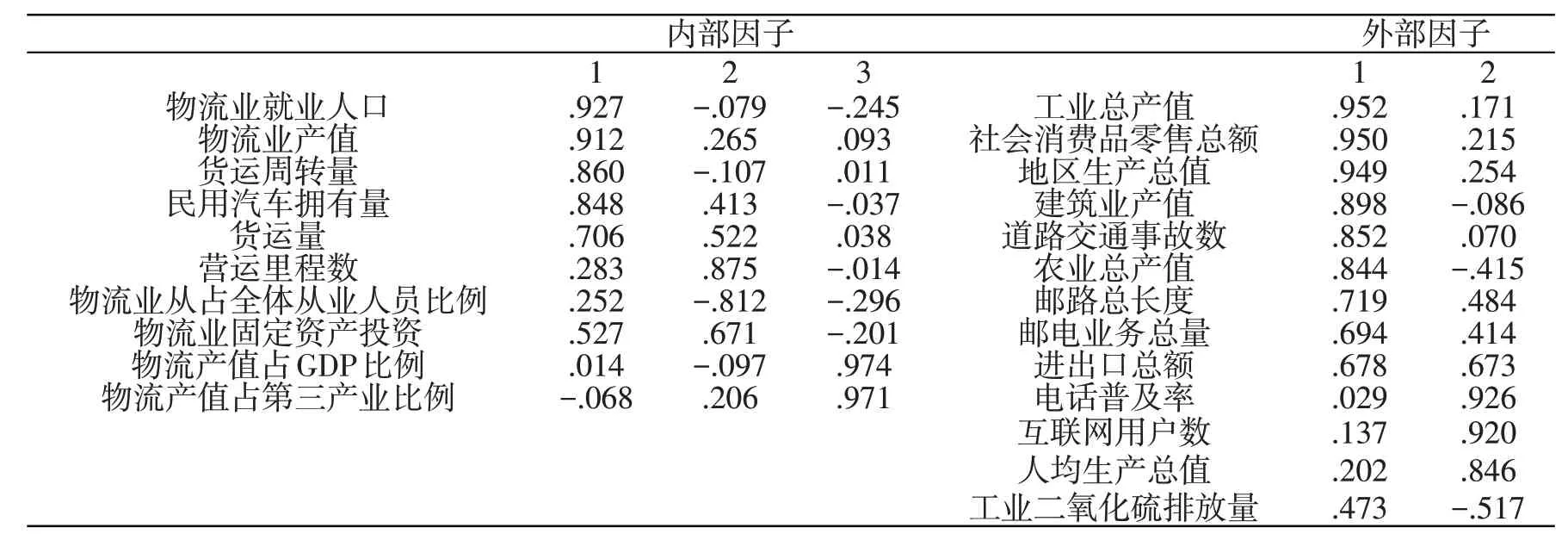
表4 物流业内部与外部因子载荷矩阵

在确定因子提取因子数后，我们通过软件操作，可以得出提取的因子的得分系数矩阵，如表5，从表中，我们可以得出公共因子的表达式：

F11=-0.047X1+0.133X2+0.186X3+0.270X4+0.268X5+0.236X6+0.087X7+0.018X8+0.174X9+0.042X10

F12=0.385X1 + 0.146X2 + 0.078X3-0.180X4-0.155X5-0.014X6-0.131X7 + 0.029X8-0.407X9 +0.265X10

F13=-0.061X1+0.025X2+0.006X3+0.075X4-0.051X5 + 0.088X6 + 0.497X7 + 0.464X8-0.062X9-0.120X10

F21=0.139Y1-0.017Y2 + 0.144Y3 + 0.161Y4 +0.150Y5 + 0.141Y6 + 0.070Y7-0.050Y8 + 0.088Y9 +0.088Y10+0.134Y11-0.032Y12+0.107Y13

F22=0.015Y1 + 0.225Y2-0.008Y3-0.166Y4-0.077Y5+0.004Y6+0.148Y7+0.257Y8+0.093Y9+0.075Y10-0.031Y11+0.249Y12-0.173Y13

利用方差贡献表的方差贡献率，可以得到我国物流业内部与外部的得分系数矩阵，根据因子得分系数矩阵确定各因子得分的基础上，计算各省物流业内部与外部因子得分，以旋转因子的方差贡献率为权重，得出物流业内部（F1）、外部（F2）发展水平综合评价模型为：

F1=（47.141×F11+23.644*F12+15.473×F13）/（47.141+23.644+15.473）

F2=（56.011 × F21 + 25.279 × F22）/（56.011 +25.279）

在物流业内部评价模型与外部评价模型的基础上，结合各指标，通过对成分矩阵、特征值以及方差贡献率的数据进行计算来确定权重，省级物流业综合发展水平的基本模型为：

F=0.42×F1+0.58×F2根据物流业内部发展水平模型、外部发展水平模型及综合发展水平模型，得到表的得分与排名。

通过因子分析法，得出了我国各省市物流能力的排名情况，从表6可以发现，广东的物流综合发展水平较高，而西藏的物流综合发展水平较差；而重庆、辽宁、山东等省虽然物流综合水平排名较前，但是物流业内部和外部发展水平不平衡；西藏、青海等省出现物流业内部发展不足，外部发展失调的情况。通过对东中西部地区的综合排名，东部地区的得分较高，排名第一，其次是中部、西部，排序结果基本上吻合，符合我国物流发展的特点，说明提取的因子具有科学性、可行性、代表性，缺失的信息较少，模型设定较为合理，评价结果接近实际。

表5 物流业内部与外部因子得分系数矩阵

表6 2017年各省物流业内、外部及综合发展水平评价得分与排名

表7 我国东、中、西部物流发展综合水平排名

4 结论

基于因子分析法，构建物流业内部发展因子和外部发展因子，包含10 个指标的物流业规模因子，物流业基础设施建设因子，物流业结构因子解释了内部发展水平的86.258%；包含13 个指标的经济发展因子，信息化水平因子解释了外部发展水平的81.289%，并建立物流业发展水平评价模型。

通过分析结果可知，我国的物流业发展存在内部、外部发展不平衡的情况，各省间的发展差异也较大，发展水平低于平均水平的省较为普遍。基于此，我国应该加强基础设施的建设，加强省域间的物流发展联动效应，优化路网交通枢纽，合理建设物流园，以便提高效率和降低成本；提高物流企业竞争力，企业间要优化结构，构建物流销售系统，物流产商集中化，实现仓储、运输、加工、装运等一体化；合理利用互联网的大数据优势，把握消费者的需求及偏好，提高市场应对力。