基于非线性动态规划的波多黎各飓风灾难救援模型研究

刘越 王志坚

摘 要：本文研究了救援响应系统开发，在装箱问题上面对客观约束采用非线性规划模型，在空间利用率达到最大化的目标函数下，对货物的数量、旋转方向、体积和承载重量做出约束，再使用动态规划模型确定装箱方案。在配送集装箱时分3种情况构造模型，分为停靠1个、2个和3个港口，遍历港口与5个医疗包交货地点间的距离并筛选得到最小距离求得对应的停靠港口。

关键词：非线性规划；动态规划；遍历

很多学者研究过三维装箱问题及最佳分配问题。本文研究的是相同尺寸物品装箱问题，通过构造模型寻找最佳包装配置，且综合考虑救援效率及成本和其他客观要求，结合实际情况为最佳包装配置选取合适港口以便进行组织的下一步营救。

1 研究背景

2017年美国波多黎各遭受当地史上最严重飓风，造成了严重破坏和重大人员伤亡。非政府组织HELP，Inc通过设计“DroneGo”可移动灾难响应系统来提高其救援响应能力。HELP，Inc已经确定使用各种旋翼无人机来组成DroneGo车队。为了增加受灾现场的援助用品，DroneGo准备了三种医疗包MED1、MED2和MED3。無人机承担运输医疗包的任务，可以通过外部货舱运输多个医疗包。本文根据各营救点的需求及救援路线和侦查路线为HELP，Inc解决营救计划的包装配置和物资运输问题。结合波多黎各的飓风灾难情景，为最多三个标准ISO集装箱设计相关的包装配置，形成HELP，Inc设计无人机队和医疗包装配方案。找到波多黎各的最佳位置，确定DroneGo灾难响应系统一个或多个集装箱位置，有利于提供医疗服务和道路视频侦察。

2 装箱问题与包装配置

无论是医疗包放进无人机外部货舱和运输集装箱，还是运输集装箱放进ISO集装箱，都要与集装箱边线平行，即正交布局。

要求最多使用三个标准ISO集装箱，本文运用非线性规划模型，把医疗包放入无人机的外部货舱，将无人机和剩余医疗包放入运输集装箱内，再把运输集装箱按数量最大限度地装载进标准ISO集装箱，即研究三维装箱问题，假设各种集装箱和医疗包的形状都是规则的长方形，它们的重心即其几何中心，对此建立空间直角坐标系。考虑目标函数和现实约束，其中需要注意的是无人机的运输集装箱只能正交旋转90°，不能对任何运输物品进行倒置或侧放。

3 集装箱停靠位置选取

装载包装配置后需要将标准ISO集装箱进行分配派送，需获取1个、2个或3个最佳停靠位置。由于最多使用3个港口，故分3种情况构造模型。

本文在GoogleMap上获取波多黎各的11个主要港口的经纬度。如下表所示：

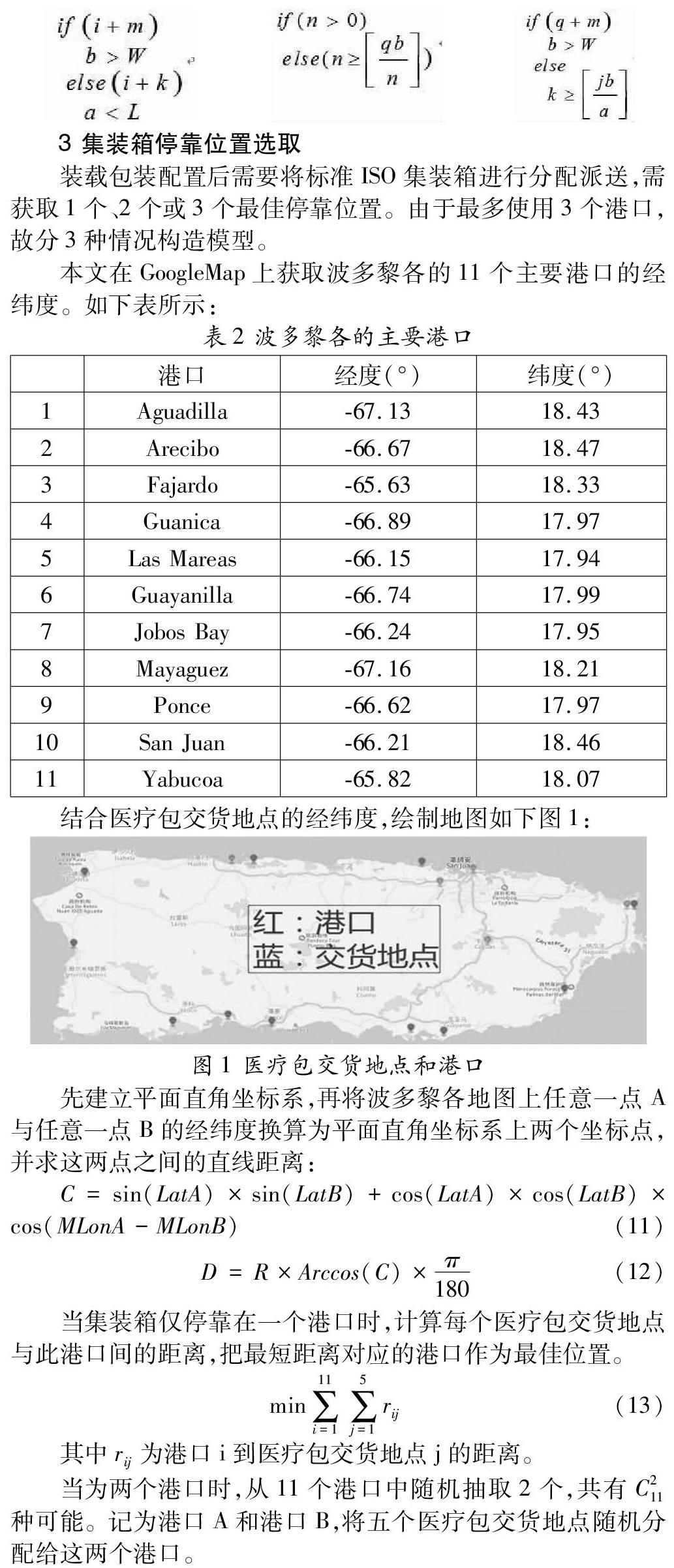
结合医疗包交货地点的经纬度，绘制地图如下图1：

先建立平面直角坐标系，再将波多黎各地图上任意一点A与任意一点B的经纬度换算为平面直角坐标系上两个坐标点，并求这两点之间的直线距离：

当集装箱仅停靠在一个港口时，计算每个医疗包交货地点与此港口间的距离，把最短距离对应的港口作为最佳位置。

当为两个港口时，从11个港口中随机抽取2个，共有C211种可能。记为港口A和港口B，将五个医疗包交货地点随机分配给这两个港口。

其中港口A分得m个医疗包交货地点，则港口B分得5-m个交货地点（m=1，2，3，4）。计算港口与所分配交货地点间的距离，求和得到分配方案总距离。通过遍历方法筛选出多种分配方案总距离最小值，把该种方案对应的两个停靠港口视为最佳停靠位置。

当标准ISO集装箱停靠三个港口时，从11个港口中任意抽取三个港口，将5个医疗包交货地点随机分配给这三个港口。同理可得多种分配方案的总距离最小值，把该种方案确定的三个停靠港口视为最佳位置。

4 研究结论

对本文非线性规划的约束条件和目标函数使用python求解，得到结果如下：

本文为灾难响应系统设置2台E型无人机，1个H Tethered平台，363个E型运输集装箱，1个H型运输集装箱和3个标准ISO集装箱。其中会出现两种装载情况，第一种情况是用无人机外部携带的货舱装载医疗包，运输集装箱装载无人机；第二种情况是仅用运输集装箱装载医疗包。再把所有运输集装箱放进ISO集装箱。

使用C++对包装配置的动态规划二维装箱模型进行装载计算，其中两个标准ISO集装箱，一个内部装载126个E型运输集装箱，空间利用率为85.1%。另一个装载111个E型运输集装箱和1个H型运输集装箱，其中有两个E型运输集装箱装载E型无人机，H型运输集装箱装载H Tethered平台，空间利用率为85%。两种装箱方案的空间利用率较高，是可行的结果。其中医疗包放进运输集装箱的方法有两种：第一种方法是3个MED1和3个MED3。第二种方法是4个MED1，2个MED2和3个MED3；且每一天所需医疗包的包装量刚好满足两个E型运输集装箱的最大承重能力，装载后的剩余运输集装箱底面面积相对较少。

在寻找最佳位置的模型中，通过python多次遍历计算得到在3种情况中港口与医疗包交货地点之间的距离，并自动筛选出之中的最短距离，其对应的港口即为标准ISO集装箱的最佳放置地点。求解得到结果如下：

参考文献：

[1]许佳瑜.三维装箱约束下的车辆路径优化研究[D].长安大学，2018.2.

[2]农健恒.同尺寸物品装箱的动态规划算法[D].广西大学，2014.

[3]郑洪清.CS算法在应急救援中最佳路径的应用研究[J].山东工业技术，2018（15）：241-242.

作者简介：刘越（1997-），广东潮阳人，2016级本科生，研究方向：应用统计学；王志坚（1982-），江西余干人，博士，讲师，研究方向：管理统计方法。