小波变换在混凝土冲击回波检测中的应用

周迪 刘昌明 王志刚 方翔

摘要：采用冲击回波法检测混凝土厚度或者缺陷时，采用传统快速傅里叶变换方法，由于傅里叶变换的时移性以及信号中包含表面波和结构模态振动使得特征频率的提取较为困难。要解决特征频率提取受到干扰的问题，该文提出一种小波变换结合傅里叶变换的信号处理方法。首先对回波信号进行小波变换，得到信号时频图和小波边际谱，其次将小波边际谱与傅里叶谱相乘，得到增强傅里叶谱。结果表明：信号时频图可以确定表面波和模态振动的频率范围和时间跨度，增强傅里叶谱不仅可保证频率分辨率，而且抑制由于傅里叶变换的时移性产生的多个波峰，使得特征频率在频谱中更为清晰和准确，是一种适用于冲击回波检测的信号处理方法。

关键词：冲击回波;傅里叶变换;小波变换;无损检测;增强傅里叶谱

中图分类号：TG115.28文献标志码：A 文章编号：1674-5124（2019）04-0135-06

0引言

冲击回波法是20世纪80年代发展起来的无损检测技术。在冲击回波测试中，使用钢球或者锤子敲击结构表面，产生包括纵波（P波）、横波（s波）、表面波（R波）等应力波，其中表面波沿表面传播，而横波和纵波称之为体波，在结构内部传播。当体波在结构内部传播中遇到声阻抗有明显差异的分界面将发生反射现象，返回到构件表面引起表面振动。应力波在结构表面和声阻抗分界面来回传播，置于冲击点附近的传感器接收到结构表面的振动。记录接收到的信号，通过快速傅里叶变换（FFT）得到频谱图，从频谱图可以得到结构的厚度和缺陷的频率信息。在激发的应力波中纵波传播速度最快，引起结构表面的振幅最大，因此，冲击回波法利用的主要是纵波。冲击回波法原理如图1所示。由于接收到的信号包含表面波、反射和衍射的体波以及结构的振动，而且傅里叶变换是建立在平稳信号的基础上，然而结构的冲击响应并不是平稳的，这些会使得频谱复杂化，特征频率的提取变得困难。

为了解决上述问题，聂文龙使用最大熵谱分析方法（MEM）分析回波信号，得出MEM分析方法的精确度、分辨率比FFT分析方法高的结论，但是MEM无法识别出表面波和结构的振动信息。苏航提出使用短时傅里叶变换分析回波信号，该方法由于受到时间窗的限制，其时间分辨率较差。陈敏、徐志胜通过小波变换对回波信号的奇异性进行检测分析，能有效消除噪声干扰，然而小波变换的频率分辨率不如傅里叶变换。在结构的振动识别方面，罗光坤和张令弥利用小波变换的模态参数识别技术识别出系统的频率、阻尼比和振型等模态参数。陈长河和陈征宙通过小波变换的多尺度频谱分解，可以清晰获得检测信号在不同频段频谱特征，研究未灌浆锚孔的信号畸变特征。桑松和柴玉华利用小波变换和傅里叶变换相结合的算法对电力系统中的谐波问题进行分析，既能检测瞬态信号又能精确地定位各次谐波，并且可以同时获谐波在时域和频域上的完整信息。

因此，在分析现有方法的基础上，提出运用小波变换识别回波信号中表面波和模态振动的频率范围和时间跨度，将小波边际谱与傅里叶谱相乘，抑制傅立叶谱中的多个波峰，使得信号的特征频率更加明显。

1信号处理

1.1傅里叶变换

2数值模拟

本研究采用数值仿真的方法模拟混凝土试件受到钢球撞击的响应。同时也用数值仿真的方法进行模态分析，以此确定结构的模态振动。

数值模拟使用具有内部裂缝的混凝土试件。其密度为2300kg/m³，杨氏模量为33.1GPa，泊松比为0.2。根据式（2）可计算出混凝土试件的纵波速度约为4000m/s。数值模拟的结构尺寸为800mmx800mmx200mm，结构中设置一320mmx320mm～10mm的内部裂缝，位于表面下120mm处。在冲击点施加近似为半周期正弦函数的变压力以模拟钢球的冲击，接触时间为te=40us。模拟中使用三维实体元素，网格设置为10-mm的六面体网格，接收器设置为距离冲击点40mm处。总模拟时间为3.072ms，时间增量设置为1us。

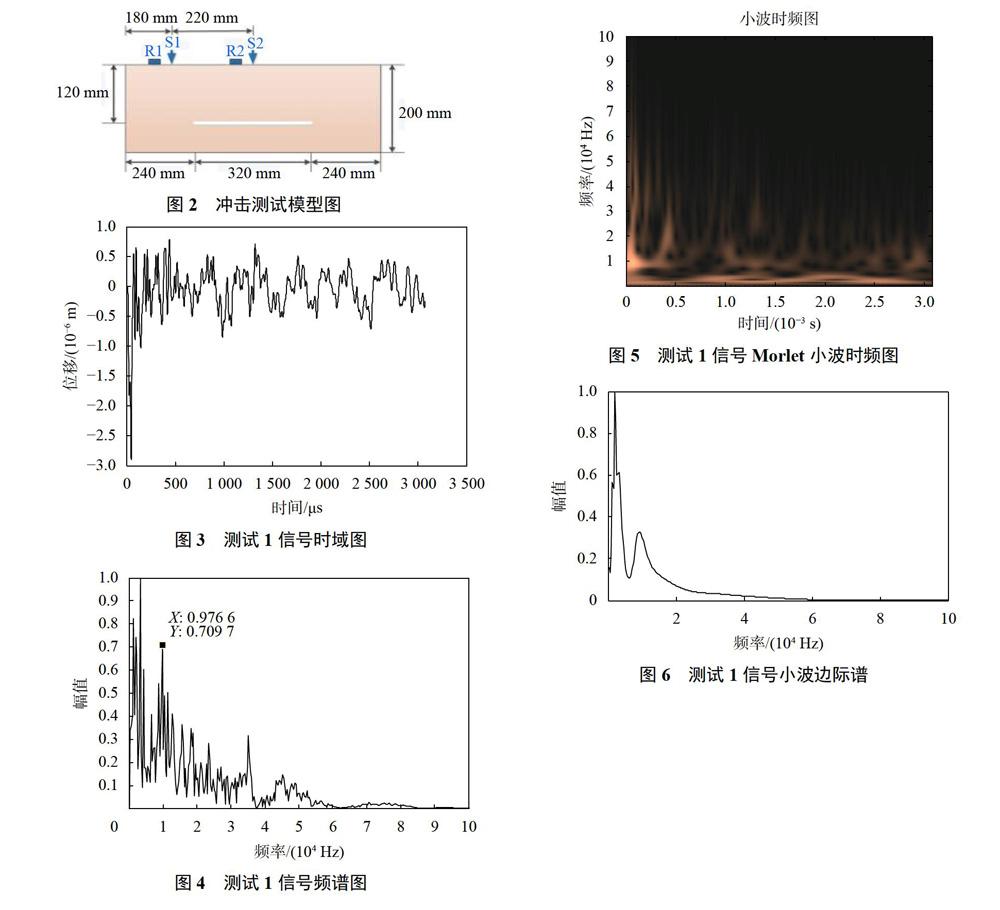
如图2所示，测试1冲击模拟中，冲击点设置在距离结构边缘180mm，测试2冲击模拟中，冲击点设置在距离结构边缘400mm处，接收点设置为距离冲击点40mm处。sl和s2分别为冲击点，R1和R2分别为接收点。

2.1测试1信号处理

图3为信号时域图，信号开始阶段包含表面波。图4为信号的傅里叶频谱图，根据式（1），虽然可以找到与结构厚度所对应的特征频率，但是在傅里叶频谱图中包含比特征频率能量大的峰值频率和由于傅里叶变换自身的时移特性造成多个波峰，同时也包含横波、表面波对频谱图的影响，使得傅里叶频谱图复杂化，特征频率变得难以提取。

通过对信号进行Morlet小波变换，以获取信号的时频谱和小波边际谱。如图5和图6所示。图5中在频率轴的开始阶段有一个水平的亮带，与图3傅里叶谱和图6小波边际谱中前段较大的幅值的波峰相对应。通过分析结构的模态，可知该频带对应于结构的模态振动。在图5时间轴的开始阶段，存在一个很长的竖直亮带，根据图3可知，这个亮带对应的是信号的表面波。

根据式（1），该处测试的特征频率为10kHz左右，图5的10kHz处存在一个水平的亮带，该亮带横跨时频图的整个时间轴，显然是由于结构模型的顶面和底面之间的多次反射造成的。

综上所述，Morlet小波变换应用于冲击回波测试中，相对于傅里叶变换的优点在于可以分辨出信号中固有频率、表面波和特征频率所对应的时间跨度和频率成分。由于小波边际谱的频率分辨率不如傅里叶变换，故通过小波边际谱确定波峰具体数值相对模糊，为了提取准确的特征频率，通过式（12）结合小波边际谱和傅里叶频谱得到增强傅里叶谱。

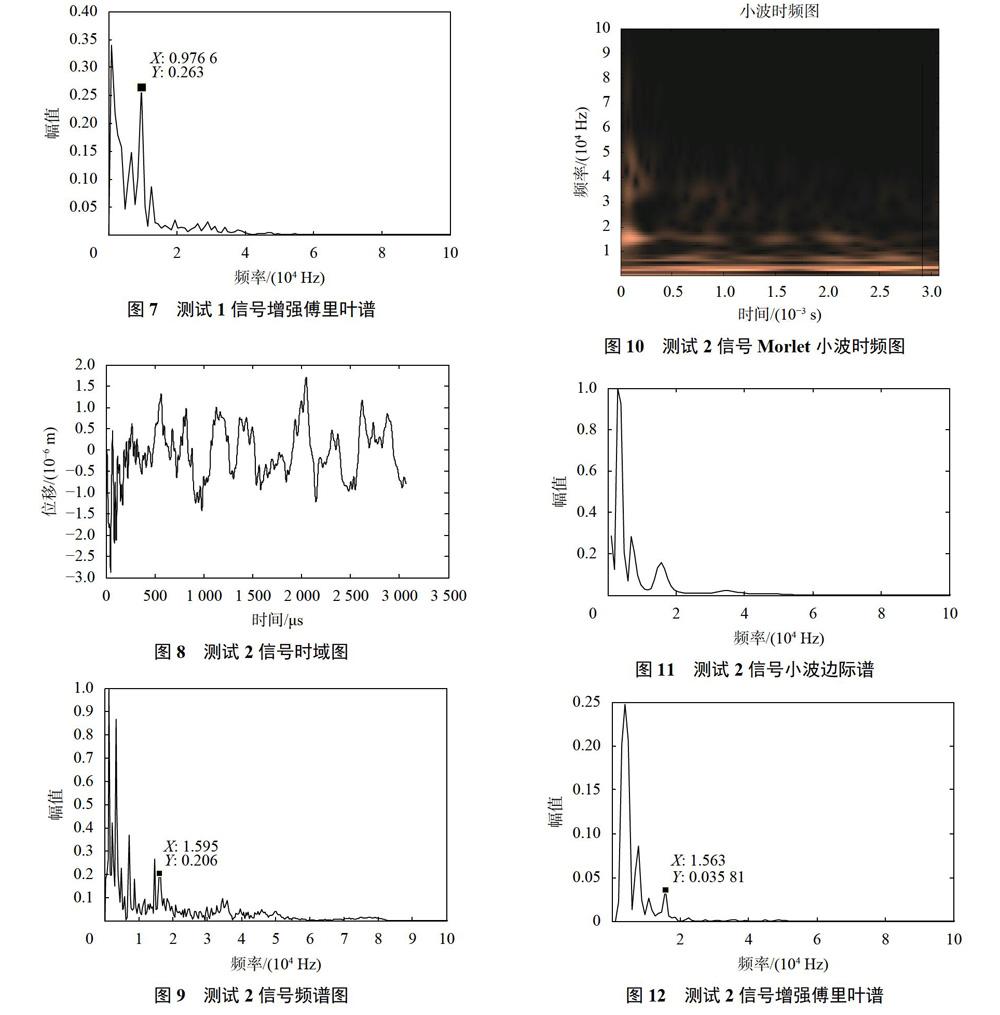
图7中所包含的波峰明显减少，说明多数干扰得以抑制。结构的模态振动频率和结构底部深度所对应的特征频率在图谱中可以清晰的提取。其中第一个波峰的频率为1953Hz，非常接近通过模态分析获得的结构模型的固有频率，因此，其对应的是结构的模态振动。第二个峰值位于9766Hz，通过式（1）得出底部深度为197.2mm，基本与结构模型相符。

2.2测试2信号处理

与测试1类似，测试2信号时域图的开始阶段也包含表面波，如图8所示。图9为测试信号的傅里叶频谱图，相比于图4其特征频率受到的干扰更大，更难明确该波峰的位置。

对测试2的信号作Morlet小波变换得到如图10所示的时频图。时频图中时间轴开始阶段的竖直亮带为表面波的频率范围和时间跨度。两个横跨整个时间轴的水平亮带与模态分析的结果相对比，其频带对应于结构的两种振动模态。在频率约为16kHz处存在一个水平的亮带，该亮带的产生由于在冲击点下方有裂纹的存在。

图11为测试2信号的小波边际谱，通过比较其波峰，可以看出随着频率的增加，波峰变得平滑。在时频图中亮带的宽度随着频率增加而变宽。这两种现象都说明了小波变换的特性，即频率分辨率随着频率的增加而降低。因此在特征频率较大的情况下将傅里叶频谱和小波边际谱相结合是一种有效的方法。

与测试1类似，图12信号的增强傅里叶谱中，傅里叶频谱中存在的多波峰和杂波的干扰在增强傅里叶谱的频谱中抑制效果明显，同时由于小波变换自身的缺点产生的高频段波峰平滑的现象也得以改善。图谱中的波峰清晰，数值容易识别，前两个波峰的频率为2930Hz和6836Hz，对应结构的模態振动。第三个波峰则是由裂纹回波产生的频率15630Hz。通过式1得出裂纹深度为122.8mm，与预设缺陷的深度基本一致。

3结束语

本文通过数值模拟的方式产生冲击回波信号，将小波变换应用于冲击回波信号的处理中，通过对比傅里叶变换和小波变换的优劣，总结出一种更好的处理方式。

1）小波变换后的小波时频图中，可以通过图中提取的信息确定信号中各种成分的持续时间和频率内容。

2）小波边际谱与傅里叶谱类似，但不包含多个峰值的影响。在小波边际谱的高频部分，由于其自身特性，频率分辨率不如傅里叶变换。

3）利用傅里叶频谱和小波边际谱的乘积获得的增强傅里叶谱不仅保证了频率分辨率，而且抑制了由于傅里叶变换的时移性产生的多个波峰，使得特征频率在频谱中更为清晰和准确，是一种适用于冲击回波检测的信号处理方法。