基于对率回归的导航信号捕获中的峰值检测方法
贾彬彬 刘俊莹


摘要:捕获是卫星导航接收机中信号处理的第一步,对接收机的各项指标如灵敏度、动态性能等有重要影响。捕获算法中最重要的环节之一是判断是否已捕获到信号,在并行捕获算法中是通过对并行相关结果进行峰值检测实现的。结合机器学习技术,将峰值检测看作是对相关结果的二分类问题。首先,在MATLAB中重复运行并行捕获算法得到包含足够数量的相关结果组成样例集;然后,使用二分类学习算法对率回归从样例集中学得一个二分类学习器,并对分类器的性能进行分析,分析结果表明了方法的可行性和正确性;最后,指出了该方法需继续研究完善的地方,为后续工程实现该方法奠定了基础。
关键词:机器学习;卫星导航;捕获;峰值检测;对率回归
中图分类号:TN967.1
文献标识码:A
捕获是卫星导航接收机[1]中实现伪码同步进而解析电文的关键步骤之一,目前已有大量并行捕获算法提出[2,3]。无论哪种并行捕获算法,最终均需要对相关结果进行峰值检测,判断是否成功捕获到信号。峰值检测一般采用门限判决的方式实现,具体分为固定门限和自适应门限两种。鉴于接收机接收到的导航信号是动态变化的,固定门限方式已不多见;自适应门限一般采用恒虚警检测方法[4],但该方法需要估计噪声功率;为降低噪声功率估计误差的影响,一些改进算法[5,6]陆续被提出,但仍属于门限判决方式。
若从机器学习[7]的角度来重新审视峰值检测,可以将这个过程看成是经典的二分类(binary clas-sification)问题,即并行相关结果是一个一维向量,峰值检测就是要根据这个一维向量“预测”是否捕获到了导航信号。因此,可以先得到一个包含了很多已知是否捕获到导航信号的相关结果组成训练集,在此训练集上训练一个二分类学习器,然后用该学习器去判断新的相关结果中是否捕获到了导航信号。
第1节对整个方法进行总述,将方法概括为两个步骤(生成样例集和训练学习器);第2节和第3节分别详细说明了两个步骤的实现细节;第4节对全文进行了总结,并指出了后续的工作。提出的方法是卫星导航信号捕获[1]与机器学习[7]两个研究方向的交叉,更详细的有关捕获和机器学习的内容参见有关文献,仅重点阐述所提出方法的实现细节。
1 研究框架
基于机器学习的方法对导航信号并行捕获相关结果进行峰值检测分为两个步骤:一是生成样例集(example set),用于后续训练并测试学习器(leamer);二是将样例集分为训练集(training set)和测试集(test set),在训练集上训练一个二分类学习器,并在测试集上测试学习器的精度(或错误率)等指标。
(1)生成样例集(见第2节)
首先,生成不同载噪比、不同起始码相位的导航中频信号(暂不考虑多普勒),例如生成GPS L1的1号星的信号,用于后续捕获算法使用;
其次,使用基于FFT的伪码相位并行捕获算法对中频信号进行捕获,相干积分时间取为1 ms,由于不存在多普勒的影响,因此当本地伪码亦选为GPS L1的1号星时,不管起始码相位如何,只要载噪比足够高,就可以捕获到卫星信号,反之则不能捕获到卫星信号;
最后,将每次捕获的并行相关结果及捕获是否成功标记缓存,即为一个“样例”(example);重复以上三个步骤,直到得到足够数量的样例组成样例集。
(2)训练学习器(见第3节)
将生成的样例集分为训練集和测试集,在训练集上学习得到一个二分类学习器,并在测试集上测试学习器的性能。
机器学习常用的分类算法[7]包括对率回归(lo-gistic regression)、决策树(Decision Tree,DT)、神经网络( Neural Network,NN)、支持向量机(SupportVector Machine,SVM)、k近邻(k-nearest neighbor,kNN)、朴素贝叶斯分类器(naive Bayes classifier)等。本文选用对率回归模型,主要原因是对率回归是一种急切学习( eager learning)方法,预测过程较为简单,便于后续硬件实现;并且经测试发现其泛化能力亦满足需要;这也符合“奥卡姆剃刀”(Oc-cam's razor)原则。
2 生成样例集
样例集的质量与规模直接影响训练出的学习器的性能。样例集的每个样例包括捕获相关结果(即,示例或样本)和是否捕获到卫星信号(即,标记)。生成样例集可分为三个步骤:生成卫星中频信号、对卫星信号进行捕获、缓存样例数据。
2.1 生成卫星中频信号
为了模拟真实的导航卫星信号,本文产生的卫星中频信号参数如下:系统采样频率fs= 62 MHz、中频频率fIF=8 MHz、量化位数8bit,载噪比以均匀分布在区间41~45dB-Hz选取、起始码片随机选取,信号长度T=2 ms(满足后面捕获需求即可),不考虑多普勒效应。以GPS L1为例来说明。
导航卫星信号包括载波、伪码、数据码(即,导航电文)三部分。为了得到导航卫星中频信号,首先,分别生成中频载波(采样频率为62 MHz,中频频率为8 MHz,时长2ms)、生成所需卫星号的伪码(起始码片随机选取,码速率为1.023 Mcps,以62MHz进行采样,时长2 ms)、生成数据码(数据速率为50 bps,以62 MHz进行采样,时长2 ms);然后将载波、伪码、导航电文三者相乘,即可得到无噪声的导航卫星中频信号;最后根据载噪比对信号加入噪声,并根据量化位数进行量化。如图1所示:
有四点说明如下:①载噪比之所以选取41~45dB-Hz,是根据后面的捕获算法确定的,在最低4ldB-Hz时,若包括正在搜索捕获的信号,刚好可以从捕获相关结果中找出峰值;②信号长度取2ms是由于后面捕获算法进行了1 ms的相干积分和两次非相干积分,刚好需要2 ms数据;③载噪比和起始码相位两个参数的变化保证信号的多样性进而保证数据集的多样性;④之所以不考虑多普勒效应,是因为它主要影响相关结果峰值的大小,在一定的多普勒频率范围内,这可以通过在捕获时用更长的相干积分和非相干积分时间补偿,为了简化中频信号生成过程,所以取消了多普勒影响,从而减小捕获同一载噪比的信号所需的相干积分和非相干积分时间,进而减小所需生成的信号长度,降低算法的时间开销。
2.2 对卫星信号进行捕获
基于FFT的伪码相位并行捕获算法是伪码并行一载波串行搜索的代表算法。该算法一次性可以搜索多个码相位,捕获速度快,占用资源相对合理。
算法流程如图2所示。首先对中频信号乘以本地载波fLO=8 MHz进行下变频,并缓存1 ms(相干积分时长),同时产生本地伪码并缓存1 ms;然后分别对缓存的结果进行FFT,再将本地伪码的FFT结果取共轭与下变频信号的FFT结果相乘,此即为相干积分结果;最后对相干积分结果取模值平方,进行若干次非相干积分(或称为非相干累加),此即为最终相关结果。
有两点说明如下:①非相干累加次数取为2次,仅为了模拟实际捕获算法实现过程,虽然可以通过增加非相干累加次数来提高捕获灵敏度,但此处仅是为了得到相关结果而己,只要信号载噪比与之相匹配、保证可以捕获到信号即可;②由于采样频率为62 MHz,因此Ims包含62 000个采样点,计算开销较大,在实际实现时对缓存结果进行了均匀抽样,仅保留了4 096点。
2.3 缓存样例数据
相关结果是一个4 096点的向量,若要直接全部缓存作为样例集示例,即每个示例有4 096个属性。属性越多学习起来越困难、模型复杂度越高,同时根据计算学习理论可知需要的样例个数越多。而从捕获峰值检测的本质来看,实际上只需要比较相关结果的最大值与噪声估计的相对关系即可。因此,本文在缓存样例集数据时所缓存的数据仅为以相关结果最大值为中心,左右各取50个值组成的101点的向量。
对于样例集的标记信息,按如下方法给定:由于相关积分结果为Ims(等于伪码周期),当捕获算法产生的本地伪码与卫星信号相同时,只要载噪比足够大(已在实际实现时保证),理论上一定可以捕获到信号,即相关结果一定存在峰值,记为正例样例;反之,记为反例样例。
在实际实现时,正例样例标记(label)记为1,反例样例标记记为0。共生成了2000个正例和2000个反例,并且将4000个样例进行了随机排序。
3 训练学习器
首先,将前面生成的样例集分为训练集和测试集,然后在训练集上使用对率回归进行学习,最后在测试集上测试所得学习器的性能。
3.1 样例集划分
为了在样例集上训练获得一个学习器并对学习器的泛化能力进行评估,本文将样例集按3:1比例划分为训练集和测试集,即大小为4000的样例集,其中3000个样例划为训练集,1000个样例划为测试集。
3.2 训练学习器
把训练集用(X3000×101,y300O×1)表示,为了使学到的分类器不是一个恒定通过原点的超平面,对训练集的示例均增加一个常数1,即训练集变为(X300O×102,y3000×1),其中X3000×102的第1列均为1。
3.3 学习器性能分析
完成学习过程后,可得学习器在训练集上的训练误差( training error)为1.43%,在测试集上的泛化误差( generalization error)为2.10%。
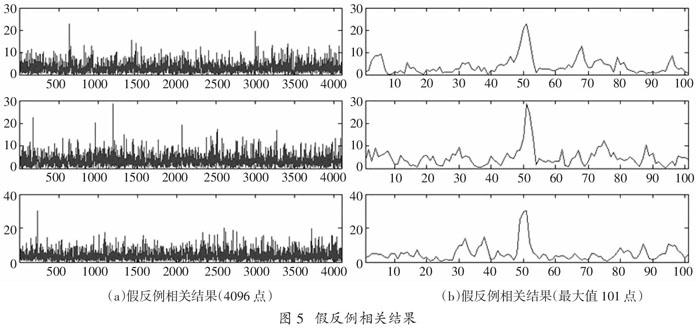
接下来分析学习器预测出错的样例,以揭示训练误差和泛化误差存在的本质原因和必然性。如图4和图5所示,分别包括随机选取的三例假正例和三例假反例相关结果,图4(a)图为误判为正例的4096点相关结果,(b)图为训练集中使用的以最大值为中心左右各取50个点的相关结果;图5 (a)图为误判为反例的4 096点相关结果,(b)图为训练集中使用的以最大值为中心左右各取50个点的相关结果。表1给出了图4和图5中的六个样例的假设函数hθ(x)的输出。
作为对比,图6和图7分别给出了随机选取的三例真正例和三例真反例相关结果,表2给出了对应的假设函数输出。
通过分析图4(b)可以发现,误判为正例的样例峰值(最大值)确实很明显,而且除峰值外的其它数据(一般称为噪底)均较小,可以与图6(b)真正例结果对比以获得直观的概念;而通过分析图5(b)可以发现,误判为反例的样例噪底比较大,可以与图7(b)真反例结果对比以获得直观的概念。相比于图6(a),可以发现图5(a)原本的三个正例均无明显峰值;相比于图7(a),可以发现图4(a)原本三个反例确实有峰值出现。对比表1和表2,可以发现误判样例假设函数输出均在0.5临界值附近。
通过以上对比预测正确的样例与预测出错的样例,可以理解图4和图5中的六个样例预测出错的必然性,即使采用一些其它的峰值检测方法甚至由专家去预测也无法避免误判。捕获算法中,经峰值检测确认捕获到信号后,会继续经过唐检测器[8]进行多次确认。本方法假设函数输出的概率可直接用于改进唐检测器:当假设函数输出接近1(如大于0.8)或接近0(如小于0.2)时,可以直接判定捕获结果,而不必经唐检测器反复验证;而当概率值接近0.5时,再由唐检测器进行多次验证以防止出现虚警和漏检的情况。
4 结论
将机器学习的分类技术应用于导航信号捕获中的峰值检测,分为生成样例集和训练学习器两大步骤。以GPS L1信号为例,说明了方法的实现过程,通过分析最终所得学习器的性能,验证了方法的可行性。由于导航信号是扩频体制,因此在扩频通信的其它应用场景,如星间链路、航天测控、移动通信等场景的扩频信号捕获过程均可以应用该方法。本方法通过从大量样例中训练得到一个预测模型,相比于传统的门限判决方式不需要估计噪声功率,在节约计算开销的同时也会更加鲁棒。
提出的方法主要在MATLAB中实现,仅为了验证方法的可行性。若要将此方法应用于实际工程应用,还有以下问题有待研究:
(1)导航接收机捕获多在现场可编程门阵列( Field Programmable Gate Array,FPGA)中实现,此时会有较大的有限字长效应[9],会影响学习器的泛化能力。定量研究有限字长效应的影响并实现泛化能力良好的峰值检测模块是后续工作之一。
(2)為了降低示例属性的冗余,直接截取以相关结果最大值为中心,左右各取50个点共101个数据作为一个示例,此数值是否有最优值仍有待研究,也就是说在学习器能取得较好的泛化能力的前提下,取尽可能少的数据个数,这既有利于减小训练开销,又有利于该方法的工程实现,尤其是有限字长效应较为严重的FPGA实现场景。
(3)该方法目前是作为一个黑盒模型使用的,其背后的具体机理有待研究,例如该方法与传统的峰值检测方法(门限判决方式)的关系;另外,由不同并行捕获算法或同一捕获算法不同参数得到的样例集训练出的不同学习器之间的关系也有待研究。
参考文献
[1]谢钢_GPS原理与接收机设计[M].北京:电子工业出版社,2009.
[2]曾婵,李卫民,毕波,高动态CPS信号粗捕和精捕算法仿真实现[J].北京航空航天大学学报,2017,43(4):790-799.
[3]韩航程,刘井龙,梁丹丹,等,基于FFT的高数据率低信噪比下的长码直捕算法[J].北京理工大学学报,2016,36(9):976- 982.
[4]熊竹林,安建平.一种低复杂度的低信噪比非相干直扩信号捕获算法[J].电子学报,2016,44(4):753-760.
[5]尚耀波,郭英,王锦江,等,基于信噪比的自适应门限判决PN码捕获算法[J].南京邮电大学学报:自然科学版,2014,34(4): 88-93.
[6]杜洋,董彬虹,党冠斌,等.采用多相关峰值的PN码频域匹配滤波捕获实现方法[J].信号处理,2016,32( 9):1087-1092.
[7]周志华,机器学习[M].北京:清华大学出版社,2016.
[8]朱云龙,丑武胜,杨东凯.Tong检测算法性能分析及参数设置[J].北京航空航天大学学报,2015,41( 3): 418-423.
[9]黄磊,张其善,寇艳红.GPS信号FFT捕获算法的有限字长效应分析[J]宇航学报,2006,27(5 ):1029-1033.

