流形正则化框架下的极限学习机预测锂电池SOC方法
谈发明,李秋烨,赵俊杰,王 琪
(江苏理工学院 a.信息中心;b.电气信息工程学院,江苏 常州 213001)
0 引 言
锂电池管理系统优化控制的前提条件是要获得电池荷电状态(State of Charge,SOC)的精确值。根据当前的SOC值来估计锂电池续航能力,以防锂电池在使用过程中放电过度造成电池损害而导致危险情况发生。因此,如何精确预测锂电池的SOC成为锂电池管理系统的重点研究问题。
Huang等提出了基于单隐层前馈神经网络的一种极限学习机(Extreme Learning Machine,ELM)学习算法,该算法随机产生隐层输入权值和偏置,整个过程一次完成,学习效率高,被广泛应用于SOC预测所属的回归领域。文献[1]中利用ELM针对磷酸铁锂电池建模预测SOC取得了较好的效果,并验证了预测性能超越了神经网络和支持向量机方法。文献[2-4]中采用不同的启发式搜索算法对ELM的输入权值矩阵和隐层偏置量进行寻优,降低了随机性给ELM带来的影响,SOC预测精度较ELM直接建模有所提高。文献[5-6]中为了提高ELM建立的SOC预测模型的拟合和泛化能力,采用贝叶斯方法优化ELM的输出层权重,实验结果验证了其预测电池SOC方面应用的有效性。文献[7]中提出基于核的ELM在线预测电池SOC,无需事先确定隐层网络节点数量,使网络输出权值随新样本逐次加入递推求解更新,提高了预测模型的泛化能力和在线学习效率。以上几种方法中,ELM均基于经验风险最小化原理,在锂电池SOC建模预测实际应用时还是可能出现过度拟合问题。
本文提出了一种流形正则化框架下的极限学习机(Manifold Regularization Extreme Learning Machine,MRELM)建模预测锂电池SOC的方法。首先,为了提高建立预测模型的泛化性能,克服ELM采用最小二乘法求解输出层权值,随机初始化隐层节点偏置与输入层权值所导致的潜在过拟合问题,在流形正则化框架内针对极限学习机进行泛化性能方面的优化;其次,由于引入了流行正则化方法,导致存在正则化参数存在如何寻优的问题,通过差分进化(Differential Evolution,DE)优化算法寻优取得全局最优解。最后,通过采集的锂电池的端电压、电流、温度、内阻以及SOC样本数据进行实验验证,取得了很好的应用效果。
1 ELM建立预测锂电池SOC模型
对于离线采集到的任意N组锂电池训练样本数据集{(xi,yi)}i=1,2,…,N,其中:xi=[xi1,xi2,xi3,xi4]为输入训练样本的端电压、电流、温度及内阻数据;yi为标签样本的SOC数据。对于含有l个隐层节点的ELM,回归模型定义为:
(1)
式中:ωi=[ωi1,ωi2,ωi3,ωi4]T是连接输入节点和第i个隐含层节点之间的权值;bi为第i个隐层节点偏移量;g(ωi,bi,xi)为激活函数;βi为第i个隐层节点输出权值。
据此可得到根据ELM回归模型建立的电池的预测模型结构如图1所示。
将式(1)以矩阵形式表示为:
Hβ=Y
(2)
式中:Y为位置期望输出矩阵;β为输出权值矩阵;H为隐含层输出矩阵,
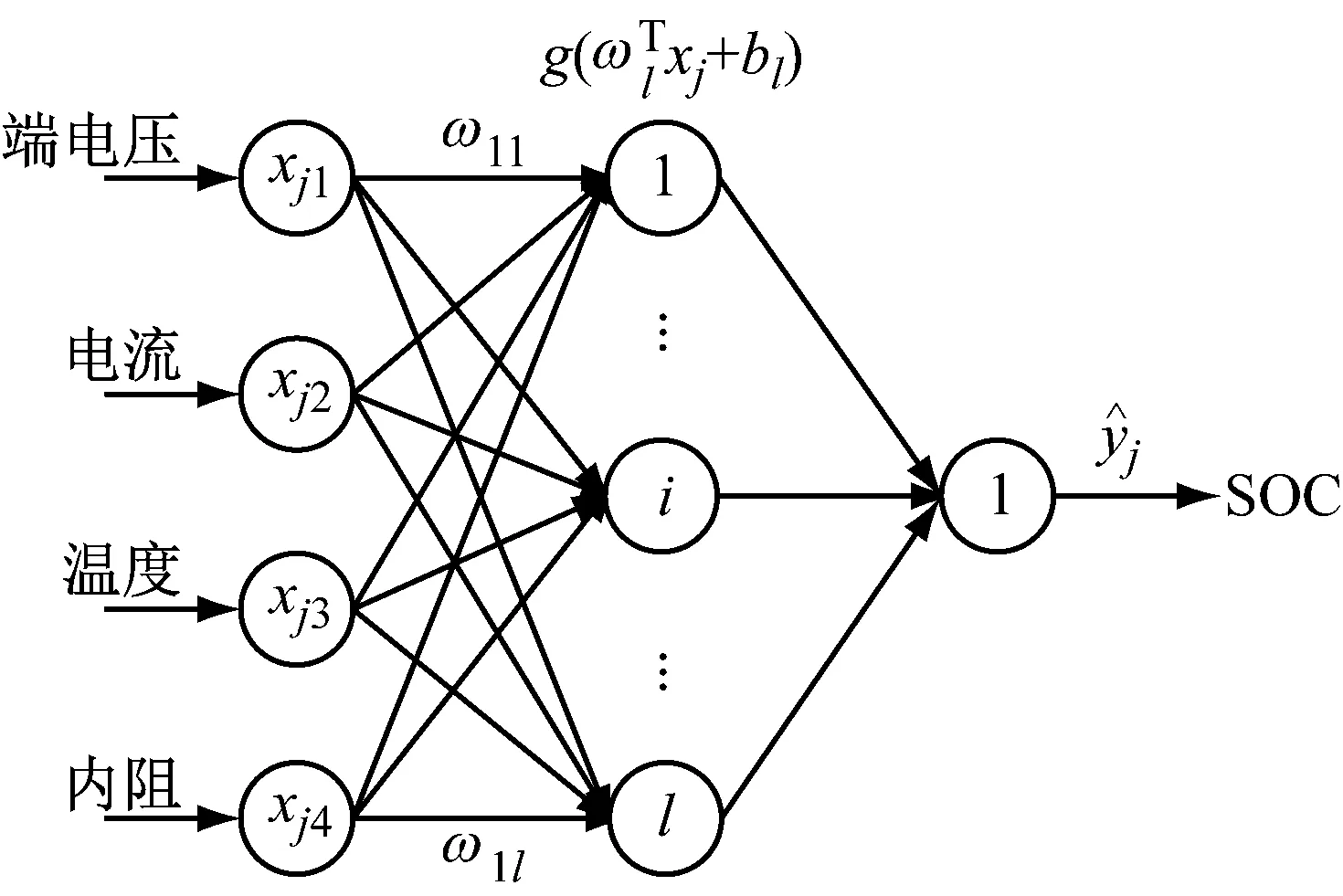
图1 ELM预测SOC模型结构
(3)
ELM学习过程关键在于计算输出层的权值矩阵β,利用最小二乘法求解式(2)可得
β=H+Y
(4)
式中,H+是矩阵H的Moore-Penrose广义逆。
使用ELM建立锂电池SOC预测模型存在以下两点问题:
(1)ELM没有能权衡好经验风险和结构风险[8],未考虑结构化风险,因此容易导致过度拟合问题,泛化性能变差;
(2)输入的锂电池数据样本在ELM特征空间中分布存在一定的随机性,无法直接用最小二乘法求解和恢复这种非线性几何结构[9]。
2 流形正则化框架分析
流形正则化使数据在新的决策空间中能够保持数据在原有特征空间中的局部几何结构,即如果某2个单样本点在原特征空间中的相似度很大,则它们在新的投影空间中的距离应该很近[10-11]。假设2个点xi和xj在相同的局部邻域,那么其条件概率P(y|xi)和P(y|xj)也应该相似。由于条件概率不便于计算,因此,本文采用数据样本的预测误差加权平方和近似,据此可定义流行正则化框架内提出的最小化成本函数:
(5)
式中:yi和yj分别是样本xi和xj的输出预测值;wij为相本点xi和xj之间的边权值矩阵,表示2个点的相似程度。采用公知的K近邻方法,即通过计算欧式距离方式找到与样本点xi距离最近的k个样本,将这k个样本定义为xi的邻居。本文引入高斯核函数计算各点与xi的相似度,该策略可以很好地反映样本空间的流形,以提高预测精度[12],具体如下式所示:
wij=
(6)
式中:ρ为宽度参数;e(xi,xj)=1表示xi和xj互为邻居关系;C(xi)=C(xj)表示xi和xj属于同一类别。通过上述方法,可得到相似度矩阵
(7)
根据流行正则化理论,最小化式(5)中的最小成本函数,即相当于最小化如下目标函数:
min:tr(YTLY)
(8)
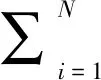
3 流形正则化框架下优化ELM
流形正则化框架下优化ELM以特征空间作为出发点,通过流形学习挖掘高维空间的数据几何结构,在ELM算法中引入流形正则化项,约束输出模型的几何形状,能有效解决模型高复杂度引起的泛化性能下降问题[13]。将式(8)引入到ELM目标函数中,则构成了流形正则框下的极限学习机学习方法,MRELM的目标函数如下所示:
(9)
式中:L是由在ELM特征空间中的样本求得;正则化参数C1用来平衡ELM的经验风验和结构风险;C2为流形正则化结构中的正则化参数,其对应目标函数中第3项的主要作用在于使ELM 特征空间中相似度较大的数据在决策空间中的距离较小,即在决策空间中保持数据在原 ELM 特征空间中的几何结构性质。将约束项代入目标函数,上式可以表示为如下形式:
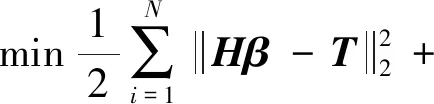
(10)
流形正则化框架下优化极限学习机不仅考虑了数据的结构特性,而且折中了经验风险和结构风险[14]。进一步对矩阵β求导为零可得:
β=(HTH+C1I+C2HTLH)+HTT
(11)
此解不但可以达到最小训练误差,同时对野值有一定的抗干扰能力,具有相当高效的泛化能力。总结MRELM算法实现步骤具体描述如下:
输入N个采集到的锂电池训练样本数据集{(xi,yi)}。
输出隐层节点的输出矩阵β。① 使用K近邻法计算单个样本与相邻相本距离,计算相似度,构建相似度矩阵W;② 计算图拉普拉斯阵L;③ 设置ELM隐层节点数,激活函数形式、极值及偏置;④ 计算隐层输出矩阵H;⑤ 计算隐层和输出层之间的权值矩阵β。
4 利用DE算法寻优MRELM正则化参数
DE算法是一种高效的全局优化算法,它是基于群体的启发式搜索算法,群中的每个个体对应一个相应的解向量[3]。利用DE算法优化MRELM模型正则化参数C1和C2,以采集的锂电池样本数据作为训练样本,具体迭代步骤如下:
步骤1初始化交叉概率CR、搜索维数D、缩放因子F以及种群数量,种群初值通过以下式子来进行初始化:
xi=xmin+rand (xmax-xmin)
(12)
式中:xmin、xmax是其某一维的取值边界;rand为(0,1)之间的随机数。
步骤2父代个体间选择两个个体进行向量做差生成差分矢量,然后,选择另外一个个体与差分矢量求和生成实验个体,完成变异操作。缩放因子F主要影响算法的全局寻优能力。F越小,算法对局部的搜索能力更好;F越大算法越能跳出局部极小点,但是收敛速度会变慢。
步骤3选择好交叉概率CR,将变异向量与目标向量进行交叉操作得到最新的实验向量ui。CR主要反映的是在交叉的过程中,子代与父代、中间变异体之间交换信息量的大小程度。CR的值越大,信息量交换的程度越大。
步骤4DE采用贪婪选择的策略,选择较优的个体作为新的个体,选择过程分2种情况:
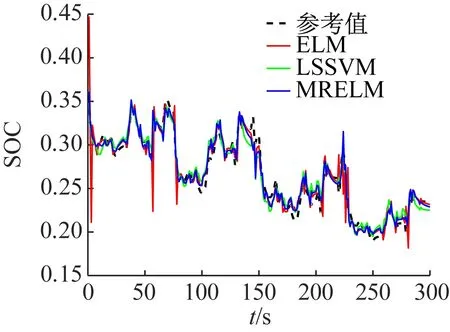
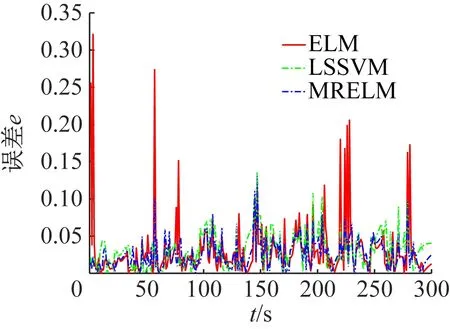
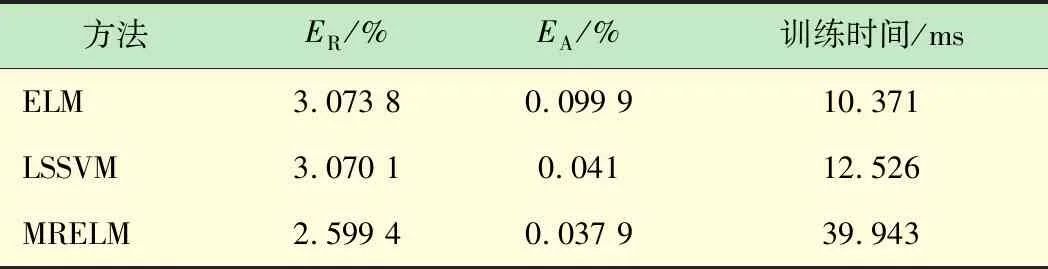
① 如果f(ui) ② 如果f(ui)>f(xi),则xi+1=xi, (13) 实验样本数据的获取采用多物理场仿真软件COMSOL对石墨/LMO锂电池采用电化学方程模型建模仿真得到。电池内部模型域构成主要为:负多孔电极采用石墨(MCMB LixC6)活性材料和电子导体;正多孔电极采用LMO(LiMn2O4)活性材料、电子导体及填料;电解质采用1.0 mol/L LiPF6 in EC:DEC(质量比为1∶1)。实验锂电池对象组件的电压约4 V,模拟测试工况为油电混动汽车驾驶循环。 以1 Hz的频率采集测试过程中锂电池的端电压、电流、温度、极化内阻及SOC数据,共获取601组样本数据,采集数据建模输入样本信息如图2所示。 (a) 电压样本(b) 电流样本 (c) 温度样本(d) 极化内阻 图2 锂电池样本数据 图2(a)为锂电池端电压;图2(b)为锂电池在测试工况条件下的样本电流数据,设定负载放电倍率为20C(1C=12 A)。由于模拟测试工况存在再生制动过程,会导致图3中的SOC变化时而呈现出增加趋势波动,对应电池电流的负值部分,符合实际应用情况;图2(c)表示电池表面温度随着电池的使用缓慢上升状态,温度的变化对锂电池内阻的影响也较大。图2(d)中的电池极化内阻变化剧烈,说明电池内部极化和浓差反应较强。由图3可知,锂电池在使用过程中SOC整体趋势呈缓慢下降态势。 图3 锂电池SOC变化曲线 从验证有效性的角度出发检验算法建立预测模型的泛化性能。在实验获得样本数据中选取奇数项数据用于训练建模;偶数项数据用于对所建预测模型的测试。系统运行软件条件为Matlab 2016b,硬件条件为Core i3二代处理器和8GB DDR3内存的台式电脑。 由于锂电池电压、电流、温度及内阻在采集时使用不同的单位,表示含义不一,在数量级上存在很大的差别,影响算法收敛速度和精度。在训练模型之前,本文采用0均值标准化方法将这些数据处理为归一化为[0,1]范围内的新数据,去掉量纲,使指标之间更具可比性[15]。 DE-MRELM算法中除正则化参数外的其他参数设置如下: (1)MRELM部分。隐层节点个数l=30,激活函数采用Sigmod函数形式,K近邻法最近邻数k=12,高斯核函数宽度参数ρ=1; (2)DE部分。种群规模N=30,搜索维数D=2,迭代次数tmax=200、交叉概率CR=0.2,缩放因子F=0.5,待寻优的正则化参数C1和C2的取值范围为[0.01,1 500]。图4进化曲线说明利用DE算法优化MRELM的正则化参数,不仅收敛速度快,而且精度高。采用这种方式寻优正则化参数的最终结果为C1=767.4及C2=1 024。 图4 目标函数值进化曲线 为了说明MRELM建立预测模型的性能优势,利用MRELM、ELM以及最小二乘支持向量机(Least Squares Support Vector Machine,LSSVM)3种方法在相同样本数据条件下建立预测模型进行测试效果比较。ELM和MRELM公共部分参数设置相同;LSSVM的核函数形式选择RBF,采用DE算法寻优LSSVM正则化参数和核函数参数,其对应值分别为0.1和99.76;3种方法的测试结果如图5所示。 图5中3种方法预测值和真实值的咬合度都比较紧密,收敛精度较高。但ELM建立的预测模型在多个测试点出现过拟合的现象,泛化性能不足。LSSVM建立的预测模型在精度方面和MRELM对比还是有所欠缺,MRELM方法在锂电池能量回馈较多的区域,仍然能够保持较强的跟踪响应速度和精度,总体性能最优。由图6可见,应用MRELM算法预测准确度最高,误差小,误差分布均匀密集。 图5 建模预测结果比较 图6 预测结果误差比较 为了进一步评价3种算法的优劣,利用训练时间和预测结果的绝对误差及相对误差作为衡量标准,绝对误差EA和相对误差ER的定义如下: (13) 误差结果如表1所示。 表1 不同方法的性能比较 从表1的性能比较结果可以看出,MRELM建立的预测模型精度最高,但训练时间稍长,其主要原因就是在于训练前需要对样本数据进行特征空间映射,建立图拉普拉斯矩阵花费了较多的时间。总体而言,应用MRELM方法建立锂电池SOC预测模型性能更加优越。 (1)分析了ELM算法建立锂电池SOC预测模型的方法,并指出其建立模型存在的缺陷。 (2)引入流形正则化框架结构优化ELM构成MRELM,并用DE算法寻优MRELM的正则化参数,能有效提高所建模型预测锂电池SOC的精度和泛化能力,给出了方法具体的实现步骤。 (3)采集锂电池的实验样本数据,利用MRELM、ELM以及LSSVM 3种方法建立预测模型进行测试比较,实验结果表示MRELM算法建立的模型性能占优,有很好的推广应用价值。
5 实验与分析
5.1 样本数据采集分析
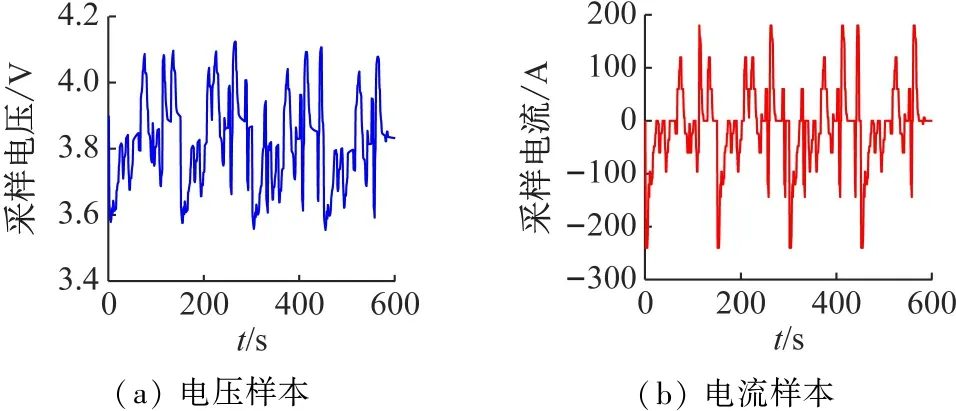
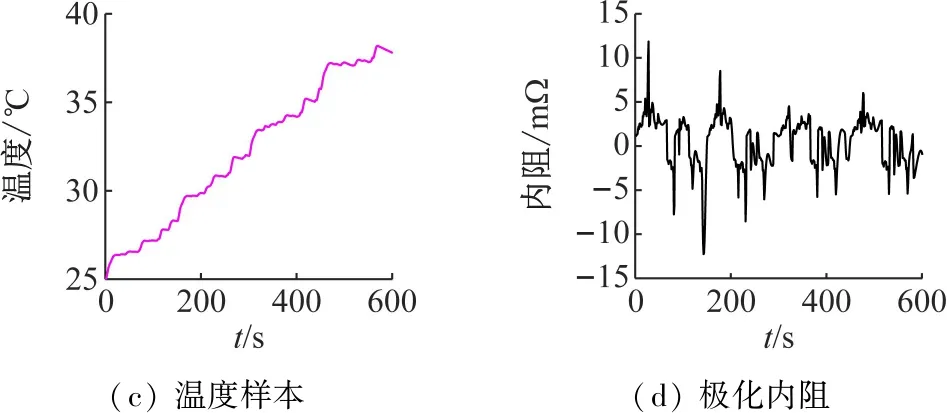
5.2 建模性能测试分析
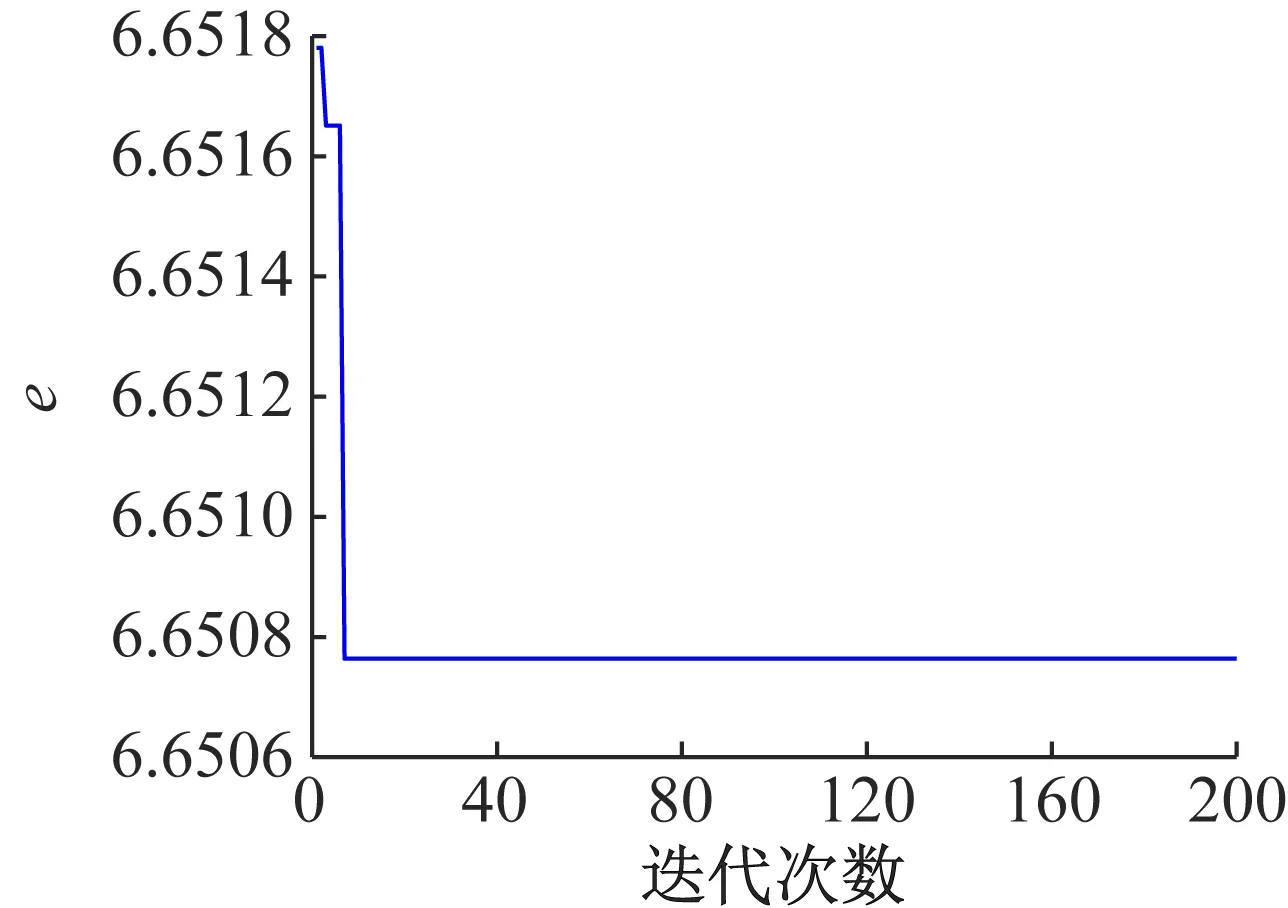
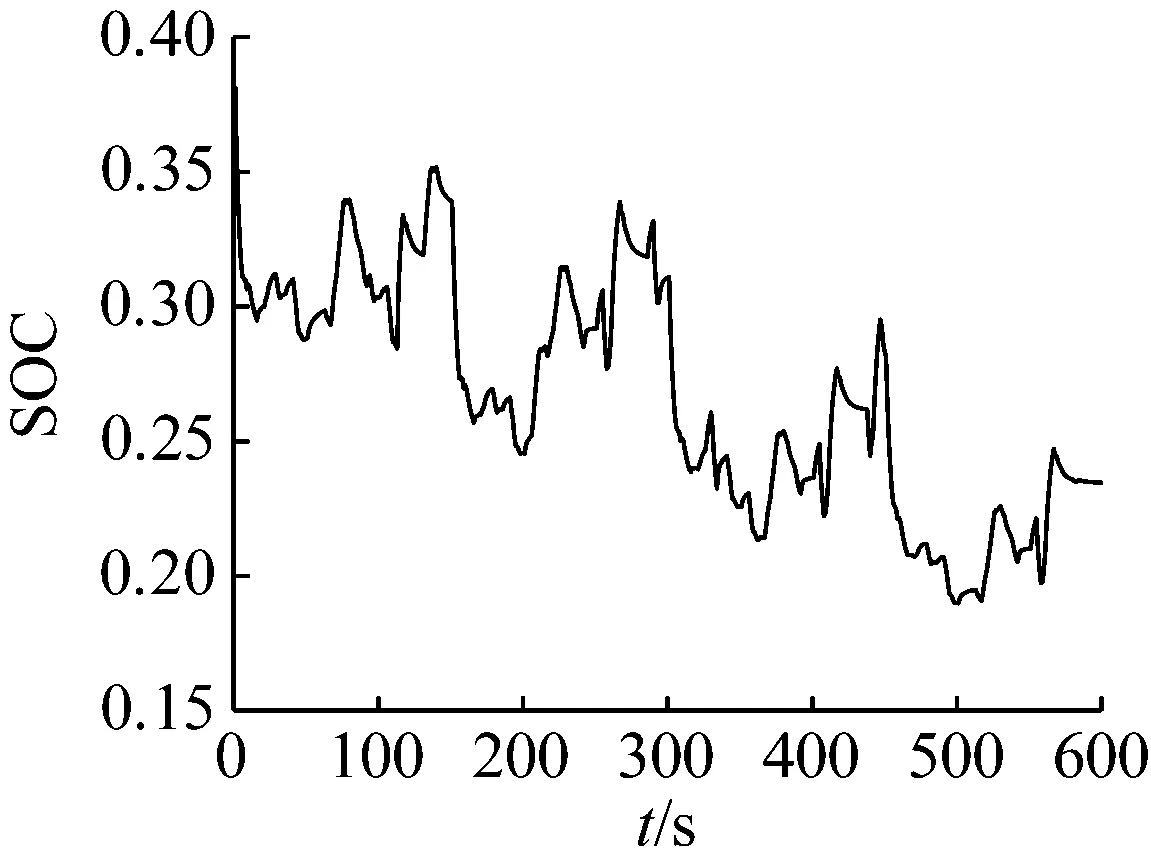
6 结 论

