一类新的基于元胞自动机的S盒的密码学性质研究

关杰，黄俊君

（解放军战略支援部队信息工程大学密码工程学院，河南 郑州 450001）

1 引言

基于元胞自动机（CA, cellular automaton）的S盒[1]因其良好的密码学性质及较低的实现成本被广泛应用到许多密码算法中，其中最典型的是已经作为SHA-3标准[2]之一的Keccak杂凑函数[3]。本文选用了一个作用域范围仅为3个元胞的局部规则，从而使该算法的S盒有着极小的软件实现成本及硬件实现消耗。目前，接触到的其他利用元胞自动机的局部规则定义S盒的密码都使用了与Keccak杂凑函数的 S盒相同的局部规则，如 Panama[4]、Subterranean[5]和 3Way[6]。除了这些 S盒外，还有一些密码算法使用的S盒是Keccak杂凑算法的S盒的仿射变换，如Ascon[7]。

本文通过实验找到了一类新的基于元胞自动机的S盒，并对这一类S盒的密码学性质进行研究，该类S盒相比Keccak杂凑函数的S盒差分性质更好，并且在输入输出规模为5时也是一个置换，因此这一类新的S盒有潜力代替Keccak杂凑函数的S盒，为密码设计者提供设计参考。

2 基本概念

2.1 S盒的密码学性质

在分组密码的设计中，最通用的设计准则就是香农提出的混乱和扩散原则[8]。在实际的设计过程中通常使用S盒来提供混乱效果，在很多密码中S盒都是唯一的非线性环节。一个m进n出的S盒可以用映射表示，其中，m、n都是正整数。

置换性质[9]和差分性质是S盒重要的密码学性质，具有良好差分性质及满足置换条件的S盒将有更广泛的应用场景。下面给出置换和差分的定义。

定义1[10]设，若对任意且，有，称F是一个置换。

定义2[11]设，那么称为F在输入差分为α，输出差分为β下的差分转移概率，其中，#{⋅}代表集合中元素的个数。

2.2 元胞自动机

元胞自动机是一种广泛应用在不同领域，用来模拟和分析复杂离散问题的并行运算模型。一个CA可以表示为一个由元胞（cell）组成的元胞空间（lattice）。在每一步状态更新中，元胞空间中的每一个元胞根据局部规则（local rule）同步更新状态。CA中所有元胞的状态从原有状态到一步更新后的状态之间的映射可以用全局规则（global rule）来表示。事实上，如果经过合理的设计及选取，全局规则可以是一个具有良好密码学性质的非线性映射，即本文要研究的基于CA的S盒。根据划分的不同，CA有很多分类，本文仅考虑一种可以用作S盒的一维布尔型循环边界CA，这种CA的定义如下。

可以把元胞空间看作是等间隔排列在直线上的一系列完全相同的元胞，且每个元胞的状态均取自集合Z2={0,1}。

设Z*为整数集合，假设元胞空间的规模为n且n∈Z*，即该CA由n个元胞组成，那么所有元胞的状态可以用一行有限的符号序列来表示，当其中每一个符号取特定状态就可以构成一个状态序列，称每个这样的状态序列为CA的一个构型。构型中的每一个元胞是用取自Z2的状态来表示的，例如构型X可以表示为，其中，

在一次状态更新中，设更新前的构型为X，那么更新后的构型完全由X决定，记为X′。其中，X′中第i个元胞x′i的状态由X的xi及其右边不超过r(r≤n-1)个元胞的状态决定，即

下面，给出一维布尔型循环边界CA的定义，如定义3所示。

定义 3[12]映射为一维布尔型循环边界 CA，其中，*n∈Z为元胞空间的规模，存在r＞0及，对 CA的任意构型，有

其中，r为CA的邻域半径，f为CA的局部规则，Fn为CA的全局规则。

图1是一维布尔型循环边界CA的示例，其元胞空间的规模n=5，局部规则可表示为，且其邻域半径r=2。可以看到，在这种循环边界的CA中，其元胞空间可以看作一个首尾相接的环，最开始的元胞接在最后一个元胞后，因此在更新最后r个元胞的状态时，会从最开始的r个元胞中选取部分作为其右邻域的一部分。在图1中，CA向量的最右侧用最开始的r=2个元胞接上，在最后2个元胞更新时可以作为其右邻域。

图1 一维布尔型循环边界CA示例

图1中的CA的局部规则就是用于Keccak的非线性变换χ，本文将该CA的局部规则记为fK，全局规则记为。

接下来，本文将给出CA的一个重要性质。本文所有运算都是在模n上进行的。

定理1CA的平移不变性。设为一个 CA，其局部规则为，其中n∈Z*,r＞0且n＞r，设为该CA的构型，令σk(X)为对X循环左移k位，那么∀X、∀k∈Zn均有

证明令，那么，所以有

故结论成立，证毕。

在一般的CA中，局部规则对第i个元胞xi的作用域为，不仅跟右邻域相关，还与左邻域相关。但是根据定理1可知，把CA的构型经过平移后可以与上文介绍的CA的局部规则一样，仅与右邻域相关而不改变其置换性质和差分性质。

2.3 一类新的基于CA的S盒

由于用全局规则就可以唯一地表示一个 CA，而一个CA经过合理地设计后，可以使全局规则成为一个密码学性质良好的非线性变换，从而可以用作密码环节中的S盒。为了找到密码学性质良好的基于CA的S盒，本文通过实验穷举了规模为5的所有CA并从中筛选出一个CA。该CA具有良好的差分性质且满足置换条件，然后本文将其在不同的规模下的情况抽象成一类CA。

下面，给出本文要研究的这一类新的基于 CA的S盒的定义。

定义 4设n≥5，映射为一类CA，其局部规则为且满足

3 的置换性质分析

置换性质是S盒一个重要的密码学性质，满足置换性质的S盒在很多密码体制中实现数据变换，具有广泛的应用场景。

引理1对于元胞空间规模n为偶数的CA，设局部规则为f(x0,x1,…,xr)且r＜n，若r为奇数，有若r为偶数，有那么该 CA的全局规则n

F必然不是一个置换。

证明设X、X*∈Z2n，如果能够找到X≠X*，使得F(X)=F(X*)，那么F不是一个置换。由于n为偶数，本文令令X*=若r为奇数，有

若r为偶数，有

显然，此处X≠X*，但有所以此时全局规则nF不是一个置换，证毕。事实上，Keccak中的非线性映射的全局规则在n为偶数时不是一个置换，因为对应的局部规则fK有，根据引理1即得。

引理 2设n≥6且n为奇数，对于，有对于

证明首先，令，令X′=那么有

当n=7时，令X=(1,1,1,1,0,0,1)，容易验证成立；当n=9时，令X=(1,1,1,1,0,0,1,0,0)，同样有0,1,1,1,1)成立；当n≥11时，令X=(1,1,1,1,0,0,1,，验证有。又因为

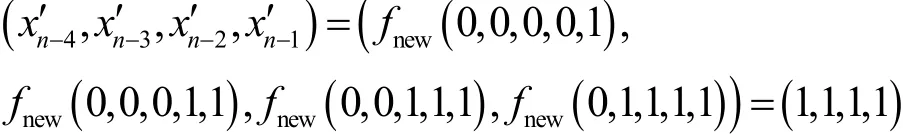
综上所述，结论成立，证毕。

定理2 设，当n=5时，是置换；当n≥6时，不是置换。

证明对于，容易验证遍历 32个输入X会有对应 32个不同的输出Y，即对于任意的，必然有Y≠Y*，所以是置换。

下面，分2种情况讨论n≥6时不是一个置换。

情况1n≥6且n为偶数，此时由得

所以根据引理1可知，当n为偶数时不是一个置换。

情况2n≥6且n为奇数，由引理2可以构造同时可以构造，也有但是，所以此时也不是一个置换。

综上所述可知，当n≥6时，均不是一个置换，证毕。

4 的差分性质分析

令n∈Z*，设，记的输入差分为，输出差分为，由于，那么输入差分和输出差分之间满足如式(1)所示的等式。

本文把n位输入差分和输出差分的关系用n个式子组成的方程组来表示，如式(2)所示。

该差分方程组对应的n维系数矩阵就是的差分矩阵，记为A，如式(3)所示。

其中，Ai(i∈{0,1,2,…,n-1})表示A的第i行。另外，A仅与的输入差分相关。

定理 3设n≥5，对于，任意输入差分及输出差分β，若差分转移概率，那么一定有其中表示A的秩。

证明设的输入，输入差分及输出差分分别为和。其中，。由式(1)可得

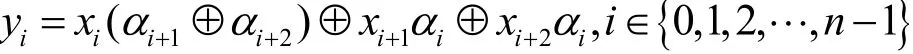
对于确定的iα及iβ，本文可以得到方程组系数的值及yi的值，所以该方程组就是Z2上的非齐次线性方程组，并且其系数矩阵即为的差分转移矩阵A。将该非齐次线性方程组用矩阵形式表示，如式(4)所示。

其中，ki∈{0,1}，ηi是方程组线性无关的基础解系，。遍历所有的ki可以得到所有方程组的解，所以解的个数为2n-r个，也就是说所以有

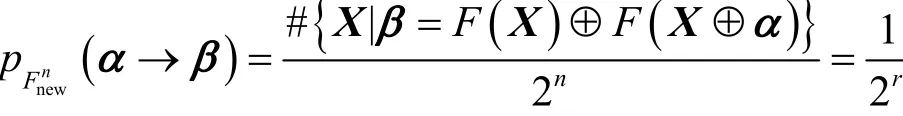
证毕。

定理4设n≥5，对于，任意输入差分α及输出差分β，若差分转移概率不为0和1，那么

证明设的输入输入 差分，输出差分β=

首先，对任意选定的α≠0及输出差分β，若存在X满足，则显然X⊕α满足此式，所以非零时必为偶数。故当差分转移概率非零时，其最小值为，所以显然成立。

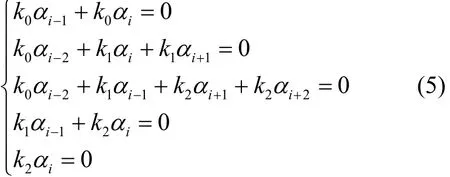
由k2αi=0可知k2=0。下面分别讨论αi-1取值为0和1这2种情况。

情形 1若αi-1=0，由得k0=0。因为k0、k1、k2不全为0，所以必有k1=1。那么由得αi+1=αi= 1，最后根据有αi-1=0。考虑，经初等变换后有

情形2若αi-1=1，由知。因为不全为0，所以必有k0=1。

经过上面讨论可知，对任意输入差分α≠0，A的秩r≥3。根据定理3，任取输出差分β，若β)≠0，则必有证毕。

5 的差分分布

定理 5设n≥5，对于，任意输入差分及输出差分，设σk(α)为对α循环左移k位，那么令若且，则

证明不妨先设k=1，对有。记在输入差分为α与α′时的差分转移矩阵分别为和那么有

在Z2上对其进行初等变换可以转化为

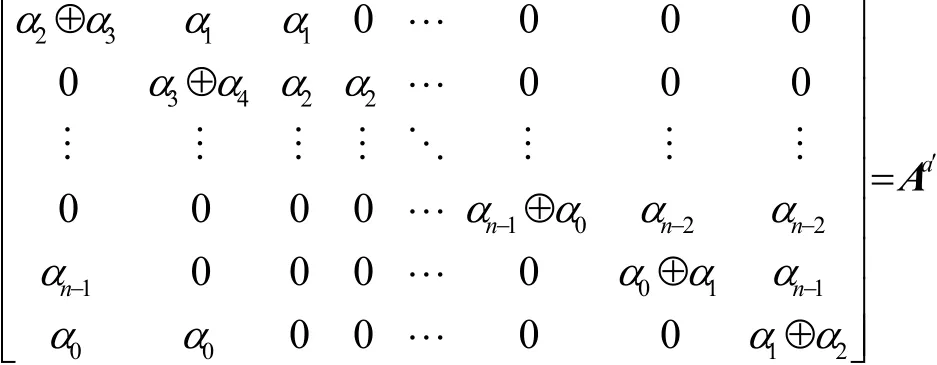
另外只需将上面的α替换成σ1(α)，α′替换成σ2(α)，就有k=2时成立。同样地，k为其他值时定理均成立，证毕。

定理 6设n≥5，对于，给定输入差分设α的汉明重量为w(α)，对于任意输出差分β，若，那么当或

证明当w(α)=1时，考虑α′=(0,0,…,0,1)时的情况，即而其余位置均为 0。此时将在Z2上进行初等变换，可以得到有3行非零的阶梯型矩阵所以此时A的秩r=3，由定理3可知，对于任意输出差分β，若。又由定理5，若w(α)=1，必然存在使得，所以时就有

当w(α)=n-1时，同样地，考虑时的情况，即α0′=0而其余位置均为1。此时，在2

Z上进行初等变换，可以得到有n-1行非零的阶梯型矩阵所以A的秩r=n-1。由定理3可知，存在2n-1个不同的β使。又由定理5，若必然存在使所以时就有

根据定理5可知，循环移位等价的2个输入差分对应的非平凡差分转移概率是相等的。从而本文可以根据循环移位等价将w(α)=2和w(α)=3时的α进行分类。

的输入差分α在w(α)=2时根据循环移位等价可以分为{σk(5)|k∈Z}={5,9,10,18,20}和2类。在w(α)=3时也可以分为和两类。由定理5可知，同一类中的输入差分对应相同的非平凡差分转移概率。经验证可知，{σk(5)|k∈Z}和{σk(11)|k∈Z}对应的非平凡差分转移概率记这2个集合的并集为；而{σk(3)|k∈Z}和{σk(7)|k∈Z}对应的非平凡差分转移概率，记这2个集合的并集为至此本文已经得到的输入差分α在w(α)=2和w(α)=3时对应的非平凡差分转移概率情况。

定理 7设的输入差分为α，其汉明重量为w(α)，对任意β∈Z5，如果当且仅当时，；当且仅当时

证明由于w(α)∈{0,1,2,3,4,5}。当w(α)=0时，或1；由定理6，当w(α)=4或w(α)=5时，若，则有，则有又根据上面的讨论，当w(α)=2或w(α)=3时，若α∈Ω1，，而当w(α)=1时，若则其对应的非平凡差分转移概率，而若α∈Ω，则其对应的非平2凡差分转移概率

表1 和的差分转移概率计数

表1 和的差分转移概率计数

差分转移概率 5 F 5 n e w F K 1 1 1 1 4 0 2 0 1 8 1 2 0 1 2 0 1 6 2 5 6 1 7 6 0 6 4 7 7 0 7 1

6 结束语

虽然目前有许多密码已经使用了基于元胞自动机的S盒，但都使用了Keccak的局部规则或者仿射变换。本文通过实验找到了一类新的基于元胞自动机的S盒并研究了其置换性质和差分性质，证明了该类S盒在规模为5时是一个置换，并且其非平凡差分转移概率的取值范围为而Keccack的S盒的非平凡差分转移概率的取值范围则为另外，本文进一步研究了该类S盒在规模为5时的差分分布情况，给出了该类S盒在取到最大和最小非平凡差分转移概率时的充要条件。最后通过比较和的差分转移概率的计数情况可以发现，相比差分分布更加均匀。所以该类S盒有着比Keccak类S盒更好的差分性质。接下来的工作重点是从理论上研究这类 S盒抵抗线性分析以及立方攻击[14]等各类攻击方法的效果。