带冲突检测的两阶段无连接接入协议最优资源分配

简鑫，王芳，宋健，付澍，谭晓衡，曾孝平

（重庆大学微电子与通信工程学院，重庆 400044）

1 引言

大规模机器类通信（mMTC, massive machine type communication）是5G定义的3个典型应用场景之一，是3GPP为智慧城市、智能能源、环境监测等以传感和数据采集为目标的应用场景提出的一种海量低功耗广域覆盖（LPWA, low power wide area）技术，面临海量连接、超低功耗、广域覆盖与深度覆盖、信令与数据相互触发等技术挑战[1-6]。当海量机器类终端（MTD, machine type device）短时间内同步入网时，其业务模式将表现出明显的瞬时突发特性，该特性将造成严重的承载网络流量过载或网络拥塞，尤其是资源稀少的无线接入网及其控制平面[5-9]。为缓解上述问题，研究者们提出了诸如分类受控接入（ACB, access class barring）、动态资源分配（dynamic resource allocation）、专属的退避机制（dedicated back-off）以及无连接或免调度接入（connectionless access or grant-free access）等候选解决方案。其中，前3类[5-6]为3GPP标准化进程中的过渡策略，期望通过充分利用和优化现有网络技术来承载 mMTC业务；无连接接入[10-11]作为5G mMTC的长期演进策略，允许MTD不需要建立无线承载（radio bearer）就进行小数据传输，可最大程度降低系统信令开销与 MTD能耗，是解决mMTC海量连接问题的重要研究方向。

无连接接入宏观上可分为一阶段无连接接入（OSCLA, one-stage connectionless access）和两阶段无连接接入（TSCLA, two-stage connectionless access）2类[10-11]。当采用OSCLA时，MTD直接以竞争随机接入的方式发送小数据分组，如时隙ALOHA及其改进型[12]；除极少的同步开销外，OSCLA几乎不引入额外的系统信令开销；但随着MTD数量的增加，随机接入冲突概率的增加将使OSCLA性能（如吞吐量、资源利用率等）急剧降低。上述问题可在一定程度上通过编码时隙ALOHA（coded slotted ALOHA）[12]或多前导单次随机接入（multiple preamble based single attempt random access）[13]等方式部分解决，是应用OSCLA之前必须重点突破的问题[14]。当采用TSCLA时，MTD需要发送调度请求（SR, scheduling request）后才能开始小数据分组发送；尽管发送SR会引入额外的时延，但TSCLA却可据此合理分配SR阶段和数据传输阶段的资源，达到提高系统吞吐量和最大化资源利用率的目的；更为重要的是，TSCLA的两阶段工作方式与现行蜂窝网的随机接入信道（RACH, random access channel）工作流程相仿，不需要过多协议修改即可应用[11,15]。简言之，OSCLA因采用竞争接入而更适合低负载场景的小分组传输，TSCLA因可合理地分配SR阶段和数据传输阶段资源配比而更适合中高负载场景。

TSCLA源于现行蜂窝网的两阶段资源预约型无线接入协议，根据其资源分配方式，可进一步分为3个子类。为描述方便，本文将这3个子类按序编号为TSCLA1、TSCLA2、TSCLA3，并将其工作原理概述如下[11,16-21]：1)TSCLA1为每一个SR申请（如前导码）指定一个固定的数据传输资源，而TSCLA2与TSCLA3不需要这样的一一对应关系；2)TSCLA2为每一个活跃的SR申请随机分配有限的数据传输资源，这需要基站反馈SR申请空闲或活跃（idle or active）的信息，即SR申请的两状态反馈（binary feedback）；3)TSCLA3为每一个成功的SR申请随机分配有限的数据传输资源，这需要基站反馈SR申请空闲、成功或冲突（idle, success or collision）的信息，即需在活跃SR申请的基础上进行冲突检测以反馈 SR申请的三状态信息（ternary feedback）。实现SR申请冲突检测的方法有将MTD身份信息与SR申请同时发送[16-17]、多用户检测或多分组接收技术[18]等。不同的资源分配方式使各TSCLA具有不同的最优资源分配策略，相关研究可概述为：1)TSCLA1工作原理简单，可视为一种静态资源分配策略，其性能分析将在本文第3.1节进行简要介绍；2)TSCLA2最优资源分配策略可参考现行蜂窝网RACH的相关研究[19-21]，例如，文献[18]推导了当用户数、SR资源和数据传输资源给定时，成功完成SR申请和数据传输2个阶段的用户数的概率密度函数，文献[19]完整地推导了当用户数和总资源数给定时，TSCLA2的性能极限与达到该极限时SR阶段与数据传输阶段的最优资源分配策略；3) 针对TSCLA3，仅文献[17]给出了SR阶段与数据传输阶段最优资源分配的穷举法数值解。基于此，为全面刻画TSCLA3的工作特点，本文进一步推导了TSCLA3的性能极限、SR阶段与数据传输阶段最优资源分配的解析解，此外，还提出了一种不需要用户数估计的自适应资源分配策略，在一定程度上消除了用户数估计误差对最优资源分配的影响。上述研究工作可为面向5G mMTC的无线接入协议的性能分析与优化设计提供重要参考[15,22]。

2 系统模型与建模假设

无连接接入允许MTD不需要建立无线承载就进行小数据传输。OSCLA工作流程可参照ALOHA类随机接入协议及其改进型。如图1所示，TSCLA工作流程可概述为：1) MTD发送随机选择的SR前导码申请小数据传输；2) 基站检测收到的SR前导码并据此分配数据传输资源，TSCLA1因前导码与数据传输资源之间存在一一对应关系而不需要该步骤，SR申请也退化为用户活跃检测[11]，TSCLA2为活跃的 SR前导码分配数据传输资源[11,20]，TSCLA3为成功的SR前导码分配数据传输资源[17]；3) MTD在相应的数据资源块上进行小数据传输；4) 基站反馈数据解调结果以指示 MTD下一步动作，如重传或休眠等。上述流程可通过改进现行蜂窝网RACH Msg3实现[10,15]。

图1 TSCLA工作流程

由图1可知，当且仅当MTD顺利完成SR申请和小数据传输这2个阶段后，基站才能正确解调MTD的上行数据。图2进一步描述了上行总资源给定时TSCLA的资源分配。不难理解，若SR阶段与数据传输资源分配失衡，系统无法达到最优性能。鉴于TSCLA1相对简单而TSCLA2的研究相对较多，本文重点研究TSCLA3的最大连接数或性能极限、SR申请与数据传输阶段的最优资源配比，以便为其优化设计提供理论指导。参照文献[17,20]，本文的建模假设和主要参数可概述为：1)基站具有理想的冲突检测功能；2)当前活跃的用户数为n；3)系统最小资源分配单元为时频资源块（RB, resource block），其总数为R；4)分配给 SR 申请的RB数目为RSR，每个RB可提供k个前导码，因此可用的前导码数目为m=kRSR，且每个前导码可供一个MTD进行一次SR申请；5)分配给数据传输的RB数目为Rdata=R-RSR，且每个RB可供一个MTD完成一次数据传输，每个RB支持不同数量前导码和不同数量MTD进行数据传输的情况，可通过线性变换等效为上述情况；6)实际场景中上述变量均为整数，但因为整数的实数近似与真实值的最大差值小于 1，所以为求解方便，本文将上述整数变量近似为实数变量。

图2 TSCLA的资源分配

3 理论推导

3.1 各TSCLA协议性能对比

本节首先完成各TSCLA协议的性能分析与对比，并据此给出TSCLA3的优势。TSCLA1为每一个SR申请指定一个固定的时频资源块，这意味着

那么，当采用TSCLA1时，成功完成数据传输的用户数ns等于SR前导码发送成功的用户数，即

当采用TSCLA2时，基站检测活跃的SR前导码并为其分配数据传输资源，其中活跃的SR前导码包含发送成功和冲突的SR前导码。目前，大多数蜂窝网的随机接入过程都采用这种方式。因基站会为冲突的SR前导码分配相同的时频资源块使其无法完成数据解调，此时只有发送成功的SR前导码才能完成数据传输。更进一步，当活跃的前导码数超过分配给数据传输的RB数目Rdata时，因基站为活跃的SR前导码随机分配数据传输资源块，此时只有一部分发送成功的SR前导码才能完成数据传输，其比例等于发送成功的SR前导码数与活跃的SR前导码数之比。据此，当采用TSCLA2时，成功完成数据传输的用户数可表示为[20]

当采用TSCLA3时，基站检测发送成功的SR前导码（即可检测冲突的SR前导码）并为其分配时频资源块。此时只要发送成功的SR前导码数据不超过分配给数据传输的RB数目Rdata，发送成功的SR前导码都可有效地完成数据传输，因此当采用TSCLA3时，成功完成数据传输的用户数可表示为[17]

对比式(2)～式(4)可知，当n、R、k固定时：1)TSCLA1可视为一种静态的资源分配策略并且具有固定的ns，其本质上与 OSCLA工作原理相同，当且仅当时，ns可取最大值ne-1；2) TSCLA2和TSCLA3的ns均与RSR相关且存在一个最优的RSR使ns最大；3) 当RSR在较大范围内变化时，TSCLA2和TSCLA3的ns均大于TSCLA1的n；4)因为s是归一化负载的单调递减函数且小于1，那么TSCLA2的ns一定小于TSCLA3的n，且s越大，两者差距越大，这意味着尽管TSCLA3具有更高的复杂度，但其特别适合应对mMTC的海量连接需求，又因为文献[20]详细分析了TSCLA2的性能极限和最优资源分配策略，本文将重点研究TSCLA3的相关内容。

3.2 性能极限：给定R和RSR时n的最大值

定理1当给定R和RSR时，TSCLA3支持的n的最大值nmax可表示为

与之对应的ns的最大值ns,max可表示为

证明由文献[17,20]的研究结论可知：当发送成功的SR前导码数等于分配给数据传输的RB数目Rdata时，TSCLA3的n与ns可取得最大值。将其应用于式(3)，上述条件等效为

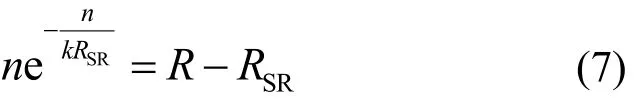
将式(7)两边同时除以-kRSR，可得

由朗伯W函数的定义可知，式(8)关于n的解可表示为

其中，Wx(⋅)表示第x类朗伯W函数[23]，x∈{0， 1}。因为nmax＞0，所以应属于区间。由R≤R可知，y必定小于或等于0，

SR即上述区间右边一定成立。由-e-1≤y可知

此时，可用的数据传输资源数将ns,max限定为。由朗伯W函数定义可知[21]：在区间内，-W(y)≥-W(y)。为了降低 SR-10前导码冲突概率，本文令x=0，即取朗伯W函数的上分支（upper branch）。式(5)与式(6)上半部分得证。

证毕。

定理2当仅给定R时，TSCLA3支持的n与ns的最大值可表示为

定理2的证明相对简单，可由式(5)与式(6)是关于RSR的凸函数直接得出，此处不再赘述。值得注意的是：1)与给出了TSCLA3的性能极限，其中可用于合理设置 ACB策略接入概率；2)给出了对应的最优资源分配策略。

3.3 最优资源分配：给定R和n时RSR的最优值

定理3当给定R和n，以最大化ns为目标时，TSCLA3分配给 SR申请的 RB数目的最优值由以下函数决定。

因为R总是固定的，所以为简单起见，式(12)和式(13)中关于的符号表示没有体现R。

证明是式(7)关于RSR的解，其解由式(8)给出。此时n作为自变量，其取值范围为[0,∞)，x=0或x=1的 2个解均为的可行解。当时，与{n,R}的关系由朗伯W函数的上分支决定；当时，与的关系则由朗伯W函数的下分支决定。式(12)得证。

由W0(⋅)与W-1(⋅)函数在范围内的性质可知：当时是关于n的单调递减函数；当时，是关于n的单调递增函数。因此在取得最小值，即。当时，n的最大值由s式(6)给出，即。式(13)得证。

3.4 不需要用户数估计的动态资源分配策略

当运用式(12)或图2对TSCLA3进行最优资源分配时，与大多数TSCLA2的最优资源分配算法类似[19-21]，必须辅之以精确的用户数n估计算法，否则难以避免的用户数估计误差将使偏离最优值，其中，为n估计值。用户数估计误差Δn给带来的偏差可由关于n的导数给出，可表示为

为避免上述问题，本文充分发掘TSCLA3协议检测发送成功或冲突SR前导码的能力，提出了一种不需要用户数估计的动态资源分配算法。所提算法将发送成功的SR前导码数与分配给数据传输的RB数目的差值作为反馈，以迭代方式逐步逼近，其工作原理为

其中，i表示第i个接入周期；与分别表示第i个接入周期发送成功的 SR前导码数、分配给SR申请和数据传输的RB数目。为初始化算法，RSR(0)和RSR(1)可取[]1,R-1内任意的不同值；为提高算法的收敛速度，令，其中，为第i个接入周期内的估计用户数，Δ0为一个微小的摄动量以避免无法初始化算法。式(15)的有效性可将其理解为在式(7)上运行Newton-Raphson算法[24]或将其视为由Δ(i)驱动的二阶闭环控制系统[25]。当运用式(15)作为 TSCLA3的最优资源分配时，图1的工作流程可以细化为：1)基站广播当前接入周期可用于 SR申请的资源块数目RSR、时频位置和前导码配置信息k等；2)MTD根据基站广播信息发送 SR申请；3)基站检测接入成功的SR申请并为其分配数据传输资源，并按照式(15)计算下一个周期的RSR；4)MTD 按照资源分配结果传输数据，基站接收MTD数据并反馈解调结果，然后返回步骤 1)完成新一轮的相关信息配置。上述过程因不需要用户数估计，可在一定程度上折中TSCLA3因检测发送成功或冲突的SR前导码而需要的复杂度，即充分发掘TSCLA3协议检测发送成功或冲突的SR前导码的能力。

4 数值分析

本节将通过数值分析验证第3节理论分析的正确性。为对比方便，本文令R和k的取值与文献[17]相同，即R=300，k=4。由定理 2可知，此时

图3的2条实线分别描述了nmax、ns,max与RSR∈的关系。由图 3可知：1)nmax与ns,max是关于RSR的凸函数；2)ns,max是关于RSR的线性分段函数；3) 当时，nmax与RSR呈线性关系；当时，nmax与RSR的关系由W0(⋅)函数决定；4)nmax与ns,max的最大值都在时取得，分别为与。图 3的 3条虚线分别描述了时ns与RSR的关系。由图3可知：1) 3种情况下的ns均小于或等于ns,max；2) 3种情况下的ns均为RSR的凸函数，分别在时取得最大值；3) 当RSR≥时，ns受限于Rdata；当时，ns受限于。上述结果验证了定理1～定理3的正确性。

图3 nmax、ns,max与RSR的关系（R=300）

为验证第3.4节所提算法的有效性，图5对比了所提算法与已知每个接入周期内用户数n的理想算法ns(i)的差别。这是因为尽管实际系统无法实现理想的用户数估计，但其代表了这类算法的性能上限；当给定某类用户数估计算法时，其估计误差对TSCLA3性能的影响也可由式(15)和图4给出。图5所采用的业务到达过程为接入强度同λ时所提算法与理想算法ns(i)的平均比值（i∈[1,1000]内的平均）。由表 1可知：1) 当λ在较的分段泊松过程；为表示方便，每个段内仅取40个接入周期。由图 5可知：1) 除在每个段的开始几个接入周期存在较大的波动外，所提算法将快速收敛到与理想算法一致的结果；2) 理论上所提算法的性能肯定会比理想算法差，但图5的仿真结果表明该差别在可接受的范围内。为衡量该差别，表1列出了不大范围内变化时，所提算法比理想算法的性能损失在4%以内；2)越小，所提算法的性能损失越小，这与式(15)的结论类似。上述结果验证了所提算法的有效性，即可利用较少的性能损失实现不需要用户数估计的最优资源分配。

图4 (n)、( n)与n的关系（R=300）

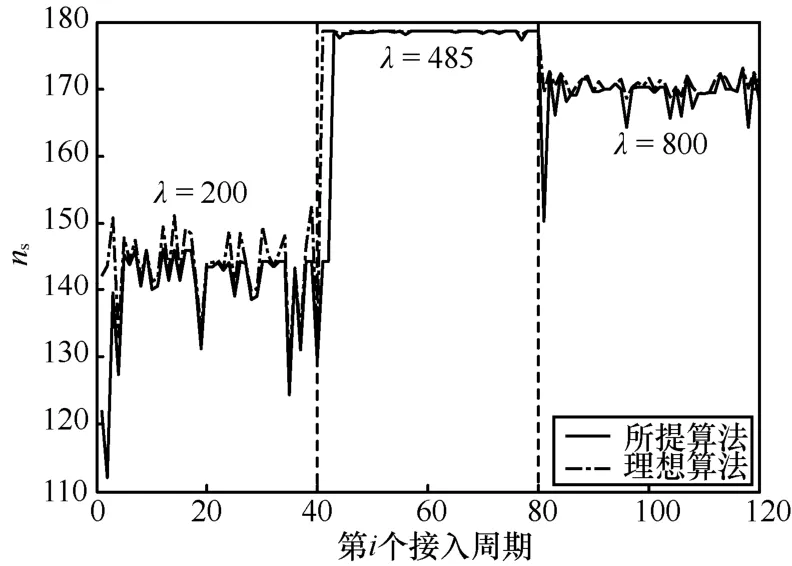
图5 所提算法与理想算法ns( i)的对比

5 结束语

以最大化成功完成数据传输的用户数为目标，本文完成了一类称作带冲突检测的两阶段无连接协议的性能极限与最优资源分配策略的理论分析，分别给出了其可支撑的最大用户数与分配给发送调度请求申请的资源块数目的最优值。为避免因用户数估计误差造成最优资源分配策略的性能损失，本文还设计了一种不需要用户数估计的动态资源分配算法。数值仿真表明，所提算法与已知每个接入周期内用户数的理想算法的性能差异在 4%范围内。上述研究工作可为 mMTC相关的无线接入协议的最优资源分配提供参考。下一步工作为将上述工作扩展到非理想信道状态反馈或多重反馈的场景以完善5G无连接协议的相关研究工作。

表1 不同λ时所提算法与理想算法ns( i )的平均比值