无速度传感器控制的全功率变流器风电系统研究

李玉东 李传伟 王鹏

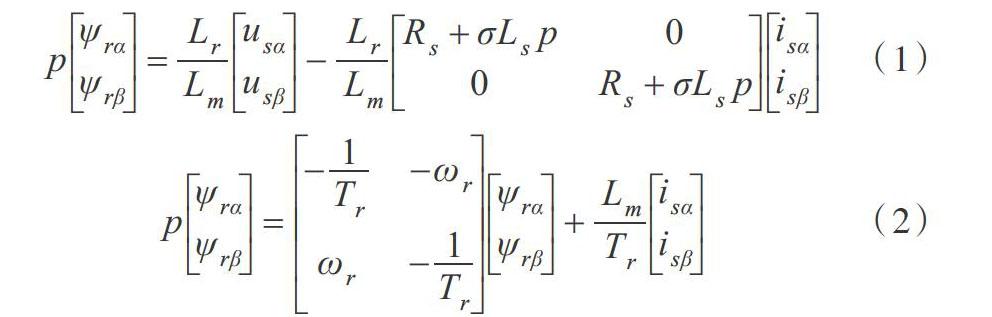
摘 要：鉴于传统控制策略在鼠笼式电机风力发电全功率变流器稳定性、控制性能、效率与可靠性方面存在明显缺陷，跟据感应发电机的特点，提出一种基于模型参考自适应算法的不带速度传感器控制策略。根据Popov超稳定性定理，设计该控制算法速度估计方案，最后通过仿真验证控制效果。仿真图形显示，在仿真过程中速度估计值随实际值变化，并且误差较小，控制系统稳定、效率高，验证了该方案可行性。

关键词：风力发电;笼型感应发电机;无速度传感器;全功率变流器

Abstract： For squirrel-cage wind power full-power converters， traditional control strategies have obvious shortcomings in stability， control performance， efficiency and reliability. In view of the above deficiencies， according to the characteristics of the induction generator， this paper proposes a control strategy based on model reference adaptive algorithm without speed sensor; according to Popovs super stability theorem， this control algorithms speed estimation scheme is designed， and the control effect is verified through simulation. The simulation graph shows that in the simulation process， the speed estimation value changes with the actual value， and the error is small， the control system is stable and the efficiency is high. The feasibility of the proposed solution is thus verified.

Key Words： wind power generation; squirrel cage induction generator; speed-sensorless control; full-scale converter

1 引言

當今世界普遍关注的两大问题分别是环境污染和能源短缺，世界各国对新能源探索开发的投资不断加大，其中风能开发利用方便、投资少、效率高，所以风力发电得到了迅速发展。风力发电机组种类较多，优缺点各异，其中全功率变流器的鼠笼感应发电机组具有电力系统简单、保养成本低、控制性能可靠等优势，被广泛应用于风电机组。因此，进一步提高全功率变流器性能，提高机组控制性能、效率与可靠性意义重大。

海上风电力发电的不断发展，要求风电机组不仅要有优良的控制能力，还要具有很高的可靠性。由于机械位置传感器常常安装在电机中，造成了费用增加、体积变大引起维护不便等弊端[1-2]，大量研究人员对不带速度传感器控制的风电机组进行了研究。文献[3]提出基于不带速度传感器的全功率变换器风力发电机侧的控制策略，发电机侧变换器采用基于模型参考自适应算法的不带速度传感器直接转矩控制，电网侧变换器采用电压以及电流闭环控制。实现感应电机不带速度传感器控制需要知道转子或定子磁链值，但磁通量不能直接测得，通常需要观测器估计电机磁链值。传统的磁通估算方法使用电流、电压模型，通过测得电机工作时的电压、电流以及转速信号观测转子磁链，然而该方法鲁棒性低且观测精度不高[4]。文献[5-6]根据李雅普诺夫稳定性原理设计了基于龙贝格观测器的全阶磁通观测器，并成功估测了电机转速信号。文献[7]给出了一种基于转矩电流动态的降阶磁链观测器，该方法的不足之处在于需假设负载转矩不变。文献[8]设计了一种基于根轨迹的自适应磁链观测器，并研究了该观测器构建的稳定性。近年来许多高性能的观测器被应用到电机系统中，例如非线性观测器[9]、滑模观测器[10-12]以及扩展卡尔曼滤波器[13-14]等，有效处理了非线性问题。

开环位置估计方案可利用电压积分法或采用迭代方法进行磁链估计[18-19]、基于反三角函数的实时计算[20]，但因缺乏自我修正能力，使估计结果受电机参数等因素影响，如模型参考自适应系统（MRAS）及其参考模型闭环方案需积分器处于理想状态，定、转子电流或磁链通常作为驱动自适应机制调节信号，利用比例积分算法获取位置或速度信号[21-22]，然而实际的积分器存在积分漂移，致使位置估计精度不高。其它闭环方法有全阶观测器[23-24]和锁相环（Phase-locked Loop，PLL）[25]，前者的难点是需确定各类负载条件才可选取最佳增益，状态的初始值也影响观测器收敛性能;而后者观测精度较依赖于电机参数。

基于以上观测器存在的缺点，本文设计一种基于双PWM变频器的笼型感应电机风力发电系统，发电机侧变换器使用基于MRAS的无速度传感器控制。本文采用MRAS方法对发电机转速进行估计，并提出一个能有效抑制磁链与转速观测器设计中积分器初值影响的方案，通过仿真论证了MRAS转速估计实现算法正确性。

2 基于MRAS的转速辨识理论分析

2.1 基于MRAS的转速估计方法

MRAS是一种自适应控制手段，鉴于其良好的稳定性、鲁棒性且收敛速度很快，常被应用于自动控制及参数辨识领域[26-27]。MRAS包括参考模型和可调模型两个部分，可调模型中未知参数的识别可以通过可调模型与参考模型状态误差的自适应控制实现。Schauder首次使用MRAS 的方法估计交流电机转速，Lyapunov方程和Popov超稳定性理论确保了转速误差系统的渐进稳定。通过分析转子磁链、发电机反电动势的特性，可将其作为可调模型以实现速度估测。通过坐标变换，可得[αβ]坐标系下发电机转子磁链方程。

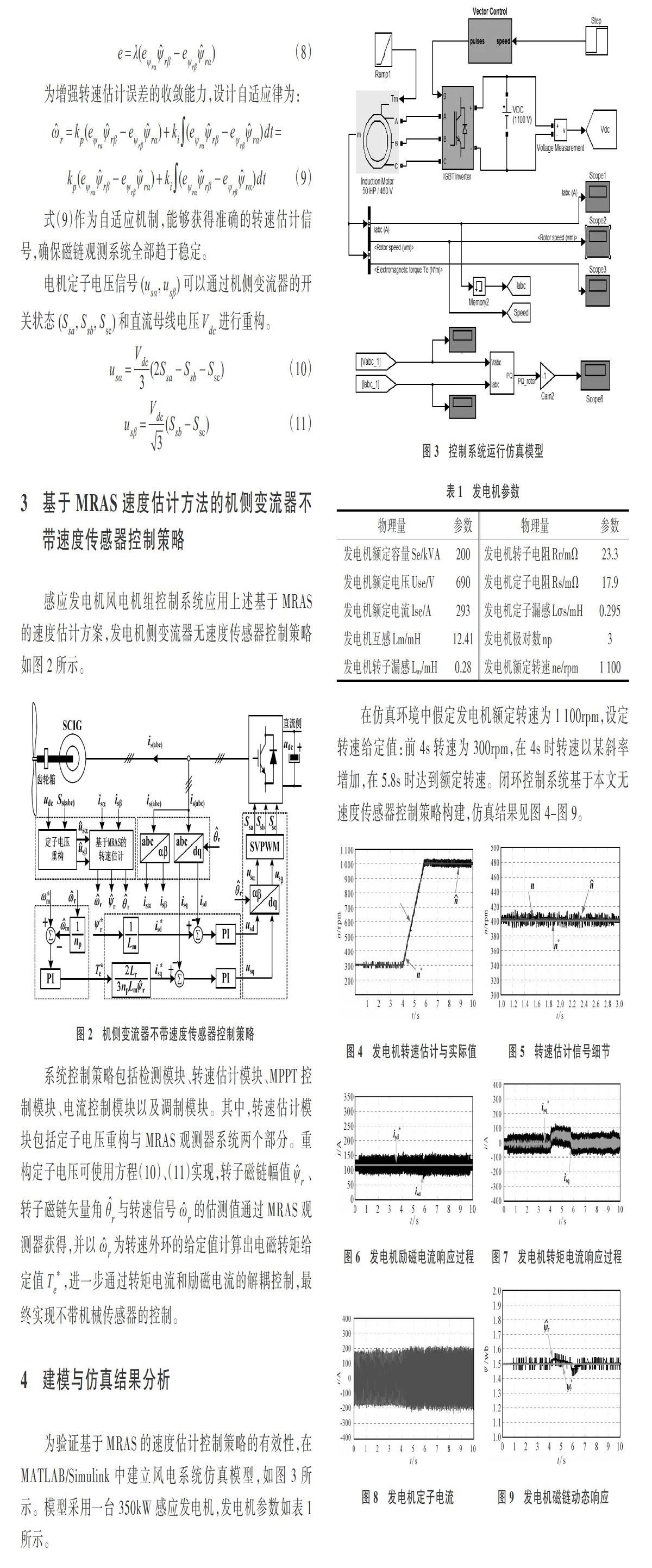
其中，[Tr]为转子时间常数，[p]为微分算子。

观察上述转子的电磁暂态关系式可以看出，式（1）是转子磁链的电压模型，式（2）是转子磁链电流模型。由于方程（2）包含旋转速度的物理量，所以把转子磁链电流模型作为MRAS的可调模型。同时，因为转子磁通不能直接测量，可采用方程（1）作为转子磁链的参考模型。基于MRAS方法的转速估计原理如图1所示。

2.2 MRAS速度估计方法自适应机理

在MRAS方法中，应用Popov超稳定性理论确保估计值逐渐收敛于实际值，通过自适应机制实现，见图1的自适应方法，其设计过程如下所示。

由转子磁链的电流模型实现磁链估计，其表达式为：

由公式（2）、（3）取系统误差状态为：

则磁链误差方程为：

要使转子磁链观测系统全局趋于稳定，根據Popov超稳定性判据，存在常数[γ]，在任意[t1]≥0时，满足Popov积分不等式：

其中，e为跟踪状态的误差矩阵。

将[e=eψrαeψrβ]，[W=0-eωeω0ψrαψrβ]代入式（5），可知要使系统全部趋于稳定，需满足：

根据不等式

可知，为使式（6）成立，可将转速误差[eω]设置为：

为增强转速估计误差的收敛能力，设计自适应律为：

式（9）作为自适应机制，能够获得准确的转速估计信号，确保磁链观测系统全部趋于稳定。

电机定子电压信号[（usα，usβ）]可以通过机侧变流器的开关状态[（Ssa，Ssb，Ssc）]和直流母线电压[Vdc]进行重构。

3 基于MRAS速度估计方法的机侧变流器不带速度传感器控制策略

感应发电机风电机组控制系统应用上述基于MRAS的速度估计方案，发电机侧变流器无速度传感器控制策略如图2所示。

系统控制策略包括检测模块、转速估计模块、MPPT控制模块、电流控制模块以及调制模块。其中，转速估计模块包括定子电压重构与MRAS观测器系统两个部分。重构定子电压可使用方程（10）、（11）实现，转子磁链幅值[ψr]、转子磁链矢量角[θr]与转速信号[ωr]的估测值通过MRAS观测器获得，并以[ωr]为转速外环的给定值计算出电磁转矩给定值[Te？]，进一步通过转矩电流和励磁电流的解耦控制，最终实现不带机械传感器的控制。

4 建模与仿真结果分析

为验证基于MRAS的速度估计控制策略的有效性，在MATLAB/Simulink中建立风电系统仿真模型，如图3所示。模型采用一台350kW感应发电机，发电机参数如表1所示。

在仿真环境中假定发电机额定转速为1 100rpm，设定转速给定值：前4s转速为300rpm，在4s时转速以某斜率增加，在5.8s时达到额定转速。闭环控制系统基于本文无速度传感器控制策略构建，仿真结果见图4-图9。

由图4可以看出转速信号[n]可以很好地跟踪转速给定值[n？]，从图5可以看出实际转速与估计转速的误差可以限制在1.5%以内以跟踪转速定值，且具有良好的稳态性能。图6-图9分别为机侧变流器系统中各电气量的动态响应，由此可知，控制系统状态良好。

由仿真结果可知，采用该观测器构成的机侧不带速度传感器控制策略，其风电机组控制性能良好，转速估计值可稳定跟随实际值，且误差较小，能满足工程应用要求。

5 结论

本文采用基于MRAS的控制算法进行电机转速辨识，实现了风电系统中机侧变流器无速度传感器的有效控制。仿真结果验证了转速估计及其闭环控制方案的可行性，为进一步提高电机风电机组控制可靠性提供了理论依据和具体方法。

参考文献：

[1] 杨淑英，张兴，张崇巍，等. 基于转子电流偏差角的双馈感应电机速度观测[J]. 电力系统自动化，2009，33（4）：92-95.

[2] HOLTZ J. Sensorless control of induction machines——with or without signal injection[J].  IEEE Transactions. on Industrial Electronics， 2006， 53（1）： 7-30.

[3] JANSEN P L， LORENZ R D. A physically insightful approach to the design and accuracy assessment of flux observers for field oriented induction machine drives[J]. IEEE Transactions on Industry Applications， 1994， 30（1）： 101-110.

[4] KUBOTA K，SATO I，TAMURA Y，et al. Regenerating-mode low-speed operation of sensorless induction motor drive with adaptive observer[J]. IEEE Transactions on Industry Applications，2002，38（4）： 1081-1086.

[5] MONTANARI M，PERESADA S M，ROSSI C，et al. Speed sensorless control of induction motors based on a reduced-order adaptive observer[J]. IEEE Transactions on Control Systems Technology， 2007， 15（6）：1049-1064.

[6] ZAKY M S. Stability analysis of speed and stator resistance estimators for sensorless induction motor drives[J].  IEEE Transactions on Industrial Electronics， 2012， 59（2）： 858-870.

[7] ALEMI-ROSTAMI M，ABRISHAMIFAR A. Nonlinear observer for induction motor to improve efficiency and dynamic stability analysis in FOC method[J]. Journal of Circuits，Systems， and Computers， 2012， 21（1）：1250011-1250011_33.

[8] YAN Z， JIN C， UTKIN VI. Sensorless sliding-mode control of induction motors[J]. Industrial Electronics， IEEE Transactions on， 2000， 47（6）： 1286-1297.

[9] PROCA A B， KEYHANI A. Sliding-mode flux observer with online rotor parameter estimation for induction motors[J]. IEEE Transactions on Industrial Electronics， 2007， 54（2）： 716-723.

[10] TURSINI M，PETRELLA R，PARASILITI F. Adaptive sliding-mode observer for speed-sensorless control of induction motors[J]. IEEE Transactions on Industry Applications， 2000， 36（5）： 1380-1387.

[11] MONTANARI M， PERESADA S， TILLI A. A speed-sensorless indirect field-oriented control for induction motors based on high gain speed estimation[J]. Automatica， 2006， 42（10）： 1637-1650.

[12] KIM Y R，SUL S K，PARK M H. Speed sensorless vector control of induction motor using extended Kalman filter [J]. IEEE Transactions on Industry Applications， IEEE Transactions on，1994，30（5）： 1225-1233.

[13] BARUT M， BOGOSYAN S， GOKASAN M. Experimental evaluation of braided EKF for sensorless control of induction motors[J]. IEEE Transactions on Industrial Electronics， 2008， 55（2）： 620-632.

[14] 梅柏杉，吳迪，冯江波，等. 无速度传感器笼型感应电机风力发电控制[J]. 电机与控制应用，2014，41（3）：47-50.

[15] 杨勇，阮毅. 风力发电中PWM逆变器交流侧电感的设计[J]. 太阳能学，2009，30（3）：355-360.

[16] HOPFCNSPCRGCR B， ATKINSON D J，LAKIN R A. Stator flux oriented control of a doubly-fed induction machine with and without position encoder[J]. IEE Proceedings of the Electric Power Applications， 2000，147（1）：241-250.

[17] 黄晟，廖武，黄科元. 双馈风力发电系统无速度传感器控制[J]. 电气传动，2010，40（3）： 3-5.

[18] CARDCNAS R，PCNNA R，Clare J C， ct al. MRAS observers for sensorless control of doubly-fed induction generators[J]. IEEE Transactions on Power Electronics， 2008，23（3）： 1075-1084.

[19] ABOLHASSANI M， ENJCTI P，TOLIYAT H. Integrated doubly fed electric alternator/active filter （DEA），a viable power quality solution， for wind energy conversion systems[J]. IEEE Transactions on Energy Conversion， 2008，23（2）：642-650.

[20] JAIN A K，RANGANATHAN V T. Wound generator with sensorless control and filter for feeding nonlinear loads in a   rotor induction integrated active stand-alone grid[J]. IEEE Transactions on industrial Electronics，2008，55（1）：218-228.

[21] 高乐. 双馈感应风力发电机控制系统关键技术研究[D]. 长沙：湖南大学，2010：13-87.

[22] YANG S， AJJARAPU V. A speed-adaptive reduced-order observer for sensorless vector control of doubly fed induction generator-based variable speed wind turbines[J]. IEEE Transactions on Energy Conversion， 2010，25（3）：891-900.

[23] SCHAUDER C. Adaptive speed identification for vector control of induction motors without rotational transducers[J]. Industry Applications， IEEE Transactions on， 1992， 28（5）： 1054-1061.

[24] YANG G，CHIN T H. Adaptive-speed identification scheme for a vector-controlled speed sensorless  inverter-induction motor drive[J]. IEEE Transactions on Industry Applications，1993，29（4）： 820-825.

[25] 王慶龙， 张崇巍， 张兴. 交流电机无速度传感器矢量控制系统变结构模型参考自适应转速辨识[J]. 中国电机工程学报， 2007， 27（15）： 70-74.

[26] 齐放，邓智泉，仇志坚，等.  一种永磁同步电机无速度传感器的矢量控制[J]. 电工技术学报，2008，22（10）：30-34.

[27] LANDAU Y D. Adaptive control： the model reference approach[J].  IEEE Transactions on Systems， Man and Cybernetics，1984（1）： 169-170.

（责任编辑：江 艳）