基于NPE改进算法的人脸识别

王族 闫德勤 何阳 娄雪

摘 要：邻域保持嵌入（NPE）算法与极端学习机结合后应用到人脸识别中没有达到令人满意的识别效果，为找到更优的解决方案，提出一种改进的邻域保持嵌入算法（SNPE）。在SNPE算法中将NPE目标式子与带有类间判别信息的式子做减法，通过极小化目标函数，达到最小化同一类别领域距离且最大化不同类别领域距离的目的。通过Yale人脸数据库、Yale B人脸数据库、ORL人脸数据库等实验结果表明，改进后的算法大幅提高了人脸识别率。

关键词：邻域保持嵌入算法;流行学习;人脸识别

DOI：10. 11907/rjdk. 182389

中图分类号：TP301文献标识码：A文章编号：1672-7800（2019）002-0009-04

Abstract： The combination of the neighborhood persistence embedding （NPE） algorithm and the extreme learning machine does not achieve a satisfactory recognition effect when applied to face recognition. In order to find a better solution， this paper proposes an improved neighborhood persistence embedding （SNPE） algorithm. In the SNPE， we subdivide NPE object subtypes with equations with inter-class discriminant information， minimize the distance between the same category and maximize the distance between different categories by minimizing the objective function. Through experiments such as the general Yale face database， Yale B face database， and ORL face database， the improved algorithm is proved to greatly improve the recognition rate in face recognition.

Key Words： neighborhood persistence embedding algorithm;manifold learning;face recognition

0 引言

人脸识别作为信息鉴别的一种常用手段，在公安、遥感、银行等部门及领域均有相当广泛应用，但在实践中大多数数据均为高维数据，且存在分布不均匀的现象，因此对研究数据进行有效维数约减十分重要。

基于现有维数约减方法发展出很多数据降维改进算法。Kirby & Turk等[1-2]将主元分析法（Principal Component Analysis，PCA）引入到人脸识别降维算法中，后续还包括线性判别分析（Linear Discriminant Analysis，LDA）[3-5]。这两种算法共同缺点是没有考虑数据几何结构，即人脸图像易受表情、脸部姿态、人脸形状和皮肤及光照等内外在因素影响，为了避免该问题，研究者相继提出了几种非线性流行结构降维方法[6]：等距映射法（Isometric Feature Mapping，Isomap）[7]、局部線性嵌入算法（Locally Linear Embedding，LLE）[8]及LE（Laplacian Eigenmaps）[9]算法，但由于以上算法会出现样本外问题，无法直接用于人脸识别。之后有学者提出域保持嵌入算法（Neighborhood Preserving Embedding，NPE）[10-12]，该算法在选取近邻点时采用欧式距离计算方法，造成重构误差[13-14]，且在进行线性重构时NPE算法没有考虑到样本点间的判别信息。

针对上述问题，本文在NPE基础上进行改进， 改进后算法不仅继承了传统NPE方法的优点， 而且因目标函数中加入类间判别信息，并用极端学习机（ELM）分类器[15]进行分类，该方法能增强样本点间的判别能力，更加准确地实现数据降维。为了证明本文SNPE算法有效性，将其与LMMDE、RAF-GM、NPE算法在人脸数据集上进行比较，实验结果证明本文算法优于其它对比算法，并在降维问题上取得了良好效果。

2 邻域保持嵌入算法

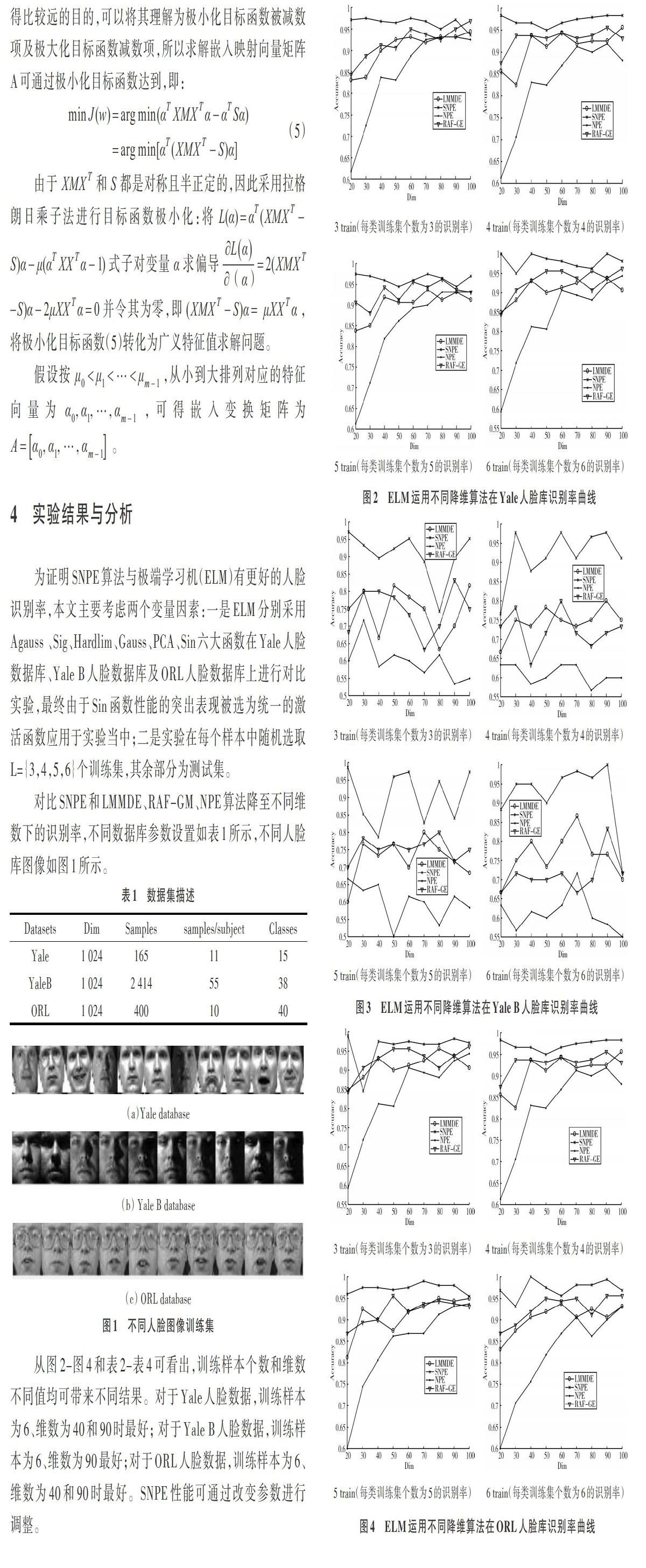
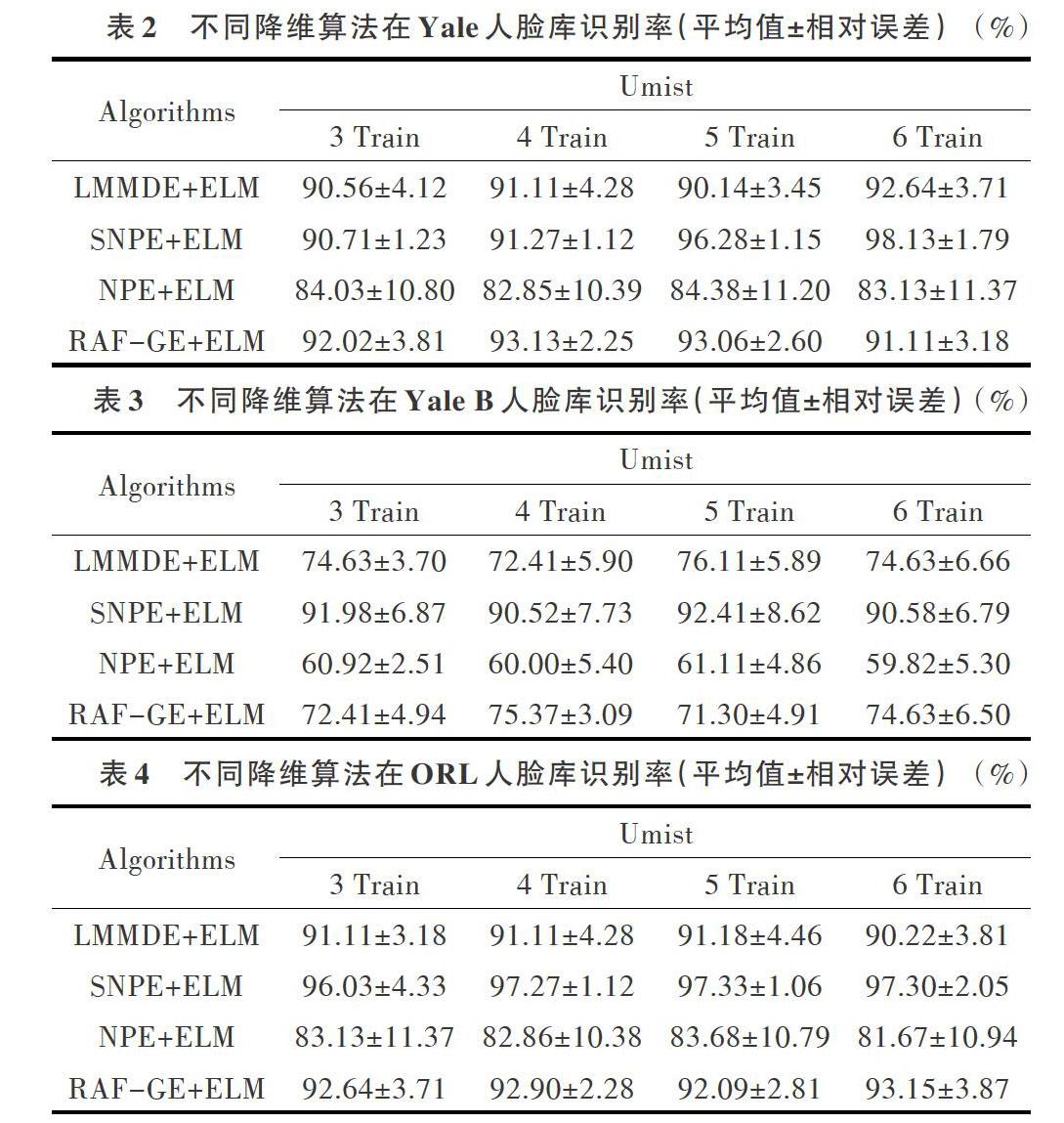
邻域保持嵌入（NPE）算法是一种局部特征提取算法，与其它算法相比主要有两个优点：一是能够充分挖掘高维数据的局部信息，二是可解决数据非线性特性。假设高维数据由[X=x1，x2，？，xd，xi/xi？Rn]空间降到相对低维空间[X=y1，y2，？，yd，yi/yi？Rm（m

（1）选取数据样本点[xi]的k个欧式距离最近的近邻点[xj]，连接[xi]和[xj]。

（2）计算权重W。高维[Rn]空间中权重系数矩阵可以通过[φ（W）=ixi-jWijxj2]（约束条件为[jWij=1，][j=1，][2？N]）求得，[Wij]既能在[Rn]空间中重构[xi]，也能在[Rm]空间中重构[yi]，因此有[φ（y）=iyi-jWijyj2]，又由于NPE假设每个局部近邻是线性的，则有[yi=ATxi]，经过代数运算可化简为[φ（y）=ATXMXTA]，其中[M=（I-W）T（I-W），][I=][diag（1，1？1）]，约束条件变为[ATXMXTA=1]。

（3）求解特征映射。利用拉格朗日乘子法可将求解[φ（y）]的最优化问题转化为求解特征值的问题，即[XMXTA=μXXTA] ，设按[μ0<μ1<？<μm-1]从小到大排列所对应的特征向量为[α0，α1，？，αm-1]，最终求得由[Rn]空间映射到[Rm]空间的坐标为[yi=ATxi]，式中[A=（α0，α1，？αm-1）]。

3 基于NPE改进的邻域保持嵌入算法

由于人脸图像数据存在信息冗余及噪音，会对ELM泛化能力造成影响，因此本文提出一种改进的稀疏邻域保持嵌入算法（SNPE）。SNPE算法主要特点包括：①该方法不仅能在固定权重的情况下使类内局部邻域线性重构误差最小，而且能增强样本点之间的判别能力，使得在[Rm]空间内的数据集具有最大的类间距离;②应用到人脸识别时，会遇到小样本问题，即未经处理的人脸数据维数较高且训练样本数又很少，可能造成类间离散度矩阵[S]是奇异矩阵，为避免该类问题本文算法采用减式而非除式。

将给定的N个训练样本集[X=（x1，x2，？，xN）∈Rn]分为c类，记为[X=（x1，x2，？，xc）]。则[Y=（y1，y2，？，yc）]代表嵌入映射数据集[Y=（y1，y2，？，yN）∈Rm]的c类低维数据集。[xci]表示第[c]类第[i]个数据样本，第[c]类数据样本个数为[nc]。

基于上述假设，SNPE理论框架可由优化公式（1）得到。

其中，[yci]和[ycj]分别为第[c]类样本的第[i]个和第[j]个低维嵌入向量，[Wcij]为[yci]和[ycj]的重构权重系数，[ωc]和[ω]分别为第[c]类样本低维均值向量和总体样本低维均值向量，再通过代数运算对目标函数进行简化。SNPE继承了NPE在降维时能保持数据集固有的局部邻域结构不变的优点，因此假设线性变化向量为[α]，则[YT=αTX]。

（1）被减数化简。

（2）减数化简。

（3）求解嵌入映射向量矩阵A。为达到降维时同类样本点内部几何结构不变，不同类样本点间信息尽可能映射得比较远的目的，可以将其理解为极小化目标函数被减数项及极大化目标函数减数项，所以求解嵌入映射向量矩阵A可通过极小化目标函数达到，即：

4 实验结果与分析

为证明SNPE算法与极端学习机（ELM）有更好的人脸识别率，本文主要考虑两个变量因素：一是ELM分别采用Agauss 、Sig、Hardlim、Gauss、PCA、Sin六大函数在Yale人脸数据库、Yale B人脸数据库及ORL人脸数据库上进行对比实验，最终由于Sin函数性能的突出表现被选为统一的激活函数应用于实验当中;二是实验在每个样本中随机选取L={3，4，5，6}个训练集，其余部分为测试集。

对比SNPE和LMMDE、RAF-GM、NPE算法降至不同维数下的识别率，不同数据库参数设置如表1所示，不同人脸库图像如图1所示。

从图2-图4和表2-表4可看出，训练样本个数和维数不同值均可带来不同结果。对于Yale人脸数据，训练样本为6、维数为40和90时最好; 对于Yale B人脸数据，训练样本为6、维数为90最好;对于ORL人脸数据，训练样本为6、维数为40和90时最好。SNPE性能可通过改变参数进行调整。

图2-图4分别给出ELM运用不同降维算法在Yale、Yale B及ORL人脸数据集上的识别率曲线，从中可以看出SNPE算法的识别率与LMMDE、NPE、RAF-GE算法相比有大幅度提升，在Yale B 人脸数据集上表现极为明显，但在不同维数上的识别率不是很稳定。ELM运用于Yale及ORL人脸数据集上的识别率相对稳定，且准确率接近100%。表2-表4进一步证明了以上结论，并充分说明：①SNPE算法較原始的NPE算法有更好的识别率;②在Yale和ORL人脸数据集上的识别率基本达到90%以上且较稳定，在Yale B人脸数据集上识别率较低但也明显高于其它算法。因SNPE结合ELM算法充分考虑样本点之间的结构信息，NPE算法更能准确地在复杂环境下实现人脸识别，

5 结语

人脸识别自提出以来受到广泛关注，并且在实际生活中得到了很好的普及。本文算法将类间离散度矩阵作为判别信息加入到目标函数中，进行了一次有意义降维算法尝试。SNPE算法能够有效地对人脸识别数据维数进行约减，减少了计算量，提高了ELM泛化性能。通过SNPE与LMMDE、RAF-GM、NPE的对比实验表明，本文方法在人脸图像实验中取得了良好的分类效果。下一步研究重点是将SNPE应用于其它图像分类任务中，进一步验证本文算法泛化性能。

参考文献：

[1] LLC Member Representatives Committee. Digital Cinema Initiatives， LLC Digital Cinema System Specifications V1.0[EB/OL]. http：//www.dcimovies.com.

[2] ADAMS M，WARD R. JasPer：a portable flexible open-source software tool kit for image coding/processing[C]. Montreal： International Conference on Acoustics， Speech， and Signal Processing，2004.

[3] 李瑞敏，陆化普. 基于WebGIS的智能交通管理指挥调度系统[J].  计算机工程，2007，33（21）：232-234.

[4] SCHMITT E J，JULA H. Vehicle route guidance systems： classification and comparison[C]. Proceedings of IEEE Intelligent Transportation Systems Conference， 2006： 242-247.