一种区域经济发展差异分析智能混合算法及应用*
韦艳玲
(柳州职业技术学院,广西 柳州 545006)
0 引言
20世纪90年代以来,涉及各层级的中国区域经济发展差异问题一直是研究热点,其中常见的传统数量研究方法包括变差系数(加权变差系数)、锡尔系数、基尼系数、量图分析、标准差、熵指数等.[1-6]国内运用数据挖掘技术测度区域经济发展差异方面的研究刚刚起步,用数据挖掘技术来分析经济发展差异一般采用聚类方法.聚类方法很多,常用的研究分析方法包括K-均值聚类法、模糊聚类、层次聚类、神经网络等.[7-11]准确度较高的有FCM、K-means,层次聚类准确度最差,神经网络算法则耗时最长;[12]而一般聚类是硬划分,不合适解决多因素、界限模糊的分类问题.有学者用神经网络进行经济发展状况分类,但没有考虑到样本各变量的相互影响,而且没有进一步优化参数,这会使预测精度下降、效率降低.有关模糊分类方法也需要进一步研究,如消除原有数据的相关性和降维,以及分类的合理性等.
模糊聚类是解决多因素、不清晰界限的一个有效办法,而模糊C-均值聚类算法(FCM)[13]是其他的模糊聚类方法的理论和应用的基础.但是,FCM算法属于局部搜索优化算法,初始值选择不当会引发结果达不到全局最优,而用遗传算法可以有效解决初始值选择不当问题,遗传算法的早熟问题可由模拟退火算法有效解决.[14]在笔者前期研究中,采用遗传模拟退火算法应用于西部省区经济发展分类和服务业分类取得了较好的效果.[15-16]
经济指标之间一般存在相关性,主成分分析法可以消除相关性,得到新的主成分作为聚类的初始数据,而采用主成分距离加权聚类分析法能使聚类效果更好.[17]
从聚类准确度方面和地区经济发展差异研究的特点考查多种方法,本文提出一种区域经济发展差异分析智能混合算法:拟先采用FCM算法对西部各省份经济发展水平进行分类,再采用主成分分析法给西部各省份经济发展水平进行综合评分.为了得到更好的分类效果,使用本文提出的基于主成分距离加权的遗传模拟退火优化FCM算法进行聚类.
本文以西部省份经济发展差异为例,依据所提出的区域经济发展差异分析智能混合算法,对西部省份经济发展差异进行综合分析.
1 区域经济发展差异分析智能混合算法
1.1 FCM算法
FCM算法是一种基于目标函数的模糊聚类算法,其思想是该分类使目标函数J值最小,[13]同一簇对象之间的相似度最大.
FCM算法表示:

其中U为其相似分类矩阵,V是各类别的聚类中心点,c为要划分的类别数,d ij为第i个数据样本与第j类中心点之间的欧氏距离,μij∈ [0,1]是样本x i对于j类的隶属度,β∈[1,∞)是一个加权参数,当β∈[1.5,2.5]效果最好.[18]
1.2 主成分距离加权算法
由于主成分因子的贡献率不一样,第一主成分贡献率最大,其次为第二主成分,再次为第三主成分,以此类推.它们在分类时的重要性是有主次之分的,主成分因子直接代替原始数据的后果是使分类失真,所以在计算样本之间距离时要给出不同的权重,以达到自适应样本数据的目的.
设G1,G2,…,G d是所提取的各主成分因子列向量,I1,I2,…,I n为提取主成分后新的行向量,所对应的贡献率为α1,α2,…,αd,d为新属性个数.则样本I i与样本I j距离表示为:
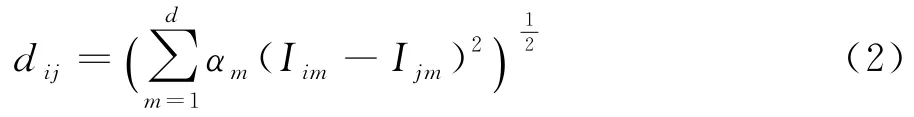
1.3 基于主成分距离加权的FCM算法
根据公式(2),对FCM算法进行改进,得到新的基于主成分距离加权的FCM聚类算法表示如下.

其中d为新属性个数.
根据拉格朗日乘数法,上面的算法可转化为下列式子:

τi是拉格朗日乘子.
对式(4)中的目标函数J(U,V)求极值,则可对参数τi、μij求偏导数,取值为0,得到下列式子:

求得隶属度μij的值为:

式(7)是目标函数最小化的充分条件,是使目标函数最小化的隶属度μij值的迭代式.
聚类中心值的迭代式为:

公式(7)和公式(8)用于迭代修改数据隶属度、聚类中心,当算法收敛时,确定了各聚类中心,也确定了各样本对于各类的隶属度,完成了分类工作.
1.4 主成分距离加权和遗传模拟退火优化的FCM算法(以下称本文优化的FCM算法)
本文优化的FCM算法流程如图1所示.图1中i为遗传进化次数循环计数变量,T为当前温度,K为温度衰减系数.
1.5 区域经济发展差异智能混合算法
(1)采用本文优化的FCM算法对区域经济各经济体进行聚类,分析不同类别经济体的特征.
(2)采用主成分分析法给各经济体经济发展水平进行综合评分,得到各经济体的经济发展排名.
(3)依据分类和评分情况,对区域经济发展差异进行研究分析.

图1 本文优化的FCM算法Fig.1 The optimized FCM algorithm in this paper
2 西部省份经济发展综合评价指标体系构建及数据说明
2.1 指标体系构建
参考相关文献,选取3类10项指标以反映西部12省份经济发展状况,即规模指标(2个)为GDP(X1)、固定资产投资总额(X2),结构指标(3个)为第二产业增加值比重(X3)、服务业增加值比重(X4)、常住人口城镇化率(X5),质量指标(5个)为人均GDP(X6)、地均GDP(X7)、人均社会消费品零售额(X8)、居民人均可支配收入(X9)、每万人口国内专利申请授权量(X10),这10项指标在很大程度上反映了基础设施建设、产业结构调整、创新能力提升、社会事业进步等西部大开发战略中的重要方面.
2.2 数据说明
采用的原始数据均来源于2016年《中国统计年鉴》及西部各省份统计年鉴.
3 西部省份经济发展差异实证分析
3.1 聚类分析
下面以2015年的西部省份经济发展状况分类为例详细说明聚类的具体过程和步骤.
3.1.1 数据预处理
采用Z-score标准化方法对原始数据进行标准化处理.
3.1.2 确定主成分和方差贡献率
由主成分分析得到前3个主成分的方差贡献率88.1%>85%,如表1所示,每个主成分由各原始指标线性组合,设新的综合指标为F1、F2、F3,主轴(对应主成分)信息表如表1所示.

表1 主轴(对应主成分)信息表Tab.1 The spindle(corresponding principal component)information table
3.1.3 实验参数选择
算法参数设定如表2所示.

表2 参数设定表Tab.2 The parameter setting table
实验说明:
加权参数β试取1.5、2、2.5等数值分别做试验,结果显示,对于2015年的相关数据,选择加权参数β=2能使样本的划分更分明.
3.1.4 聚类分析
当划分模糊度越小时,样本集的划分越分明,则分类越好,因此,对于给定的加权参数β,如果划分模糊度最小时,便得到最好分类.
划分模糊度的定义为:
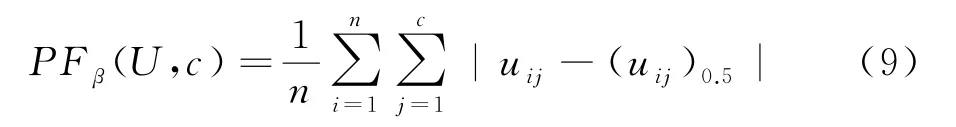
其中:n为样本个数,c是聚类个数,U是模糊划分矩阵,
采用本文优化的FCM算法进行聚类后,当分为6类时,划分模糊度PFβ(U,c)为最小值,目标值在多次重复运行中一直稳定,划分模糊度PFβ(U,c)均为最小,故最好分类定为6类.分为6类时模糊划分矩阵U对应的西部各省份隶属度值如表3所示.

表3 西部各省份隶属度值Tab.3 The membership value of western provinces
表2中元素U ij表示j省属于i类的隶属度.为了进一步分辨隶属强度,以利于分析,用稍弱、较弱等在其后标注.例如:如果最大隶属度的值小于0.9且大于等于0.8,说明属于这类的程度是稍微弱的,在其后标明“稍弱”;如果最大隶属度的值小于0.8且大于等于0.6,说明属于这类的程度是比较弱的,在其后标明“较弱”.由以上分析得到2015年西部省份的初步分类如表4所示,表中的类别排序大体按照经济发展状况综合评分的高低排序.下同.

表4 经济发展状况分类Tab.4 The classification of economic development
3.2 西部各省份经济发展水平评分及排名
由3.1.2节中得到三个主成分和对应的方差贡献率,把三个主成分与对应的方差贡献率相乘并累加,得到2015年西部省份经济发展状况综合得分,并且对其进行排名.综合得分及排名如表5所示.

表5 经济发展状况综合得分及排名Tab.5 The comprehensive score and order of economic development
3.3 结果分析
2015年,受全球经济不景气的影响,全国绝大部分省份经济增速减缓,但重庆仍以GDP增速11%与西藏并列第一.重庆是中西部唯一的直辖市,也是西部大开发重要的战略支点,是 “一带一路”和长江经济带的重要联结点,在中国宏观经济下行压力的背景下,重庆却以GDP增速连续3年逾10%领跑全国,成为中国经济快速转型发展的样板之一,综合实力名列西部第一,在西部各省份中独立为一类.内蒙古2015年经济总量为西部第三,人均GDP为第一,而内蒙古所走的资源型经济发展道路与其他省份区别明显,所以分类时单独为一类.陕西是西北地区经济发展较好的省份,经济总量为西部第二,其经济结构与四川、广西较为相似,故与四川、广西分为一类.广西虽然经济总量2015年名列全国第17位,2016年名列全国第18位,但与作为西部重要增长极的四川、陕西分为同一类,说明广西具有与四川、陕西类似的经济结构特征,发展潜力很大,有望发展为西部的重要增长极.西藏从始至终都分为单独的一类.由于历史及地理原因,西藏交通不便,本土人才少,经济基础薄弱,大大限制了发展,是全国经济总量最小的省份.西藏在2015年GDP增速引领全国,2016年GDP增速10%名列全国第三,但并不代表其具有经济快速增长的内生动力,而更多是由于落后,国家加大投资项目倾斜.青海、宁夏缺乏国家级新区、城市群、支边援边等区域政策扶持,经济发展缓慢,有边缘化危险.
4 结论
从对西部各省份经济发展差异的应用分析来看,本文所提出来的区域经济发展差异分析智能混合算法应用较好,同时探索、检验了数据挖掘等新型技术在经济研究中的应用有效性,在区域经济发展差异分析上有广阔的应用前景.

