基于Savitzky-Golay滤波算法的FY-2F地表温度产品时间序列重建

吴迪， 陈健， 石满， 覃帮勇， 李盛阳

(1.南京信息工程大学遥感与测绘工程学院，南京 210044； 2.中国科学院空间应用工程与技术中心太空应用重点实验室，北京 100094)

0 引言

地表温度(land surface temperature, LST)在地—气间物质与能量交换过程中起着重要作用，是全球及区域尺度地表物理过程研究的关键参数，对生态、环境、水文、气象气候、生物地球化学以及农业生产等研究具有重要意义[1-2]。传统气象站点可实时观测获取LST，但受站点分布、地形等因素影响，具有一定局限性且空间不连续[3-4]。随着遥感技术的发展，目前已有许多传感器可提供空间连续的LST产品，如EOS/MODIS，NOAA/AVHRR和FY/VISSR等，其中MODIS LST产品在天气晴朗条件下精度可达1 K[5]。然而，受到云、气溶胶、观测角度和太阳光照角度等影响，各种LST产品在时间和空间上均存在不同程度的缺失[6]，这限制了LST遥感产品的应用。时间序列数据重建技术可以充分利用多种统计或数值分析方法，模拟LST的时间变化规律，从而插补缺失的观测值[7-8]，因此利用时间序列重建技术重建LST数据，进而得到较高时空分辨率的LST产品具有重要意义。

针对遥感反演的LST存在大量缺失值的情况，已有许多学者基于MODIS等数据开展了LST的重建研究。Nguyen等[9]利用归一化植被指数(normalized difference vegetation index,NDVI)时间序列谐波分析法(harmonic analysis of NDVI time-series，HANTS)重建越南红河三角洲MODIS LST数据，并分析了该地区LST及土地利用时空变化规律； Neteler[10]提出了一种基于LST直方图识别云污染像元的方法，并根据温度梯度重建了MODIS LST数据； 臧琳等[11]基于统计模型和滤波算法联合的LST重建方法建立LST与地表亮温的统计模型，然后利用滤波算法对基于统计模型的结果进行插值，基于LST时间序列的周期性进一步控制反演误差。以上研究均有效重建了MODIS的LST数据，并进行了更加深入的应用。但是，这些研究大多是针对MODIS等极轨卫星数据开展的研究，目前，针对静止卫星LST产品的重建研究仍比较缺乏。相较于极轨卫星，静止卫星能够提供1 d内多个时相的观测数据，可更准确地获取LST的时间变化规律，为准确进行LST重建提供了更多的信息。

风云2号卫星是我国自主研发的第一代地球同步轨道静止气象卫星，由2颗试验星(FY-2A，B)和5颗业务星(FY-2C，D，E，F，G)组成，并根据观测数据制作了多种定量产品数据。风云卫星可以提供包括LST在内的多种遥感反演产品，其中LST分为逐时、日平均、候平均、旬平均及月平均产品。本文基于FY-2F LST日数据，利用LST随时间变化规律，基于Savitzky-Golay(S-G)滤波算法，对2013年长江三角洲(下文简称长三角)地区LST进行数据重建，以填补LST的缺失值，提高LST产品的可用性。基于该方法重建的FY-2F LST时间序列数据，可为长三角地区热环境研究提供较好的数据基础。

1 材料与方法

1.1 研究区概况

长三角位于中国大陆东部沿海，是中国第一大经济区。根据国务院2010年批准的《长江三角洲地区区域规划》，长三角包括江苏省、浙江省和上海市2省1市，区域面积为21.07万km2。其中上海市为平原； 江苏省以平原为主，间或有一些山地丘陵； 浙江省多山地。整个长三角地区水网密布，自然资源丰富。属亚热带湿润季风气候区，夏季高温多雨，年均气温为15～17 ℃，年降水量约为1 000～1 800 mm。

长三角地区地理位置优越，并且具有良好的经济基础，在中心城市带动下经济快速蓬勃发展，城市化进程也随之加速[12]。伴随着经济活动、城市化进程，长三角地区城市空间热环境日益恶化，对环境、生态及人体健康造成极大的危害[13-14]。而LST是研究区域热环境的重要因子，因此对长三角地区LST进行重建，从而获得较高质量的产品数据，对研究区域热环境变化情况具有重要的意义。

1.2 数据源

FY-2F是静止气象卫星风云二号03批的首发星，于2012年1月成功发射，搭载了2个主要载荷(扫描辐射计和空间环境监测器)。FY-2F提供包括LST在内的多种遥感反演产品，LST产品数据可从国家卫星气象中心的风云卫星遥感数据服务网(http: //satellite.nsmc.org.cn/portalsite/default.aspx)免费订购下载。

FY-2F卫星能够提供时间分辨率高达1 h的LST产品，为探究不同时间分辨率的数据质量，分别统计了2013年长三角地区逐时产品及日产品的空间缺值率(即一景图像空间上的缺值率)，结果如表1所示。

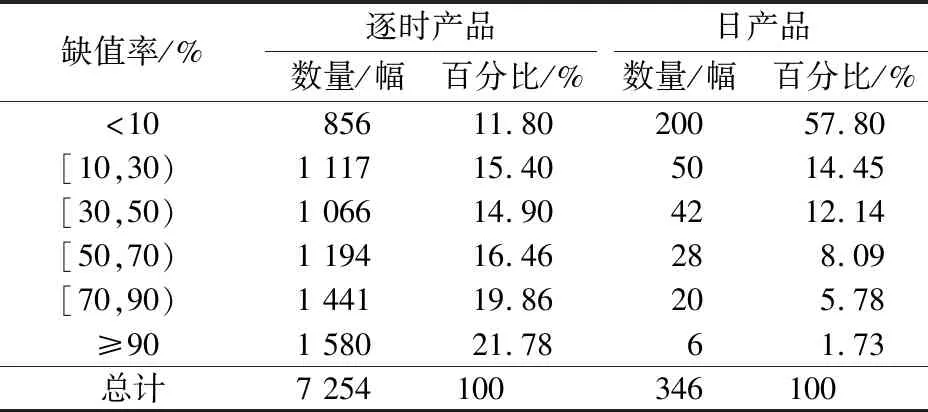
表1 FY-2F LST产品空间缺值率统计

从表1中可以清楚地看到，FY-2F LST逐时产品空间缺值率较大，全年空间缺值率超过90%的影像高达21.78%； 相较于逐时产品，日LST数据质量显著提高，全年有57.80%的数据空间缺值率低于10%，仅有1.73%的影像空间缺值率大于90%。考虑到逐时产品的缺值率过高，重建难度较高，且在研究长时间尺度地表热环境变化时，应用日产品效果更佳，因此将对FY-2F LST日产品进行重建以便更好地进行后续研究。本研究数据采用2013年FY-2F LST日均值产品，该数据存储为HDF5格式，星下点空间分辨率为5 km，每幅影像可获取覆盖地球表面约1/3的圆盘标称影像。由于数据不具备投影和经纬度信息，因此根据风云卫星遥感数据服务网提供的经纬度数据进行了几何纠正。

气象数据为2013年长三角地区气象站点日平均LST观测数据。长三角地区共有46个气象站点(江苏省23个，浙江省22个，上海市1个)，空间分布如图1所示，该数据可从中国气象数据网免费下载(http: //data.cma.cn/site/index.html)。

图1 研究区气象站点分布示意图

1.3 基于S-G滤波的LST重建方法

受研究区内云量、传感器等因素影响，LST遥感数据存在数值异常或缺值现象，FY-2F LST逐时数据即存在大量缺值，即使是每日合成产品仍存在很多无效像元，严重影响了数据的可用性，因此能否精确地重建LST数据就尤为重要。本文基于LST长时序变化特征，并结合滤波算法重建LST缺值。S-G滤波由Savitzky和Golay[15]在1964年首次提出，是一种在时域内基于局部多项式最小二乘拟合的滤波方法。通过取点xi相邻时相(前后)固定个数点拟合多项式，多项式在xi的值即为S-G滤波的模拟值。该滤波器最大的特点为在滤除噪声的同时可以保持曲线的变化趋势。在对FY-2F LST数据重建的过程中，S-G滤波方法能够最大程度地保留原始数据，并且根据相邻数据模拟出缺值。S-G滤波过程可表示为

，

(1)

当像元长时间连续缺失较多数据时，若单纯使用S-G滤波进行数据重建则可能与真实值相差较大。针对这一问题本文筛选出某像元一段不存在缺值的数据作为研究对象，从该段数据中分别提取1～5个相邻时相数据不参加S-G滤波，模拟出像元不同连续缺值情况，并将重建前、后LST值进行对比。图2中绘制出原始LST和5条不同连续缺值重建后曲线，方框代表模拟缺值，从图中可以清楚地看到连续缺失数据越多，模拟结果与原始LST差值越大，当连续缺失达到5个数据时误差大于3 K。

图2 不同连续缺值重建效果

因此，本文首先遍历每一像元所有时相LST数据，并根据像元连续缺值情况将全年数据拆分为若干组，当连续缺失5个及以上时相数据时该段LST不进行重建。随后，根据实测数据统计出LST最大、最小值作为阈值，判断LST异常点，利用接口描述语言(interface description language，IDL)函数库提供的S-G滤波函数重建异常点及缺失数据，并且保留原始有效数据不变，通过反复迭代达到最佳拟合效果。S-G滤波函数需设定窗口宽度m及多项式拟合阶数Degree，通常情况下m值越大滤波结果越平滑；Degree一般设定在2～4范围内，阶数越低滤波结果平滑，但会带来误差，较高阶数可降低此项误差但“过拟合”会带来噪声影响滤波结果[16-17]。为了确定S-G滤波LST重建最优参数，本文在连续30 d数据中随机选择5 d数据并赋为缺值，再按照窗口宽度m=3,5,7及阶数Degree=2,3,4组成9组参数组合进行S-G滤波，经实验平滑窗口宽度m取5，阶数Degree为4时模拟LST与原始值最为接近。

2 结果与分析

2.1 LST重建结果

本研究对2013年FY-2F LST时间序列数据进行了重建，通过IDL函数库提供的S-G滤波函数迭代拟合，最终达到最优拟合效果。S-G滤波能够很好地将FY-2F LST数据缺失值补充完整，图3展示了长三角地区每一像元点重建前、后时间序列缺值率(即表示每个像元点长时间序列上的缺值率，下文简称时相缺失率)。经统计，长三角地区重建前FY-2F LST平均时相缺失率为19.43%，其中单一像元最少缺失9.54%数据，最高时相缺失率则达到39.31%，整个长三角地区南部数据时相缺失率高于北部。经过重建后，FY-2F LST时相缺失率明显降低，长三角大部分区域LST补充完整，平均时相缺失率下降至1.69%，可见S-G滤波方法具有良好的重建效果。

(a) 重建前时相缺失率 (b) 重建后时相缺失率

为了更直观地展现LST重建效果，图4选取不同空间缺值率的FY-2F LST原始数据与重建后数据进行对比。从图中可以看到，S-G滤波利用LST时序变化特征进行数据重建，重建效率较高，即便研究区内空间缺值率超过80%也能很好地完成重建工作，且能够较好地保证LST空间一致性。

(a) 20130204重建前(b) 20130316重建前(c) 20131221重建前(d) 20130716重建前

(e) 20130204重建后(f) 20130316重建后(g) 20131221重建后(h) 20130716重建后

为了从LST时间序列角度评价重建效果，本文进一步选取了南京站点作为验证点，对比站点实测值与重建前、后LST随时间变化曲线，如图5所示。

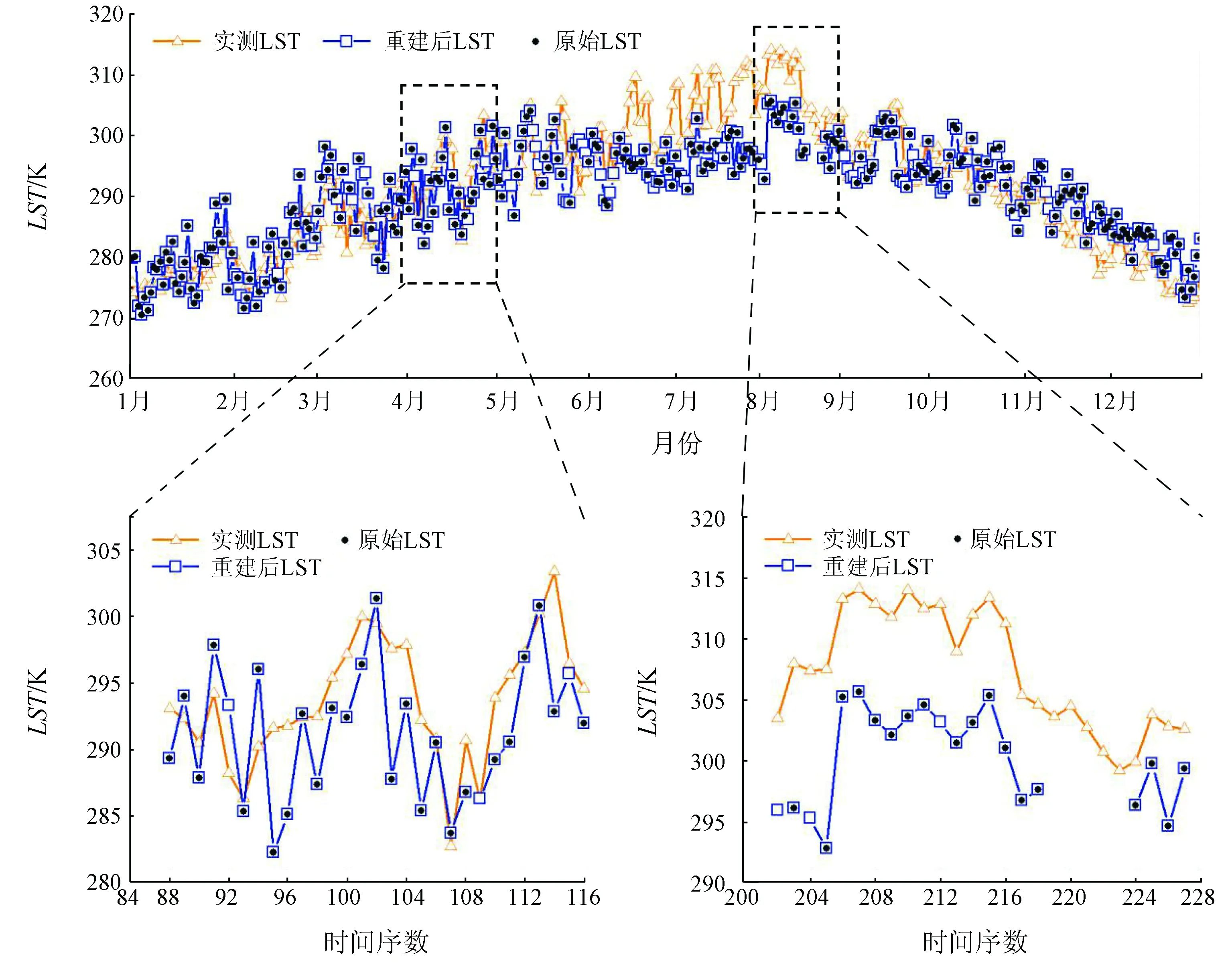
(a) 2013年

由南京站点2013年LST随时间变化总体曲线(图5(a))可以看出，本文重建方法可以有效地保留原始LST，并达到对缺值进行补充的目的。实测数据与重建前、后LST相比变化趋势一致，全年整体随时间变化先升高后降低。从图中也能看到，重建后的LST时间序列与实测数据仍然存在一定的误差，其中8月份的差值达到了10 K左右。为了更清楚地观察重建效果，分别提取4月及8月份数据如图5(b)和(c)。S-G滤波方法对LST时间序列进行滤波获取其长时间变化趋势，结合相邻时相点对缺值进行补充，使其符合LST变化规律。图5(b)中，实测数据与重建后FY-2F LST变化趋势较为一致，相邻2个时相FY-2F数据波动更大； 8月份(图5(c))存在连续缺失数据较多的情况，为了保证重建数据准确性该段缺值未进行补充，其余部分缺值经S-G滤波拟合效果较好，但与实测LST差值偏大，这种情况受数据本身精度的影响较大。

2.2 精度验证

为了进一步定量检验重建后LST结果的精度，根据经纬度提取了长三角地区46个气象站点重建前、后LST每日数据，并与相应日期实测LST数据进行对照。图6(a)和(b)分别展示了气象站点实测数据与LST重建前、后对比情况。从图中可以看到FY-2F LST原始产品与实测数据具有较好的拟合精度，判定系数R2为0.75，而平均绝对误差(mean absolute error,MAE)为4.88 K，原始LST产品精度较低。重建后样本数由11 201个增加至13 621个，R2及MAE与重建前基本保持一致，因此利用S-G滤波对FY-2F LST进行重建能够保证数据精度，重建结果较为可信。

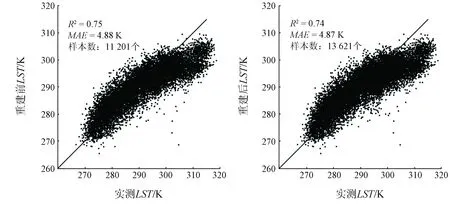
(a) 实测值与重建前LST (b) 实测值与重建后LST

经过对比发现，气象站点实测值与重建后LST值误差较大，主要有以下3点原因： ①FY-2F原始LST产品在某些地区误差较大，甚至超过10 K,由图5可以看出，高误差像元主要出现在夏季7—8月份，这可能受FY-2F LST产品本身反演算法的影响，也可能是该地区夏季云量较多，导致逐时数据缺失，进而影响了日平均LST数据的计算； ②气象站点实测值为“点数据”，而FY-2F LST数据为“面数据”，且空间分辨率为5 km，导致像元多为混合像元，由于两者尺度不同，在匹配时必然带来一定误差[18-19]； ③本文是在FY-2F LST产品的基础上进行重建的，受原始产品质量影响，无法解决一些时相的高误差问题。因此，重建后产品与重建前产品相比更加合理。

综合以上分析，为了更加明确S-G滤波方法重建效果，本文随后采取人工模拟缺值的方法排除由于数据问题导致的影响，对比重建前、后数据验证S-G滤波重建数据的准确性(图7)。

图7 重建前、后LST散点图

通过随机选取一些非缺值区域不参与S-G滤波，然后跟滤波之后的LST结果进行对比。选取验证点的时候，要求在长三角地区内均匀分布，且影像按照不同季节随机抽取，最大程度保证了验证结果的准确性。从图7中可见，重建前、后LST的MAE为1.35 K，R2为0.95，大部分样本都位于1∶ 1线附近，重建后LST与原始值吻合度较好。因此，除去数据质量等其他因素影响，利用S-G滤波方法进行数据重建效果良好。

为了进一步评价本文重建方法的鲁棒性，本文使用相同方法对2014年和2015年FY-2F LST日均值数据进行了重建，评价其R2和MAE，结果如表2所示。2014—2015年间站点实测值与重建前、后LST的R2和MAE基本持平，能够保证重建后LST数据精度不变； 人工模拟缺值点验证结果良好，与2013年结果大体相同，模型鲁棒性较好。

表2 2014—2015年LST重建精度评价

3 结论

本文利用S-G滤波方法，结合LST时间序列变化特征，对长三角地区FY-2F LST产品进行了数据重建，并对重建结果进行了评价。结果表明：

1)长三角地区FY-2F LST原始产品平均时相缺失率为19.43%，S-G滤波方法能够有效地重建LST，重建后平均时相缺失率降低为1.69%。并且对于不同空间缺值率影像，该方法均能在保持LST空间一致性的基础上对其进行有效重建。

2)提取长三角地区46个气象站重建前、后LST值，结合站点LST进行精度验证与误差分析。重建后结果精度与重建前FY-2F LST产品基本持平，但与实测值间误差较大，其原因为： 产品本身质量影响了重建结果精度； 进行验证时，实测值为“点数据”，与遥感“面数据”因尺度问题会进一步扩大误差。

3)通过人为模拟验证区缺值，将重建后结果与重建前对比，发现重建精度较高，两者R2为0.95，MAE为1.35 K。通过重建2014—2015年间FY-2F LST日均值产品验证S-G滤波模型适用性，其结果与2013年大体相同，表明S-G滤波法可以用来进行LST重建。

本文在保持FY-2F LST原始产品精度的基础上进行数据重建，能够有效提高产品质量，为地表热环境研究提供数据基础。然而文中重建采用的S-G滤波方法仅考虑了LST时序变化规律，并未利用到其空间信息。在今后的研究中可结合多源遥感数据和下垫面特性等因子进行空间上的重建，进一步提高产品数据质量。