异构蜂窝通信网络的发展及优化*

王金燕

（山东科技大学，山东 青岛 266590）

0 引 言

大数据时代背景下，爆炸性增长的网络通信流量使得频率成为需求为无线通信网络设计中的新要求：如何使用有限的频率为用户提供更好的服务质量，同时尽量降低系统耗能，建立绿色高速的通信网络。传统的蜂窝网络采用同构方式，仅使用大功率的宏基站提供通信服务。但是受维护成本的限制，宏蜂窝基站不能被密集布设，这就导致无线网络信号的发射出现了盲区。在任意两无线电基站最大覆盖范围的交界处，用户可能得不到很好的服务效率。针对同构网络的这一局限性，人们设计出了异构蜂窝网络。简单而言，异构蜂窝网络就是在大功率基站的信号薄弱区或者业务热点地带密集布设一些低功率基站进行信号覆盖，以数量上的优势弥补覆盖范围的不足，降低系统总耗能，提高用户的通信速率。

目前，异构蜂窝网络形式多样。一类仍保留传统蜂窝通信的异构形式，在小基站层次上继续划分，引入微站点、飞蜂窝站点、家庭基站等更小型基站；另一类采用其他通信方式的加强覆盖，如将Adhoc网络嵌入到蜂窝网络[1]。但是，在多用户接入情境下，绝大多数用户都会接入功率较高的宏蜂窝基站。一方面，宏蜂窝基站将会因为大量用户的涌入造成通信拥塞。另一方面，密集布设的小蜂窝基站则发挥不到理想中的辅助作用，只能白白浪费能源。

为了解决此问题，本文从异构蜂窝网络的组成结构出发，将其面临的负载不均衡问题抽象为约束函数优化模型。按照贪婪的启发式算法将优化问题形象化描述为类背包问题进行迭代，获得可行次优解。最后进行仿真实验，比较传统分配方式和本文提出的基于对数效用约束最优模型，验证了方案对于提高网线通信网服务质量的合理性。

1 异构蜂窝网络中的约束优化模型

1.1 约束条件下的最优化模型及分类

最优化模型有两种表现形式：函数优化模型和组合优化模型。二者的主要区别在于：函数优化问题中是在一定区域范围的连续值中确定使目标函数达到最优的一个点。而组合优化问题是从一个离散点集中求得一个组合变量使目标最优。

1.2 KKT条件求解函数优化

KKT（Karush-Kuhn-Tucker）条件是在多约束非线性规划问题中确定最优点的必要条件。即只要某个点满足在一定附加条件下达到最优，则该点一定满足KKT条件。特别的，对于凸优化问题，KKT条件既是最优点存在的必要条件也是充分条件。设：x*∈I,I(x)={i|gi(x*)=0,1≤i≤l}，f(x)与gi(x)（i∈I(x*))在点x*处可微，gi(x)在点x*处连续，hj(x)( j=1,2,…,m) 在点x*处连续可微，并且向量集{Δgi(x*),Δhj(x*)| i∈I(x*), j=1,2,…,l}线性无关。若x*是问题（1）的局部最优解，则存在：

使得下述条件成立：

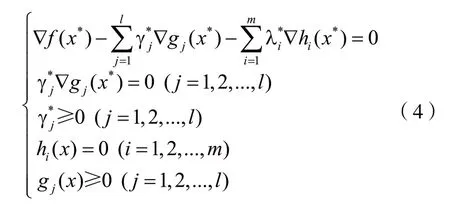
式（4）就是既含有等式约束又含不等式约束的非线性规划问题的KKT条件[2]。

1.3 启发式算法求解组合优化

所谓启发式算法，是相对于复杂问题的最优化提出的一种算法。当目标函数是规模较大的问题时，常规算法很难求解，只能基于直观和经验构造一种算法近似求解原问题，在允许的偏差范围内，花费一定的时空复杂度，给出一个符合条件的次优解。

1.4 约束优化模型在异构蜂窝网络中的应用

异构蜂窝网络是以传统的宏基站为工作核心，辅助以密集的小基站，如图1所示。

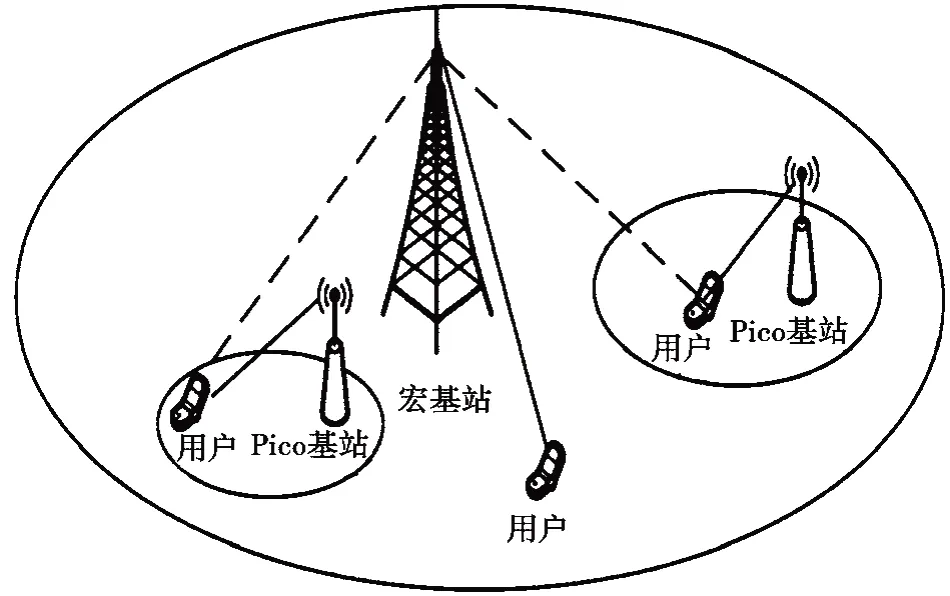
图1 异构蜂窝网络结构

由于宏基站的服务能力远强于小基站，当多用户接入时，如果不进行合理分配，会导致负载不均衡现象，导致通信网络的拥塞现象。由于每个基站的功率和资源是确定的，我们只需要确定如何分配用户与基站的接入关系和资源分配比例，使得整个网络系统中用户速率的对数效用函数最大。

建立模型之前，变量定义如下：

B：基站的数目；

U：用户的数目；

ri,b：b基站单独服务用户i时的传输速率；

ai,b：用户i是否接入基站b（其中ai,b=0或1，为0表示不接入，为1表示接入）；

xi,b：基站b为用户i分配的资源比例。

则每个用户在单个基站上所获得的服务质量：

整个优化模型可以描述为：

根据式（6）可知，该优化模型的解是一定区域内离散取值的量，属于组合函数优化。若按照实际生活中无线通信网络的覆盖范围，则该问题的求解时间呈指数级别，利用KKT条件求解最优点显然不再适用。因此，本文采用组合优化模型中的启发式算法，在一定时空消耗内求问题的一个可行次优解。下面我们首先对问题进行转化。

设{a(i)i,b}为一组满足所有约束条件的用户资源分配优化向量，则上述优化问题可以转化为：

则：

将式（8）带入到式（7），可以改写为：

至此，原问题已经转化成符合整数规划的类01背包问题。其中，B个用户相当于B个背包，一个用户只允许接入一个基站即一个背包只允许装如一件物品。已知单位物品价值为进行装包决策，优化总物品价值达到最大。

下面套用背包问题的贪婪思想迭代求解a(i)i,b。

i,b=1；否则a(i)i,b=0，迭代次数k:=k+1；

步骤3：当k=U时，迭代停止；否则重复步骤2：

最终所得{a(i)i,b}即为满足约束条件的一组次优解，算法的时间复杂度为UO（U+B）。

2 仿真实验

在本文模拟的异构蜂窝型通信网络中，设定了区域范围为500 m×500 m的正方形，采用随机种子，在该网络范围内创建了70个点以模拟用户和小基站的随机密集分布。其中，设定有20个为小蜂窝基站，50个为有接入需求的用户。此外，在区域的中心建立宏基站，按照宏基站和小基站的通信服务能力比例，设定宏基站的发射功率为50 dBm，小基站的发射功率为30 dBm，系统的总带宽为 10 MHz。具体的仿真实验环境参照文献[3-4]。同时，为了保证宏基站和小蜂窝基站基本参数的一致性，在仿真环境中忽略了信号传播过程的衰减和相互干扰。

图2分别给出了采用传统的用户资源分配策略和约束优化策略下，多用户的基站接入情况。显然，在优化之前，接入宏基站的用户数目远远多于接入小蜂窝基站的用户数目。必然导致宏基站的通信阻塞和小基站的资源浪费。相比较而言，通过约束函数进行优化后，更多的用户选择接入小蜂窝基站，而宏基站也能在保证频率的前提下服务一定数量的用户。宏基站和小基站之间的用户接入量没有再出现明显的失衡现象。

图3是各基站在优化前后的功率对比图。根据图像，在优化前，部分小基站功率为0，说明其没有工作是闲置的。在优化后，这部分闲置的小基站得到了充分利用，参与到用户的通信资源分配中，从而使得宏基站的输出功率得到降低。由此证明本文所设计的策略在一定程度上降低了宏基站的负载压力，并识别部分闲置小基站，把其通信资源合理的分配给周边的需求用户，从而整个通信网络的总体耗能降低。

图2 优化前后用户接入示意图[5]

图3 优化前后基站功率对比

3 结 语

本文从传统蜂窝网络的局限性出发，介绍了异构蜂窝网络的结构，并分析了其在多用户接入所面临的负载不均的问题。进而提出多约束函数的优化模型，以用户通信服务质量最优作为目标，将原问题的求解转换成类背包问题，按照贪婪思想进行启发式求解，最终获得满足约束条件的次优解。仿真结果表明，按照约束模型对随机分布的异构蜂窝网络优化后，能够在一定程度上调节宏基站和小基站在多用户接入时的负载不均问题，降低通信网络的总体耗能。