制导滤波器对导引头寄生回路特性影响分析*

许 琛,马清华,杨 凯,马 菲,王荔豪,韩 迪

(西安现代控制技术研究所, 西安 710065)

0 引言

导引头是导弹的核心组成部分,平台导引头能够对目标进行搜索、截获并跟踪[1]。为了保证制导精度,导引头稳定平台应具有良好的隔离效果以抗弹体姿态的扰动[2]。当隔离效果不达标时,在制导回路中会额外生成一条回路,称为隔离度寄生回路,对制导系统的稳定性带来不利影响[3],使平台导引头的性能受到严重损害。

众多学者对隔离度进行了深入研究:崔莹莹[4]等比较了两种不同的导引头模型,得出了基于绝对角速度建立导引头隔离度模型的结论；李富贵[5]等对视线角速率信号的不同提取点对寄生回路产生的影响进行了研究；徐平[6]等以末制导炮弹为对象,分析了隔离度对其制导精度产生的影响。但到目前为止,在隔离度寄生回路的研究中,很少有学者会关注制导滤波器对该回路稳定性造成的影响。

为了深入研究隔离度寄生回路稳定性的影响因素,文中建立了隔离度及寄生回路传递函数模型。并从导引参数、隔离度特性以及制导滤波器的差异这3个影响因素出发,对寄生回路的稳定性进行了深入分析。研究结果能够为导引头设计、制导控制系统方案制定以及参数的确定提供依据。

1 数学模型建立

1.1 隔离度模型

隔离度模型如图1所示,其中G1(s)为跟踪回路校正网络;G2(s)为稳定回路校正网络;H(s)为速率陀螺传函;GD(s)为干扰力矩传函,当干扰力矩为粘滞阻尼力矩时有GD(s)=kv,其中kv为粘滞阻尼力矩系数;k1、k2为增益系数;kT为力矩系数;kE反电势系数。

图1 平台导引头隔离度模型

由图1可得隔离度传递函数为:

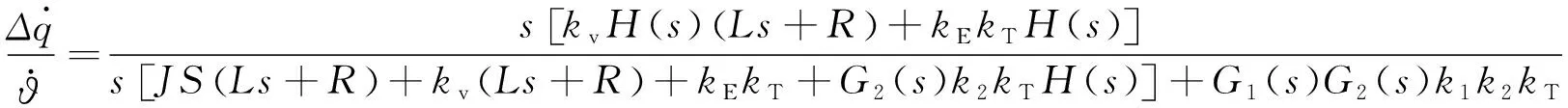
(1)

1.2 隔离度寄生回路模型

图2 包含隔离度寄生回路的制导回路简化模型

考虑隔离度回路为负反馈,隔离度寄生回路模型如图3所示。图中Glb(s)为制导滤波器传函;3阶自动驾驶仪模型中Tg为制导时间常数;Tα为攻角时间常数;N为比例导引系数;vm为导弹飞行速度;vc为弹目相对速度。

由图3可知寄生回路开环传函如下:

(2)

由式(2)可知,导引参数、隔离度以及制导滤波器均会对隔离度寄生回路特性产生影响。

2 寄生回路稳定性时域分析

(3)

选取一阶低通滤波器为制导滤波器,即Glb(s)=1/(Tbs+1)。应用Routh判据可得导引参数、隔离度幅值以及制导滤波器参数对寄生回路稳定区域的影响如图4、图5所示。

图4 制导参数、隔离度幅值对稳定区域的影响

图5 滤波器参数对稳定区域的影响

分析图4、图5可知,随着比例导引系数N、隔离度幅值R、弹目相对速度与导弹速度的比值vc/vm、攻角时间常数与制导时间常数的比值Tα/Tg的增加,隔离度寄生回路的稳定区域减小;而随着一阶低通滤波器参数Tb的增大,稳定区域会先减小后增大。可以看出,寄生回路的影响,迎击比尾追严重,高空比低空严重。为满足隔离度寄生回路稳定性要求,在确定导引参数时,制导时间常数Tg不能太小;在滤波器参数选取方面,以噪声频率为依据的同时,也要考虑其对稳定性的影响。

3 某毫米波平台导引头隔离度寄生回路稳定性影响分析

3.1 隔离度对寄生回路特性的影响

基于某毫米波平台导引头进行实例分析,选择导引头粘滞阻尼力矩作用下,隔离度分别为1%、3%、5%、7%的隔离度寄生回路传递函数进行分析,取N=4,vc=200 m/s,vm=200 m/s,Tg=0.2 s,Tα=2 s。图6为寄生回路开环伯德图。

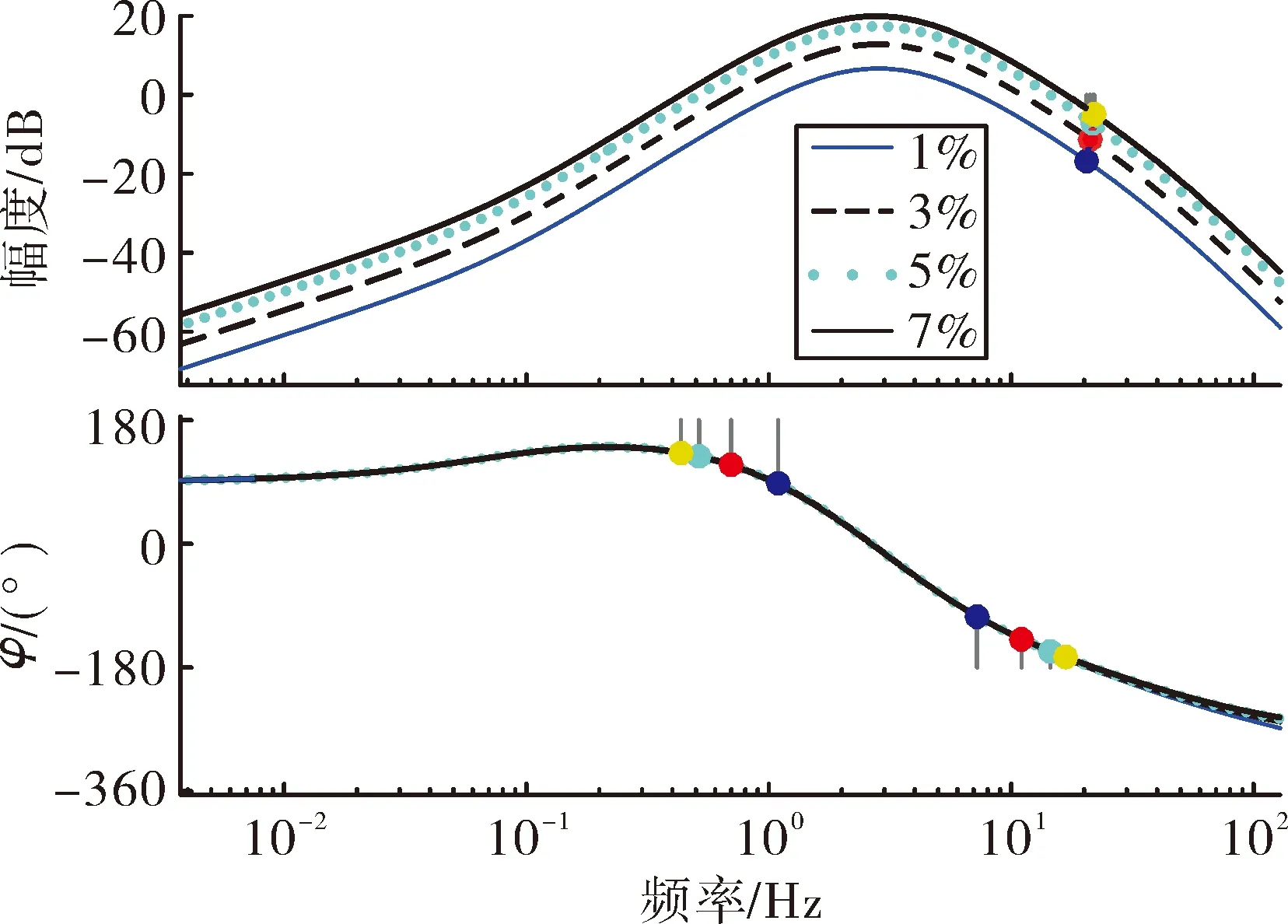
图6 隔离度寄生回路开环伯德图

由图6可得:随着隔离度增大,寄生回路的幅值增大,稳定性逐渐降低。隔离度寄生回路的稳定性在中频段最差。

凭借技术积累和工艺进步，上机数控以高性价比的产品和优质地服务赢得了众多下游实力客户的认可。协鑫集团、阿特斯、晶科能源、奥瑞德等国内主要光伏、蓝宝石厂商均与上机数控建立了长期稳定的合作关系。

3.2 滤波器对隔离度寄生回路的影响

以粘滞阻尼力矩作用下导引头隔离度为5%的隔离度寄生回路传函为研究对象,选取3种常用的制导滤波器:α、β、γ滤波器、Butterworth滤波器以及一阶低通滤波器。其中α、β、γ滤波器参数的选择遵循临界阻尼原则,Butterworth滤波器的阻尼系数为最佳阻尼比0.707。在3种滤波器带宽分别为10 Hz、0.5 Hz的条件下进行分析。图7给出了带宽相同时3种滤波器的伯德图,图8、图9给出了阻尼力矩条件下,在上述两个带宽处,各滤波器作用于寄生回路的伯德图。

由图7可知:在带宽相同的情况下,Butterworth滤波器对高频噪声的衰减最大;一阶低通滤波器其次；α、β、γ滤波器对高频噪声抑制能力最小；但α、β、γ滤波器造成的相位滞后最小；一阶低通滤波器其次,Butterworth滤波器对低频段造成的相位滞后是最大的。而低频段的相位滞后会降低系统的稳定性。

图7 带宽相同时3种滤波器伯德图

图8 滤波器带宽10 Hz寄生回路伯德图

图9 滤波器带宽0.5 Hz寄生回路伯德图

分析图8、图9可以发现,由于寄生回路稳定性最严峻的区域位于10 Hz附近,因此当滤波器带宽取10 Hz时,滤波器在该频段造成的相角滞后过多,而幅值衰减过少,从而导致原本稳定的系统失稳;而当滤波器带宽为0.5 Hz时,在其影响下,寄生回路在10 Hz处幅值明显减小,这使得截止频率降低,闭环系统响应速度有所下降,但系统具有更好的稳定性。

当滤波器带宽取在系统稳定性最严峻的10 Hz附近时,由于Butterworth滤波器使得系统相角减小过多,导致系统失稳;而α、β、γ滤波器与一阶低通滤波器在10 Hz附近对系统影响较为缓和,对闭环稳定性产生的不利影响较Butterworth滤波器小;当滤波器带宽取0.5 Hz时,由于距10 Hz频率较远,在滤波器作用下,系统幅值在低频段处就开始下降,此时Butterworth滤波器对系统的稳定性提高最为明显。

因此,在选择制导滤波器种类以及带宽时,以噪声频率特点为依据的同时,还需考虑对导引头隔离度寄生回路稳定性的影响。应分析出寄生回路稳定性最严峻的频段,选择滤波器带宽尽量低于该频段,选择Butterworth滤波器对系统稳定性提高最明显;当滤波器的带宽与稳定性严峻的频段较为接近时,选择α、β、γ滤波器与一阶低通滤波器对寄生回路稳定性造成的不利影响较小。

4 结论

建立了平台导引头隔离度及其引起的寄生回路模型,详细分析了导引参数、隔离度幅值以及制导滤波器参数3部分对寄生回路稳定性产生的影响,得到结论如下:

1)随着比例导引系数N、隔离度幅值R、弹目相对速度与导弹速度的比值vc/vm、攻角时间常数与制导时间常数的比值Tα/Tg的增加,隔离度寄生回路的稳定性恶化;

2)寄生回路稳定性最严峻的频段位于中频段,选择滤波器带宽尽量低于该频段,此时选择Butterworth滤波器对系统稳定性提高最明显;当滤波器带宽接近稳定性最严峻的频段时,选择α、β、γ滤波器与一阶低通滤波器对寄生回路稳定性造成的不利影响最小。