基于循环神经网络的金融数据预测系统
黄有为 高燕
摘 要:金融预测旨在对金融历史数据进行分析,构建预测模型,并对未来数据走势作出预测。系统创新性地将最新的深度学习成果与金融预测相结合,提出使用循环神经网络预测金融数据变化的方法。首先介绍了近几年人工智能的突破性成果,以RNN相关技术为基础对系统进行设计,然后通过实验组展示系统预测效果,并对系统获得的结果数据,使用深度学习相关评估算法评估其预测准确性。实验评估结果表明,使用循环神经网络学习与分析历史数据,并将其模型用于预测未来金融数据走势的方案具有较高的可靠性与准确性。因此,深度学习在金融预测领域具有较大发展潜力。
关键词:深度学习;神经网络;RNN;大数据;金融预测
DOI:10. 11907/rjdk. 181779
中图分类号:TP303文献标识码:A文章编号:1672-7800(2019)001-0028-06
Abstract: The purpose of financial forecasting is to analyze financial historical data, construct forecasting model, and forecast the trend of future data. This paper combines the latest in-depth learning results with financial forecasting systematically and creatively, and puts forward a method of forecasting the changes of financial data using cyclic neural network. Firstly, this paper introduces the breakthrough of artificial intelligence in recent years, designs the system based on RNN technology, realizes it by computer language, and then displays the predictive effect of the system through the experimental group, and evaluates the predictive accuracy of the system by depth learning related evaluation algorithm. According to the final experimental evaluation results, the scheme uses the cyclic neural network to learn and analyze historical data, and using the model to predict the future trend of financial data has certain reliability and accuracy, thus in-depth learning has development potential in financial forecasting.
Key Words: deep learning; neural network; RNN; big data; financial forecast
0 引言
人工智能的概念早在1956年即被提出,经历了半个多世纪的发展,直至人工神经网络理论的提出,以及Google第一次发表深度学习技术,并通过“人机大战”[1]的形式走进公众视野,人们才真正认识到深度学习的强大能力。
关于人工智能的发展,传统人工智能技术在上世纪70-90年代占据了绝对领导地位,例如非线性与线性核 SVM、贝叶斯分类器等方法,被认为适合于小型数据计算。随着互联网的迅速发展,Internet中的信息产生爆炸式增长。以金融数据为例,对新浪财经进行数据爬虫,仅期货一个板块即获得了几十万条数据,而且该数字每时每刻还在不断增长。因此,近几年提出“大数据”概念,以研究互联网中产生的庞大数据量,并对其加以利用[2]。然而,类似金融领域的相关“大数据”已无法通过人工进行分析、挖掘或预测,即使借助传统人工智能或统计软件的帮助,想要拟合出数据变化特征也十分困难。因为人工建立的模型存在效率与容错率低、扩展与升级缓慢等问题,且传统人工智能方法并不适用于对庞大数据的特征挖掘。
深度学习不同于传统人工智能方法[3],其采用“逆向推导思维”方式,以庞大的数据量为基础,借助神经网络自主学习的特點(神经元构建连接关系的过程),通过反复学习历史数据进行不断改进与优化,拟合出一个最优模型,其中RNN(循环神经网络)适合于时间序列上数据特征的学习。由于金融数据具有序列性,可通过RNN拟合出历史数据特征作为预测模型,并在预测过程中对模型不断进行优化。随着数据量的累积,模型理论上可无限趋于最优。
金融预测方法在国际上得到了广泛关注,诺贝尔经济学奖曾分别于2003年与2011年颁发给成功将基于自回归条件差异及向量自回归预测模型应用于金融时间序列预测的两位经济学家[4]。
在不同学术领域,学者们提出多种金融分析预测方法,包括:①基于经济学的金融预测学及其改进的预测方法,例如基于灰色线性回归组合模型的金融预测方法,其具有数据需求量少、预测模型精确的特点[5];②基于数学与统计学的预测方法与模型,例如改进的隐马尔科夫模型及其在金融预测中的应用[6-7]、基于贝叶斯最大似然估计的金融预测等[8]。近几年又出现了结合计算机技术对金融数据进行分析与预测的方法,其中以深度学习为基础的金融预测技术发展尤为迅速[9],例如基于遗传算法与神经网络耦合的金融预测方法[10]、FEPA模型[11]、广义回归神经网络的金融预测模型[12]等。此外,也不乏对计算机技术中传统预测方法的应用,例如SVM方法[13]、EMD方法[14]等。在与计算机结合的金融分析预测方法中,无论是传统预测方法,还是基于卷积神经网络的深度学习金融预测方法,都具有较强的创新性,且在特定领域或环境下具有较高的准确性与可靠性。
综合上述结合经济学、数学、计算机科学针对金融数据的分析方案,即使是基于CNN(卷积神经网络)或传统人工智能的预测方法,如果是在长时间序列的历史数据上构建模型,该模型对数据时间前后依赖性关系的记忆与分析能力较差,无法满足长序列上的金融数据分析要求。本系统创新性地采用RNN(循环神经网络)中的LSTM(长短期记忆神经网络)[15]构建金融预测模型,其特点为:预测模型是针对历史数据在时间线上相互影响产生的变化特征进行拟合,而非数据本身,即当日数据变化与昨日数据相关,昨日与前日数据相关,前日又与更久远的数据相关,以此类推分析其递归关系,并且所追踪的数据序列更长。该方法充分利用了金融数据变化的时间序列性、关联性及重演性等特点。
1 系统设计
RNN(循环神经网络)模型设计过程包括:数据加载、模型构建、数据训练以及评估模型设计。
1.1 数据加载
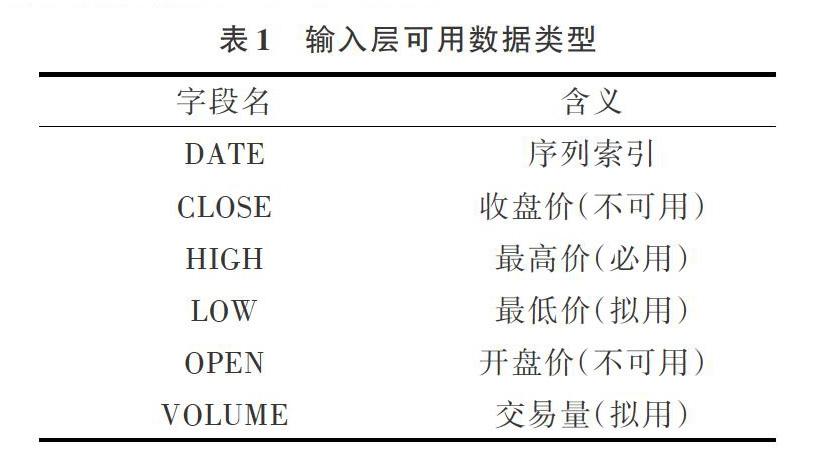
(1)数据类型:金融数据。例如,期货和股票通常提供以下4个价格:最高价、最低价、开盘价、收盘价。由于最高价和最低价已包含开盘价与收盘价,又因为开盘价和收盘价是某天数据中偶然出现的价格,故训练数据应选择最高价或最低价作为输入数据。实验为了加速数据训练过程,将输入数据类型暂时设定为最高价。
(2)数据窗口:对应RNN中的滑动窗口(为了预测目标数据所需输入的特征数据序列,是一段长度可变、数据量有限、数据性质相同的连续数据,可理解为数学中的离散数据区间,例如:数据1、2、3、4、5可作为一个窗口,滑动到下一个窗口则为2、3、4、5、6)。该窗口大小需要根据RNN实际学习得出的模型进行调整。理论上,若窗口过大,随着时间推移,数据变化特征对市场随机噪点越敏感,距离预测目标值过于遥远的数据对目标的意义则越小;若窗口过小,将导致深度学习产生过拟合,预测结果没有实际参考价值。
可加载数据类型如表1所示。
1.2 模型构建
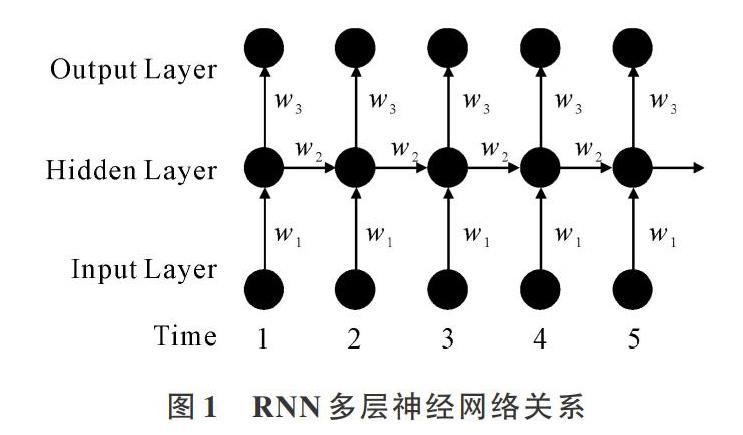
RNN包括输入层(Input Layer)、输出层(Output Layer)及隐藏层(Hidden Layer),其特点是每层都有时间反馈循环,并且层之间由叠加构成[16],其网络结构如图1所示。
由图1可知,神经网络结构设计如下:设日期(序列号)为t,价格为P[t],模型分3步预测P[t+w]。滑动窗口P[t…t+w-1],其中t∈(1,tmax-w+1),且t∈N,w为设定窗口大小,P矩阵作为输入层输入矩阵,记作INPUT(T)。连接上次隐藏层HIDE(T-1),生成当前隐藏层的HIDE(T),将预测值P[t+w]作为输出层的输入,输出预测结果,记作OUTPUT(T)。
Dropout设计:深度学习过程中,过度拟合是一个严重问题,Dropout是解决该问题的一种技术,其关键思想是在训练过程中从神经网络中随机地丢弃单元(连同其连接)[17]。金融数据,尤其是期货和股票受到市场环境影响,存在暴涨暴跌的可能性,因此需要为输出层添加Dropout函数,以去除巨大价格波动造成的影响。同时由于RNN中的循环会放大噪声,扰乱学习过程,故将Dropout用于非循环连接。
1.3 训练与评估方案
将1.2节中已构建的RNN神经网络模型设为LSTM(),使用LSTM()进行数据预测训练并给出模型评估方案,具体步骤如下:
(1)对训练数据组与测试数据组进行数据分离。
(2)将分离的数据组再分别分离为窗口与目标。
(3)配置训练超参数,包括学习率、循环次数与batch批次。
(4)设计优化方案,定义损失函数与优化器,其中优化器采用Adam。损失函数公式为:
(5)对LSTM(窗口数组、目标值、训练次数、批次)进行训练。
(6)对测试数据组中实际值与LSTM()给出的预测值采用评估算法进行误差评估,误差越低表示模型越优良。
(7)保存模型文件。
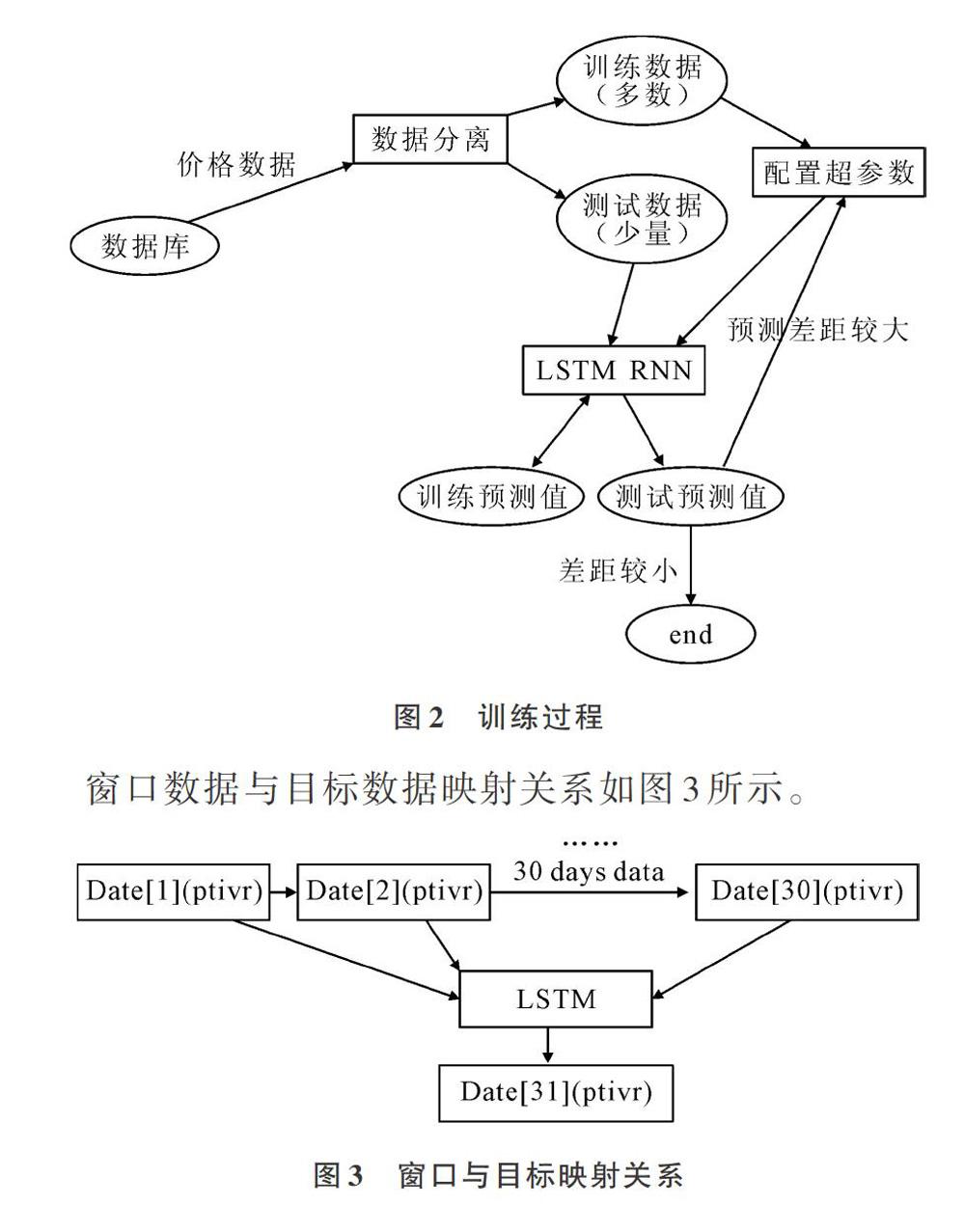
训练过程设计如图2所示,图中训练预测值与LSTM RNN表示训练过程中的自优化操作,将自身训练产生的预测值回收后,执行步骤(4)进行方案优化。
2 关键技术
2.1 预测技术可行性
金融学预测技术满足可行性需要的3个假定前提为:①市场行为消化一切行为;②价格会以趋势的形式演变;③历史终会重演[18]。满足上述条件方可对金融预测进行研究。
2.2 LSTM技术
LSTM(长短期记忆网络)是在RNN基础上,为了解决长序数据建模存在的依赖性记忆下降问题而提出的一种改进算法,在LSTM中引入Cell,并将其封装在block中,每一块block包含了输入门、遗忘门、输出门与Cell[19],其作用是防止对序列中久远节点的遗忘,增加NN的深度。LSTM block结构如图4所示。
由于金融分析具有数据量庞大、数据变化快、窗口大、滑动范围广(指在训练模型过程中所需输入的数据段较多且区间较长)等特点,因此需要使用LSTM技术进行数据训练,而非传统的RNN。
2.3 数据可视化技术
针对神经网络训练过程制作可视化图形,采用线性图分别表现原始数据、训练预测数据与测试预测数据,实验使用 Python Data Analysis Library——Pandas进行数据分析,或通过Web技术将数据可视化至浏览器的Canvas中。
2.4 数据爬虫技术
循环神经网络的模型训练是无限的,互聯网金融每日会产生新的商品价格、交易量等数据,系统需要定期更新数据库中的历史数据,以达到更好的预测效果。本文通过Python、Node.js等工具语言实现爬虫算法,并提供可视化的爬虫管理与数据管理功能,负责数据的获取、整理与存储。
3 核心算法
基于RNN的神经网络实现需要对从互联网爬取的数据进行加载,并去除无效数据。训练前需要对训练数据与仿真预测数据,以及训练过程中的窗口数据与预测目标数据进行分离。其中,窗口数据为二维数组,目标数据为一维数组,在评估模型阶段对目标数组与预测数组进行对比,给出评估结果。
3.1 最优爬虫算法
爬虫模块采用最优爬虫算法,即要求只可爬取规定范围内的商品数据,从而使冗余数据量达到最少。假定已对数据类型、数据量进行了规范,使用最优爬虫算法筛选出指定商品、商品属性及其数据类型,并进行爬取与存储,以下为实现该算法的关键代码:
3.2 增量式爬虫策略
爬虫模块采用增量式爬虫,要求不能爬取重复数据,故需要对爬虫系统实行重新访问策略,并且是增量式而非重置模式。要实现增量式需要实现数据比对功能,实现该功能关键代码如下:
3.3 LSTM神经网络算法
在2.2节中已介绍LSTM是一种门限类型的RNN改进算法,并给出了block(下称节点)结构图,其节点包括输入门、输出门与遗忘门,可使自循环权重发生变化。在模型参数固定的情况下,不同时刻的积分尺寸可以动态改变,从而避免了梯度消失或梯度爆炸问题。LSTM单元(Cell)中包含的计算公式如下:
其中公式(2)为遗忘门限计算公式,公式(3)表示输入门限计算公式,公式(4)为前一个Cell状态计算公式,公式(5)表示当前Cell状态计算公式,公式(6)为输出门限计算公式,公式(7)表示当前单元最终输出结果计算公式。所有公式被封装在LSTM节点中,系统传入的金融数据经过节点时将采用相关公式进行计算。根据窗口大小及数量,在时间序列上产生多个对应的Cell状态,且前一状态可影响下一狀态。其中公式中的tanh为激活函数。
激活函数:非线性函数,将输出值作非线性变化,然后输出到下一层。
通过对多组数据进行多组训练,使节点之间的W、b变量达到最优,该过程需要通过成本函数实现。
成本函数:定量评估特定输入值,计算该值与真实值的差距,以此调整层之间的权重,减少损失值。该过程称为反向传递,损失值越小,结果越准确[20]。
3.4 数据加载实现
神经网络的“数据加载”是指对数据库进行读取与整理,具体步骤为:引入驱动,加载数据库配置文件,获取指定商品价格,去除干扰数据(未交易价格),以float32形式暂存于数组中。
3.5 窗口与目标数据分离算法
训练实现要求从SQL获取到的数组数据中分离出窗口数据与目标数据,具体算法如下:
定义函数:窗口分离(数据集, 窗口大小):
窗口数组, 目标数组 = 数组[][], 数组[];
循环(次数:数据长度 - 窗口大小):
窗口数组增加(数据集[循环次数] 至 数据集[循环次数+窗口大小]);
目标数组增加(数据集[循环次数 + 窗口大小 + 1]);
循环结束;
返回 窗口数据数组,目标数据数组;
3.6 训练与测试数据分离算法
为了进行实验比较,下面对测试数据与训练数据进行分离,具体算法如下:
定义常量:训练数据百分比;
定义:训练数据长度 = 数据集长度 × 训练数据百分比
测试数据长度 = 数据集长度 - 训练数据长度
训练数组,测试数组 = 数据集[起始位置 至 训练数据长度],数据集[训练数组长度 至 数据集长度]
定义常量:窗口大小 (系统采用30天)
训练窗口数组, 训练目标数组 = 窗口分离(训练数组, 窗口大小)
测试窗口数组, 测试目标数组 = 窗口分离(测试数组, 窗口大小)
3.7 LSTM数据训练算法
对上述输入数据进行矩阵变换,LSTM对输入矩阵格式的构造方法如下:
训练数据 = 格式化(训练窗口数据, 训练窗口数据长度, 1, 窗口大小)
数据训练具体函数与算法如下:
定义函数:LSTM(训练数据,目标数据,循环次数,批次);
定义变量:输入权值;
定义变量:输入偏置;
输入运算 = 训练数据*输入权值+输入偏置;
创建LSTM神经元(数目);
初始化零值(批次);
输出数据 = 接收张量;
定义变量:输出权值;
定义变量:输出偏置;
预测值 = 输出数据*输出权值+输出偏置;
DROPOUT();
返回 预测值;
3.8 模型评估算法
训练完成后对模型进行评估与改进,其评估算法如下:
训练预测数组 = LSTM()=>预测(训练窗口数组);
测试预测数组 = LSTM()=>预测(测试窗口数组);
格式化数据(训练预测数组,测试预测数组);
训练数据评估 = [(训练预测数据-训练目标数据)2预测次数];
测试数据评估 = [(测试预测数据-测试目标数据)2预测次数];
打印(训练数据评估,测试数据评估);
可视化;
4 算法改进实验
本文对算法中的不同超参数进行调整,并进行了多组实验,通过对比实验对算法进行改进。
4.1 训练次数对照实验组
4.2 滑动窗口对照实验组
LSTM中若滑动窗口过大将导致预测准确率下降,原因是距离过于遥远的数据产生噪点过多,与目标数据的映射关系较小,并且窗口过大会导致可训练的窗口批次过少,训练量不足,从而产生过拟合问题。但若滑动窗口过小,数据之间在时间序列上关联性降低,也将导致训练过拟合问题,预测曲线过于贴合目标数据曲线,令预测结果没有实际参考价值。图9-图11分别表示滑动窗口为100天、1天、30天的预测结果(彩图见封底)。
实验结果显示,以100天为滑动窗口,预测效果明显下降;以30天为滑动窗口,预测结果有一定参考价值;以1天为滑动窗口,预测数据几乎重合于实际目标数据,产生预测过拟合问题,使预测数据没有实际参考价值。得出结论,以30天为滑动窗口預测下一天价格较为合适,预测走势曲线与真实曲线基本接近,差价较低,具有一定参考价值。
5 结语
本文研究使用RNN构建与训练金融大数据预测模型,实验以30天为滑动窗口,预测第31天的价格,训练次数为100次,训练数据量为60%,对不同金融商品进行单独训练,生成训练记忆文件。经过评估算法检测,部分商品的预测值接近目标值。例如:黄金预测模型评估值(平均差价)为2~5元,该价格较为合适,但目前仍有部分商品评估值(平均差价)高达100~1 000元,因而缺乏参考性。未来考虑针对不同商品的不同特性与数据量单独调整超参数,或引入更多输入参数,例如交易量、商品交易数据、相关行业数据等,这类数据会对商品价格走势造成影响,能够进一步提高预测准确性。
参考文献:
[1] 李颢维. 人机大战与人工智能的未来发展[J]. 考试周刊,2018(40):192-193.
[2] 杨柳. 互联网时代下的大数据的统筹[J]. 中国战略新兴产业,2018(20):112.
[3] 董鑫. 未来人工智能自主学习网络的构建[J]. 电子技术与软件工程,2018(3):252.
[4] 张贵勇. 改进的卷积神经网络在金融预测中的应用研究[D]. 郑州:郑州大学,2016.
[5] 卢阳. 基于灰色线性回归组合模型的金融预测方法[J]. 统计与决策,2017(10):91-93.
[6] 何剑. 风险管理和金融预测中的统计方法应用[J]. 商场现代化,2006(32):368-369.
[7] 徐朱佳,谢锐,刘嘉,等. 隐马尔科夫模型的改进及其在金融预测中的应用[J]. 工程数学学报,2017,34(5):469-478.
[8] 沈斌,温涛. 基于贝叶斯最大似然估计的金融预测[J]. 统计与决策,2018,34(7):85-88.
[9] 周飞燕,金林鹏,董军. 卷积神经网络研究综述[J]. 计算机学报,2017,40(6):1229-1251.
[10] 宋晓勇,陈年生. 遗传算法和神经网络耦合的金融预测系统[J]. 上海交通大学学报,2016,50(2):313-316.
[11] 张承钊. 一种金融市场预测的深度学习模型:FEPA模型[D]. 成都:电子科技大学,2016.
[12] 廖薇,冯小兵,曹伟莹,等. 广义回归神经网络的金融预测模型研究[J]. 商业时代,2010(7):42-43.
[13] 李祥飞,张再生. 基于误差同步预测的SVM金融时间序列预测方法[J]. 天津大学学报:自然科学与工程技术版,2014,47(1):86-94.
[14] 王方. 基于EMD和STSA的金融波动研究[D]. 天津:天津大学,2016.
[15] 朱星嘉,李红莲,吕学强,等. 一种改进的Attention-Based LSTM特征选择模型[J]. 北京信息科技大学学报:自然科学版,2018,33(2):54-59.
[16] 杨祎玥,伏潜,万定生. 基于深度循环神经网络的时间序列预测模型[J]. 计算机技术与发展,2017,27(3):35-38,43.
[17] SRIVASTAVA N, HINTON G, KRIZHEVSKY A, et al. Dropout: a simple way to prevent neural networks from overfitting[J]. Journal of Machine Learning Research, 2014, 15(1):1929-1958.
[18] 黄圣根. 期货投资技术分析[J]. 资本市场, 2013(6):126-127.
[19] 唐寅. 长短时记忆神经网络模型改进[J]. 时代金融, 2016(24):281-282.
[20] 李嘉璇. TensorFlow技术解析与实战[M]. 北京:人民邮电出版社,2017.
(责任编辑:黄 健)

