地铁盾构管片姿态的水平偏差算法研究

黄志伟，王克荣，龚 率，乔燕燕，蒲星钢

(1.成都市勘察测绘研究院，四川 成都 610081;2.成都西汇市政规划设计有限公司，四川 成都 611700，3.四川水利职业技术学院，四川 成都 611231)

随着多个城市掀起地铁轨道交通建设热潮，盾构施工以其环保、高效、安全等优势被建设和施工单位广泛的应用[1]。盾构掘进过程中，刚拼接装的管片受注浆加固、盾构机实时姿态误差及地质条件的影响，经常发生管片位移现象，若忽视盾构掘进中成型管片姿态的重要性，没有及时发现掘进偏差并加以有效纠偏的话，容易发生成洞隧道偏离设计轴线较大的质量事故，轻者修改设计进行调线调坡，重者二次改造，这势必会对业主方与施工方造成无法挽回的损失与影响[2]。《成都地铁工程施工测量管理细则》关于管片姿态偏差，警情等级划分黄((50，100] mm)、橙((100，150]mm)、红(大于150 mm)3类，并规定对应的处置要求。为了控制管片位移超限，提高控制测量精度的同时，通过每天的管片姿态测量，实测出管片的位移趋势，及时采取措施尽量减小位移量，并起到复核盾构导向系统的作用[3]。管片姿态的测量频率高，重复作业量大，尤其是水平偏差，控制难度大，计算较为复杂。传统的方法通常将管片姿态测量点的实测坐标展点至AUTOCAD线路平面图中，量取各点到线路设计中线的垂线距离，然后根据设计文件信息进行计算得到水平偏差值及里程。该方法人工干预大、内业耗时，而且容易出现多值性情况。本文介绍一种利用平面线形设计参数、隧道中线与线路中线偏差、长短链等设计文件自动计算管片姿态处对应水平偏差及里程的方法，并通过程序实现对地铁线路的管片姿态水平偏差的计算，以验证数学模型的正确性及实用性。

1 盾构管片姿态的测量方法

结合盾构机的掘进进度，施工单位、监理、第三方测量需要按照要求进行管片姿态的测量，管片姿态测量的目的是获得待测环管片环心的平面坐标和高程值，进而与设计值比较计算出偏差值。测量方法一般采用极坐标测量或者自由设站法，具体操作流程一般是先将铝合金管尺水平放置在待测的某一环管片上，且铝合金管尺与环缝对齐，再将水平尺放在铝合金管尺的中央，将铝合金管尺调平。此时贴在铝合金管尺中点处的反射片原则上就与待测环管片的中心在同一铅垂线上，待测环管片中心平面坐标即反射片坐标[4]。环管片中心的高程值可通过三角高程得到反射片中心高程值或者几何水准测量管尺处的顶、底板高程并结合管片结构间接得到，如图1所示。

图1 管片姿态的测量示意

2 管片姿态测量点的水平位移偏差的计算

结合线路的平面线形设计文件，先通过分析与5桩点的距离和方向判断测量点在线路中的具体位置[5]，然后推导出姿态测量点在直线段、圆曲线段及缓和曲线段对应里程和水平偏差的数学模型，最后根据隧线中线关系及长短链进行里程与偏差的改正。

2.1 隧道施工中线与线路设计中线的关系

管片姿态测量点的水平偏差是测点与隧道施工中线的差值，需知道隧道施工中线与线路设计中线的关系，以便进行偏差的计算。在直线段，隧道中线与线路中线重合。在曲线段，地铁运行受超高的影响，车体向曲线内侧倾斜，从而曲线段隧道断面内尺寸加大。为了减少曲线隧道开挖断面工程量降低成本，设计单位将设计中线向曲线内侧偏移某一个量Mv，圆曲线的偏移量大小都等于Mv，隧道中线偏移量应在缓和曲线范围内平顺变化，任意里程的偏移量与该点到直缓点(缓直点)的曲线长成比例[6]。

2.2 姿态测量点在直线段水平偏差及里程的计算方法

设管片姿态测量点P(XP,YP)，点P对应线路中线点P0,所求的水平偏差为d，对应线路中线的里程为k。直缓点或缓直点的坐标为(X0，Y0)，过该点直线段的坐标方位角为A0，则该段直线的点斜式方程为：

Y-Y0=K1(X-X0).

(1)

式中：K1为直线的斜率，K1=tanA0。

过P，P0两点的直线的点斜式方程为：

Y-YP=K2(X-XP).

(2)

由于点P0是点P到线路中线的最近点，故两条直线互相垂直，K1×K2=-1。联合求解式(1)和式(2)，解得的未知数X，Y就是所求点P0的坐标，进而求得点P与点P0之间的距离即为水平偏差d和P0的里程。若该测段有长短链则进行里程改正。

2.3 姿态测量点在圆曲线段水平偏差及里程的计算方法

如果点P在曲线段，则需要判断P点在缓和曲线段内还是圆曲线段内。首先通过桩点及交点进行坐标转换建立曲线独立坐标系[7]，如图2所示。设圆心O坐标为(Xo,Yo)，可得到点O坐标的式为[8]：

(3)

式中：m为缓和曲线的切垂距；l0为缓和曲线总长度；p为圆曲线内移量；R为半径。

计算圆心O与点P的方位角后，得到点P所对应的切线角θ，如果θ大于缓和曲线的切线角β0，则说明点P在圆曲线区域内，否则点P在缓和曲线内。若点P在圆曲线区域内，由圆弧的弧长公式可知，从直缓点到点P0的曲线长l式为：

l=l0+(θ-β0)×R.

(4)

得到点P0的坐标(Xp0，Yp0)，其式为：

(5)

点P的水平偏差d为点P与P0之间的距离与偏移量Mv之差。点P的对应里程k为点P0里程。

图2 线路曲线独立坐标系示意

2.4 姿态测量点在缓和曲线段水平偏差及里程的计算方法

若任意点P在缓和曲线区域内，如图2所示。由参考文献[8]可以查得缓和曲线关于x，y的方程式，函数f(x,y)的参数方程为：

(6)

式中：l为缓和曲线上任意一点到直缓点的曲线长。

则点P(Xp,Yp)到缓和曲线上任意一点距离的平方，可以表示为：

(7)

关于l一阶导数为：

(8)

对l进行求导：

(9)

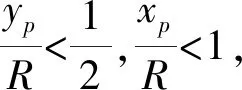
3 工程应用

为验证本文推导管片姿态测量点对应水平偏差与里程计算式的正确性与可行性，选取成都市在建地铁盾构区间的实测管片姿态数据进行分析。该盾构区间平面线形的部分线路设计文件如表1所示，该段的断链情况为短链：K35+497.425=K35+500.000-2.575 m。根据上文所述的数学模型进行程序的编写及自动计算，传统方法采用准确可靠的Autocad与Excel人工量算方法，两种方法的对比结果如表2所示。

从表2中计算结果可以看出，计算得到的管片姿态测量点在直线段、圆曲线段及缓和曲线段的水平偏差与传统方法比较，计算结果是一致的，验证数据模型的正确性，可应用于测量点水平偏差的批量计算。

表1 某地铁盾构区间平面线形的部分线路设计文件 m

注：表中R为圆曲线半径；L为缓和曲线长度

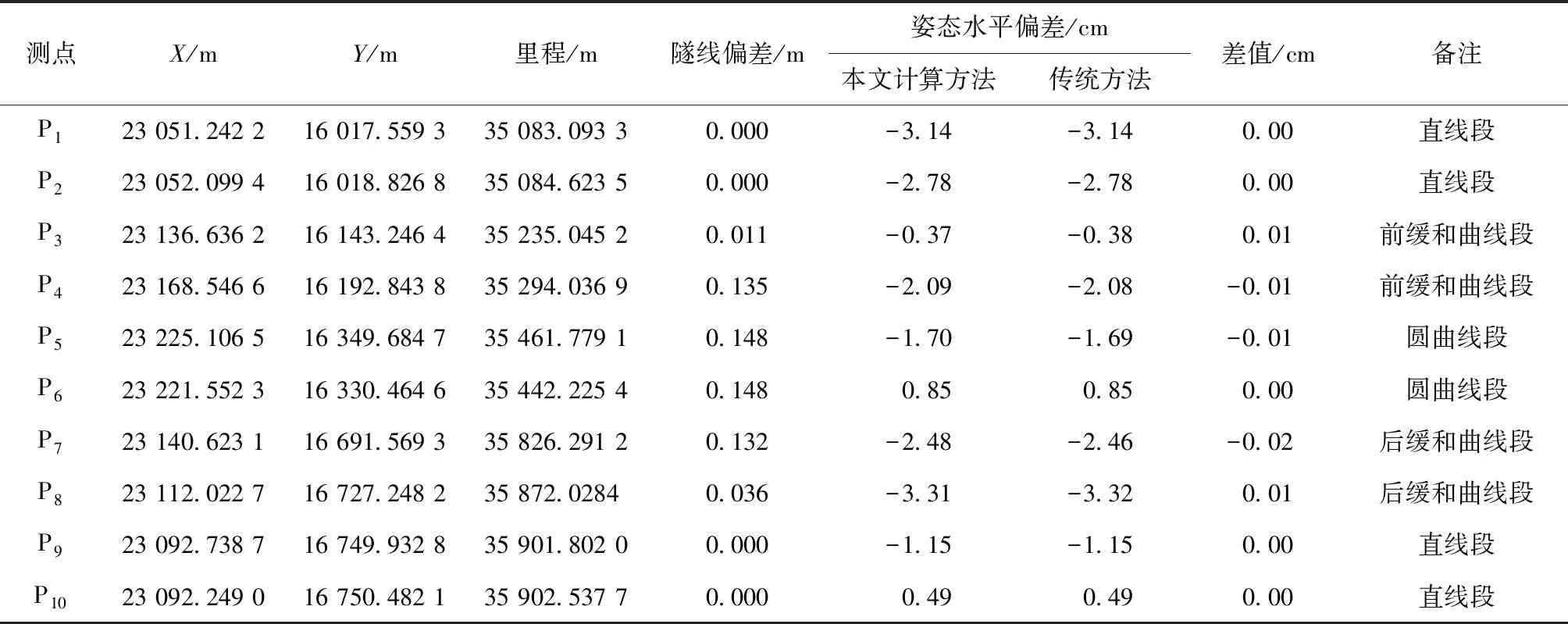
表2 部分实测管片姿态测点的水平偏差计算及对比结果

4 结束语

1)结合线路设计文件，可将管片姿态测量点的自动定位并完成对应里程及水平偏差的计算，并通过隧线中线偏差、长短链等信息完成姿态测量点的偏差与里程的改正。

2)对管片姿态测量点在直线段、圆曲线段及缓和曲线段水平偏差计算的数学模型进行推导，结合算例，验证其数学模型的正确性。

3)该方法可准确、高效地完成管片姿态的水平偏差的计算，同时可拓展应用于地铁盾构断面测量的批量计算。