加权叠加结构滤波器组动态信道化结构研究*

马 宏，张 超，焦义文



加权叠加结构滤波器组动态信道化结构研究*

马 宏，张 超，焦义文

（中国人民解放军航天工程大学 北京 101416）

针对传统DFT多相结构滤波器组动态信道化结构要求系统过采样因子必须为整数，限制了参数设置的灵活性的问题，将灵活高效的加权叠加（WOLA）结构滤波器组引入动态信道化结构。通过公式推导得到WOLA综合滤波器组的实现结构，进而设计了基于WOLA结构滤波器组的动态信道化结构。仿真结果表明，设计的动态信道化结构解除了系统过采样因子必须为整数的限制，增强了参数设置的灵活性，同时与DFT多相结构滤波器组动态信道化结构相比，重构误差减小了一个量级，具有良好的重构特性。

动态信道化；加权叠加（WOLA）结构；灵活性；重构误差

引 言

在信息化战争中，信息权是双方争夺的焦点，通过信号侦察可以对空间内存在的信号进行接收和分析，获取有价值的信息，为后续的决策提供情报支援[1]。随着通信技术的不断发展，空间电磁环境与通信环境日益复杂，主要表现为在接收时域、频域和空域中存在高度密集的信号，接收带宽越来越宽，信号的调制方式和参数复杂多变[2]，这些都给信号侦察带来了巨大的挑战。动态信道化技术最早由李冰提出[3]，利用分析滤波器组将接收带宽分为若干个信道，再根据能量检测的结果动态配置综合滤波器组的输入，进行信号重构，实现动态变化情况下的信号侦察，能够满足未来空间电磁环境对信号侦察的需求。而后李冰又研究了基于非均匀滤波器组的动态信道化技术[4]，简化了动态信道化的系统设计，提高了运算效率。2016年国防科技大学胡君朋将信道化技术实现结构的直接型和间接型结构的优点综合起来，提出了一种混合结构的动态信道化技术[5]。当前所研究的动态信道化技术均是基于DFT多相结构滤波器组[5]，该结构能够降低系统运算量，但是要求系统的过采样因子，即信道数与抽取倍数的比值为整数，限制了参数设置的灵活性。同时美国的JPL在2012年经过大量实验指出[6]，当系统的过采样因子OS的取值范围在1.2~1.5之间时，重构性能最优，因此DFT多相结构滤波器组动态信道化结构并不是最优的选择。

针对该问题，本文提出一种基于加权叠加结构滤波器组的动态信道化结构，将高效灵活的加权叠加滤波器组引入动态信道化设计中，在能够动态接收提取带宽内存在的信号的同时，解除了系统过采样因子必须为整数的限制，提高了系统的重构性能。

1 动态信道化结构数学模型

动态信道化结构的核心是滤波器组。复指数调制滤波器组是最原始的滤波器组[7]，目前应用于动态信道化结构中的DFT多相结构滤波器组是其高效实现结构，两者特性相同，因此本节以复指数调制滤波器组为例，讨论动态信道化结构的数学模型。其结构图如图1所示。

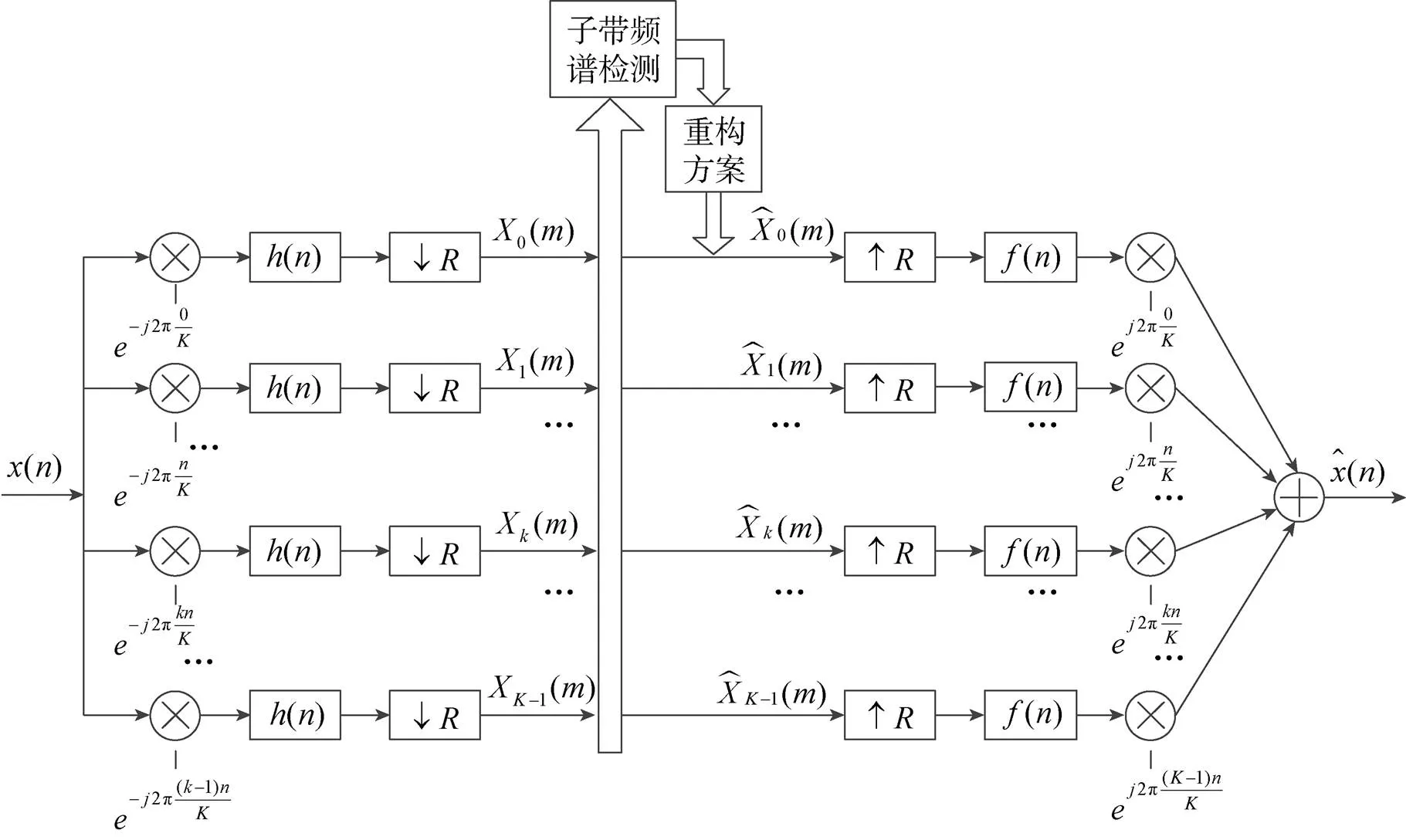
图1 复指数调制滤波器组动态信道化结构

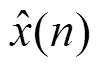
首先，接收带宽经过分析滤波器组后被分割成若干个信道，其中包含的多个信号也随之分散于各个信道中。需要注意的是，若信号带宽大于信道带宽或者信号处于两个信道的交界处，则信号频谱会被信道割裂，使得信号跨信道输出，造成失真。然后利用能量检测法对各个信道进行检测，判断信号在各个信道内的分布。最后根据能量检测的结果，使存在信号的信道数据保持不变，其余信道全部置零，作为综合滤波器组的输入，进行重构，从而提取信号。当接收带宽内信号的状态及参数动态变化时，依据能量检测的结果，动态调整综合滤波器组的输入数据，从而实现动态接收、提取。

2 加权叠加结构滤波器组研究

WOLA结构滤波器组是一种高效灵活的滤波器组，能够解除系统过采样因子必须为整数的限制[9]。文献[9]对加权叠加结构滤波器组的信道化过程进行了分析，而对于利用加权叠加结构滤波器组实现信号重构的过程并未展开研究。本节对加权叠加结构滤波器组进行研究，重点分析加权叠加结构综合滤波器组，推导出其实现结构，为后续动态信道化结构设计奠定基础。

2.1 加权叠加结构分析滤波器组实现结构

分析滤波器组的作用是对信号进行信道化处理，根据文献[9]可知，加权叠加结构分析滤波器组的实现结构如图2所示。

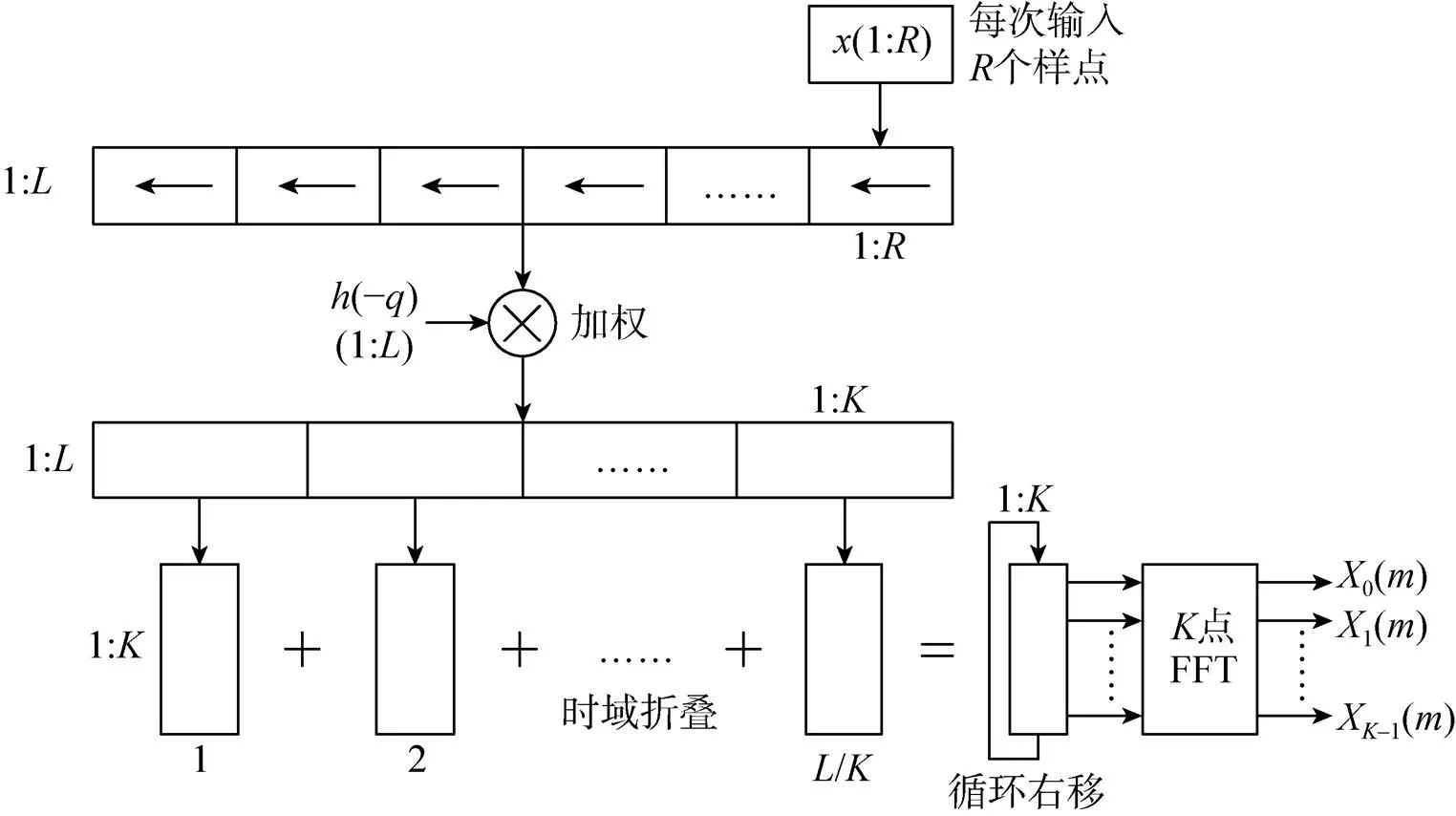
图2 WOLA分析滤波器组实现结构

其中，表示抽取倍数，表示信道数，表示原型滤波器长度。可以看出WOLA分析滤波器组的工作过程主要为数据分组、数据加权、叠接累加、循环移位和FFT运算，最终将输入信号划分为多个信道，完成信道化处理。

2.2 加权叠加结构综合滤波器组实现结构

经过信道化后的各个信道可以通过综合滤波器组进行合成，完成信号重构。下面对WOLA结构综合滤波器组的工作过程进行分析。图1中的信号重构过程可以用公式表示为

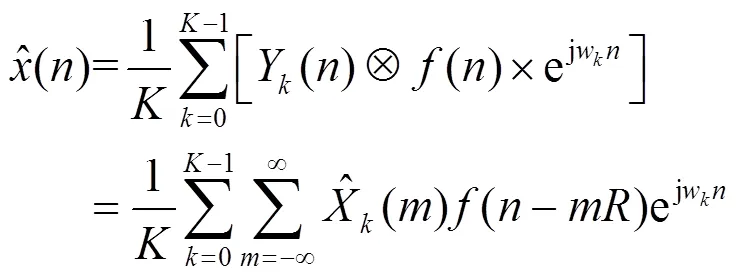
式中，

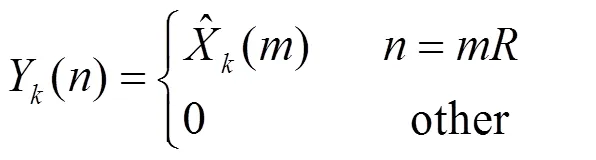
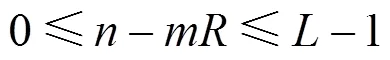
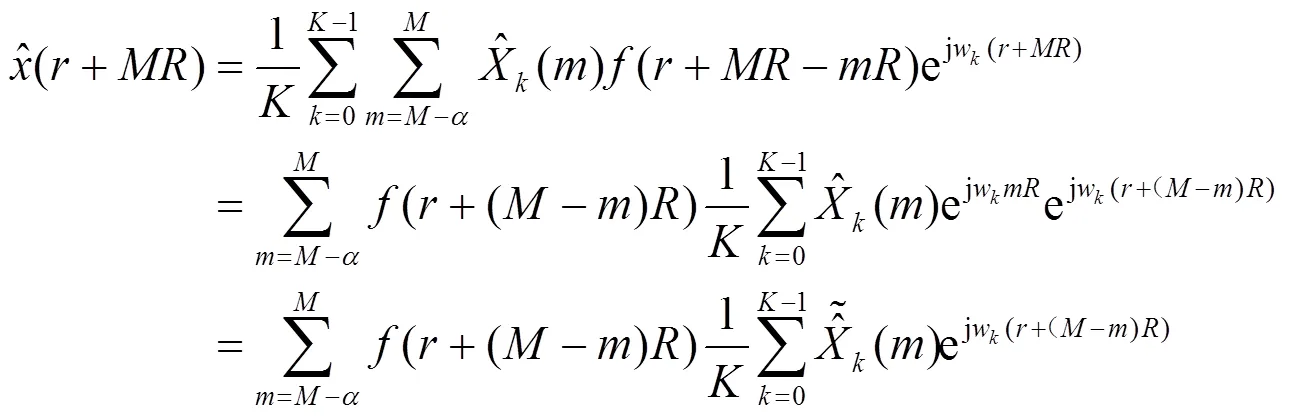
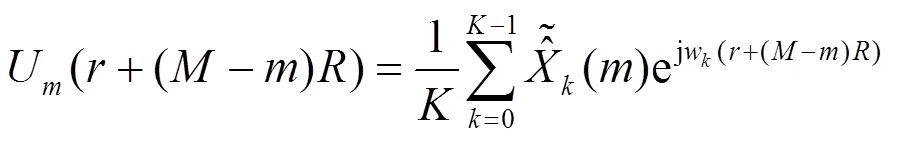
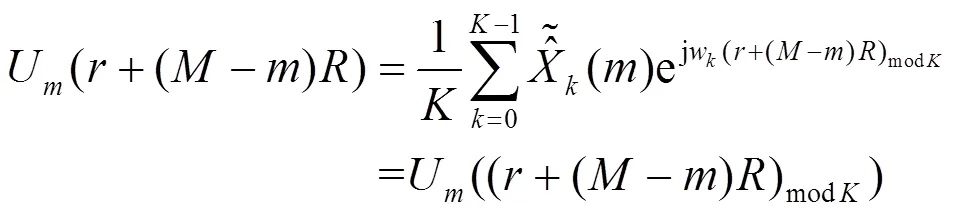
将式（5）代入式（3）中可得

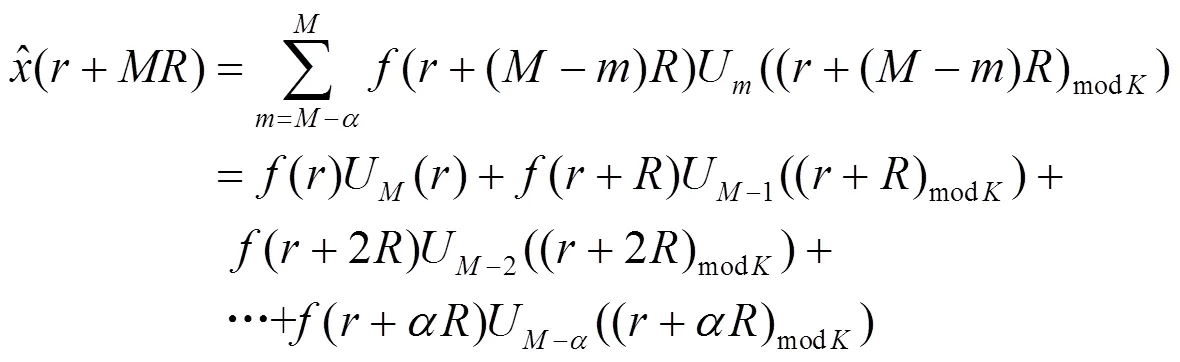
根据上述推导过程可得到WOLA综合滤波器组的实现结构，如图3所示。

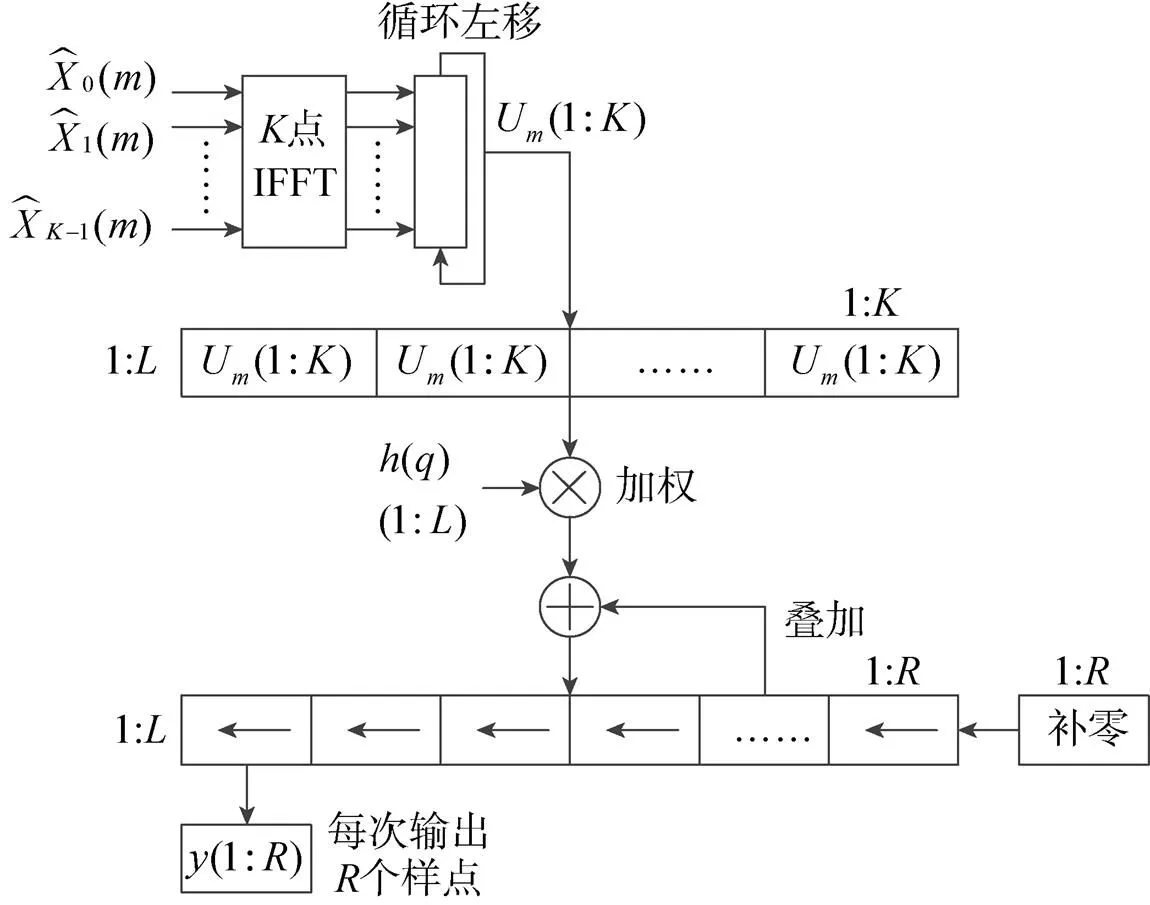
图3 WOLA综合滤波器组实现结构

根据上述结构图可以总结出WOLA综合滤波器组的工作过程，具体步骤如下：

①IFFT运算。对综合滤波器组的输入进行点IFFT运算。

③数据加权。首先将循环左移输出的个样点复制/份，将其存入初始状态为零、长度为的移位寄存器中，然后将移位寄存器中的个数据与滤波器()点对点相乘。

④叠接相加。构建一个长度为、初始状态为零的移位寄存器。在每个时刻将经过数据加权后的点数据与移位寄存器中的点数据点对点相加，然后从移位寄存器的一端输入长度为的全零数据，与此同时从另一端输出个数据，所有时刻输出的采样点连接在一起即为重构信号。

根据以上分析可知，WOLA结构滤波器组解除了系统信道数与抽取倍数的比值，即过采样因子必须为整数的限制，使得参数设置更加灵活。同时利用滤波器系数的加权运算替代了卷积运算，提高了运算效率。

3 加权叠加结构滤波器组动态信道化设计

由上节分析可知，WOLA结构滤波器组解除了系统过采样因子必须为整数的限制，是灵活高效的滤波器组。本节将WOLA结构滤波器组应用到动态信道化技术中，设计了一种基于WOLA结构滤波器组的动态信道化结构，如图4所示。

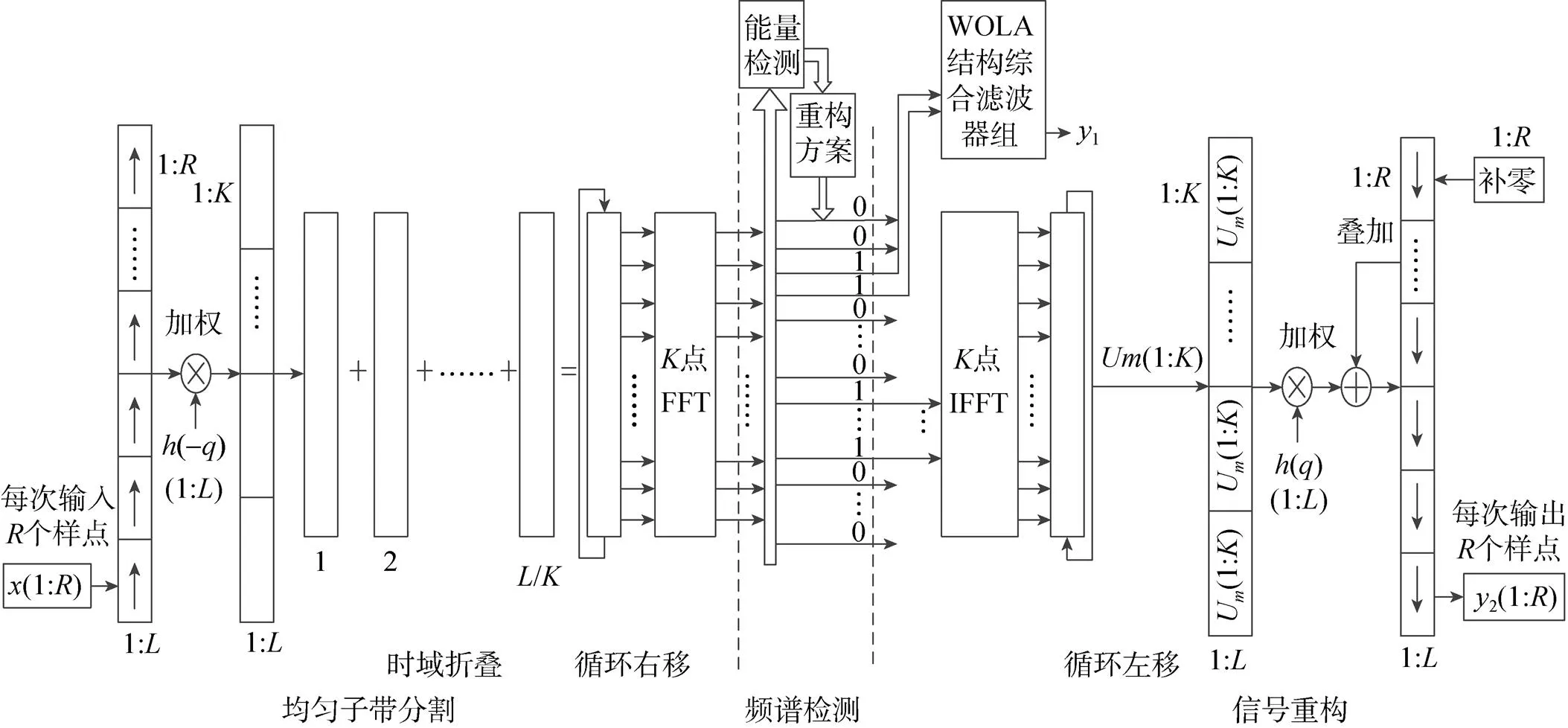
图4 加权叠加结构滤波器组动态信道化结构

为了简化，图中只画出了一组WOLA结构综合滤波器组的结构图，另外的利用简略图代替。

接收机接收到信号后送入WOLA分析滤波器组，通过分析滤波器组将接收带宽分割成若干个子信道，接收带宽内包含的信号也随之分散于各个信道。然后利用能量检测法对各个信道进行能量检测，存在信号的信道标记为“1”，不存在信号的信道标记为“0”。根据能量检测的结果，配置综合滤波器组的输入，当要提取某个信号时，该信号所在信道的数据保持不变，输入到综合滤波器组对应的信道，其他信道的输入全部置零，完成信号重构。当接收带宽内信号发生动态变化时，根据能量检测的结果动态配置综合滤波器组的输入，从而实现信号的动态提取。

与传统的DFT多相结构滤波器组动态信道化结构相比，本文提出的结构解除了过采样因子必须为整数的限制，提高了系统参数设置的灵活性。同时WOLA结构滤波器组利用滤波器系数的加权运算替代了原有的卷积运算，提高了运算效率。

4 仿真验证

本节将利用测试信号对WOLA结构滤波器组动态信道化结构进行仿真验证。采用单参数优化法设计具有重构特性的原型低通滤波器[10]，系统参数设置如表1所示。

表1 系统参数设置

4.1 有效性验证

初始状态接收带宽内包含了3个信号，信号的类型以及参数设置如表2所示。

状态一输入信号的时域波形和频谱图如图5所示。

表2 状态一信号参数

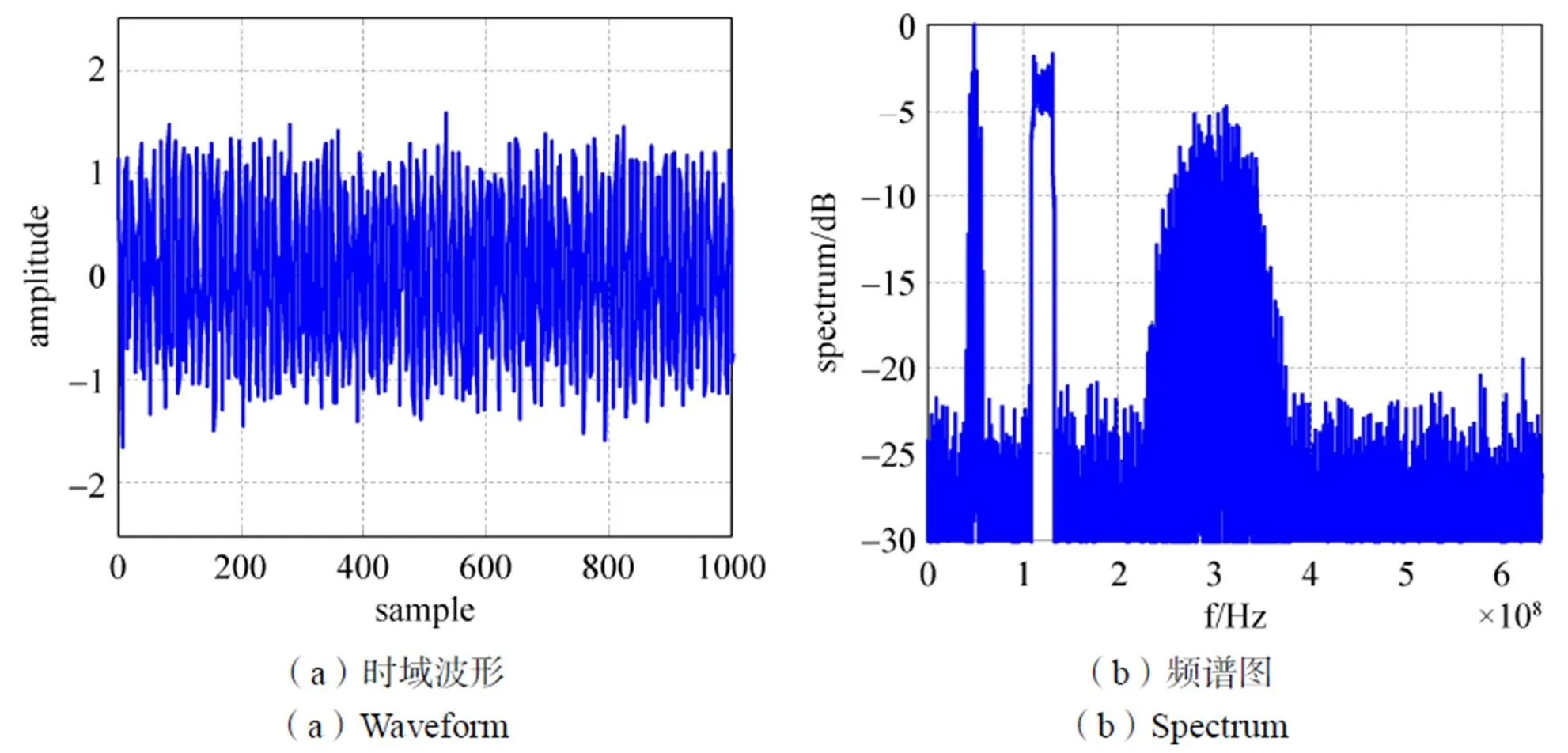
图5 状态一输入信号

由系统参数设置可知，状态一的输入信号被分析滤波器组划分成了256个信道，信道编号为0~255。然后再利用单门限能量检测法[11]对各个信道进行能量检测，检测结果说明了第8信道到12信道、第22信道到26信道、第44信道到76信道存在信号，与输入信号参数相符。将存在信号的信道送入综合滤波器组进行重构，结果如图6所示。

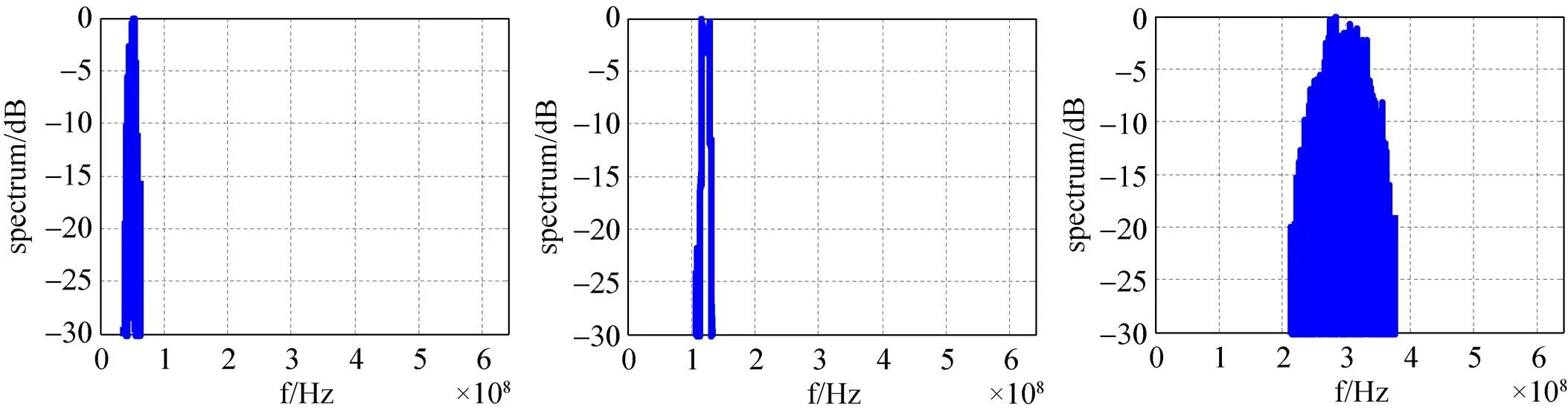
图6 状态一动态信道化结果

随后接收带宽内的信号分布发生动态变化，此时接收带宽内信号的参数如表3所示。

表3 状态二信号参数

状态二中接收带宽内信号的时域波形和频谱图如图7所示。

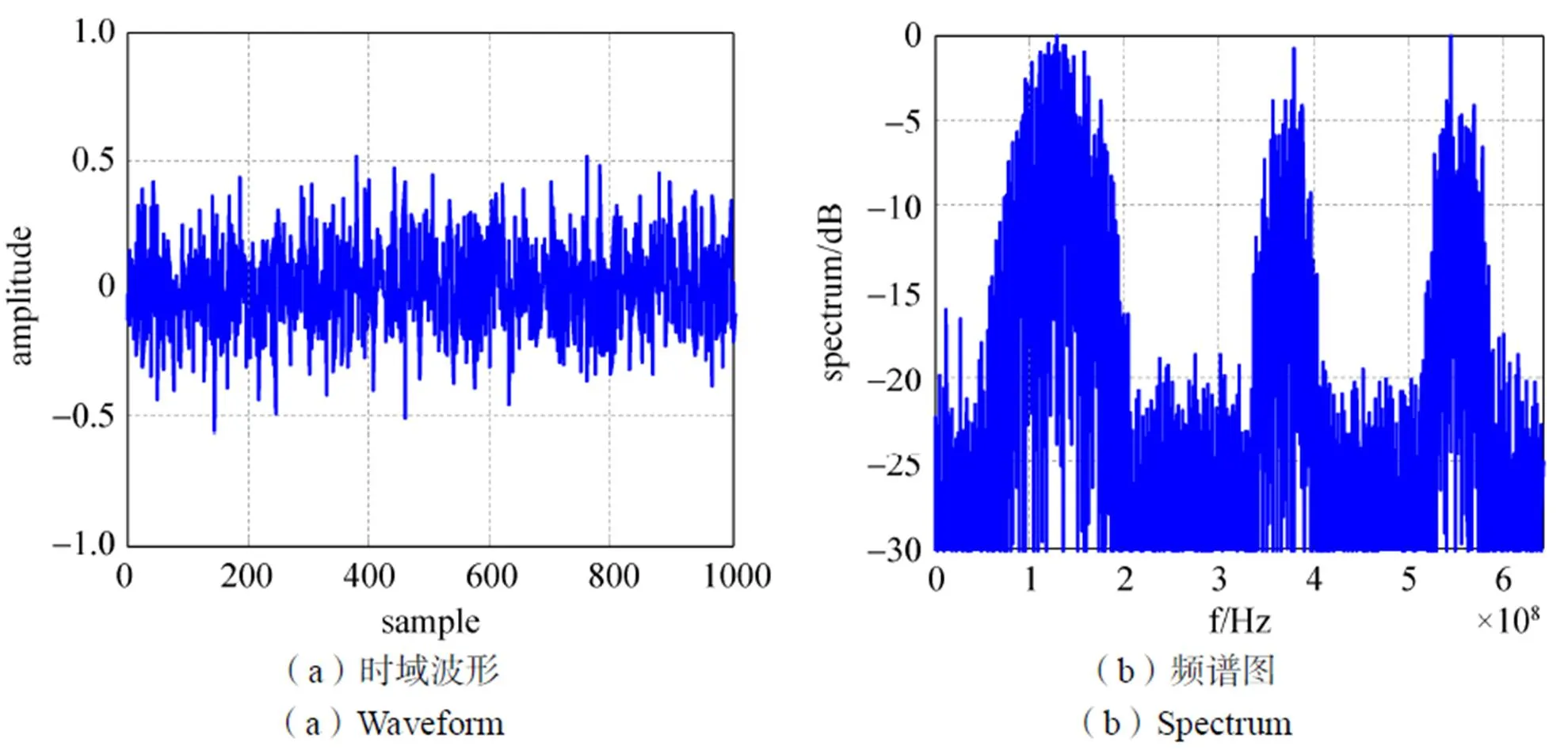
图7 状态二输入信号

与状态一相同，利用分析滤波器组将其划分为256个信道，利用单门限能量检测法测得包含信号的信道分别为第10信道到42信道、第66信道到82信道、第102信道到118信道，根据该结果配置综合滤波器组输入，完成信号重构，结果如图8所示。

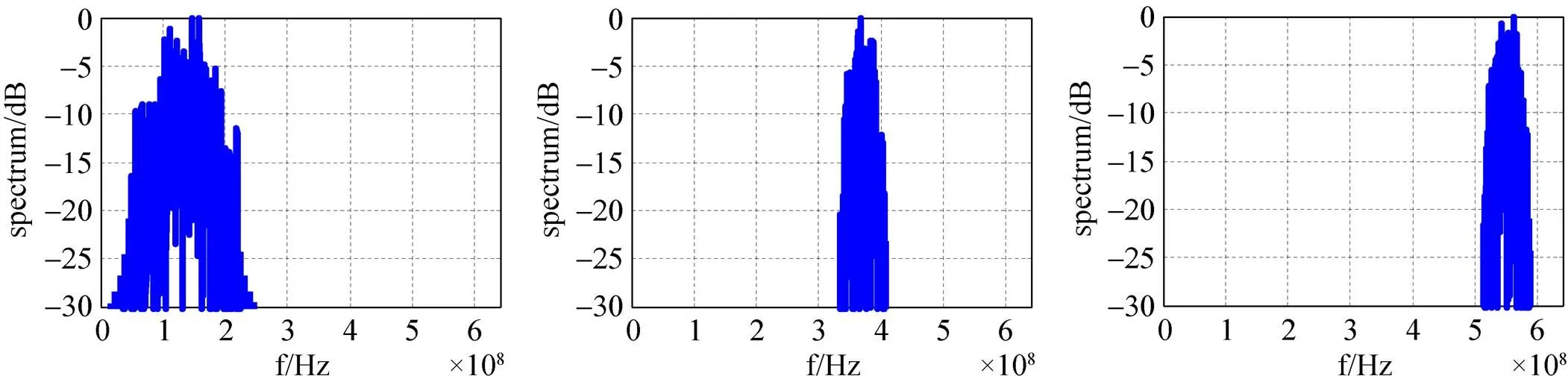
图8 状态二动态信道化结果

由此可以看出，基于WOLA结构滤波器组的动态信道化结构能够动态提取出接收带宽内包含的信号，验证了该结构的有效性。

4.2 两种结构重构误差比较

利用基于DFT多相结构滤波器组的动态信道化结构对状态一和状态二的信号进行提取，系统参数设置为信道数=256，抽取倍数=128，过采样因子=2。将两种结构所提取的重构信号与原信号的时域波形相减所得到的重构误差进行比较，结果如图9所示。可以看出，本文提出的基于WOLA结构滤波器组的动态信道化结构的重构误差比基于DFT多相结构滤波器组的动态信道化结构降低了一个量级，具有良好的重构特性。

5 结束语

本文提出了一种基于加权叠加结构滤波器组的动态信道化结构，将加权叠加结构滤波器组引入动态信道化技术中，解除了系统过采样因子必须为整数的限制。理论分析和仿真验证表明，WOLA结构滤波器组动态信道化结构能够动态提取接收带宽内存在的信号，且系统重构误差与传统DFT多相结构滤波器组动态信道化结构相比降低了一个量级，具有良好的重构特性。

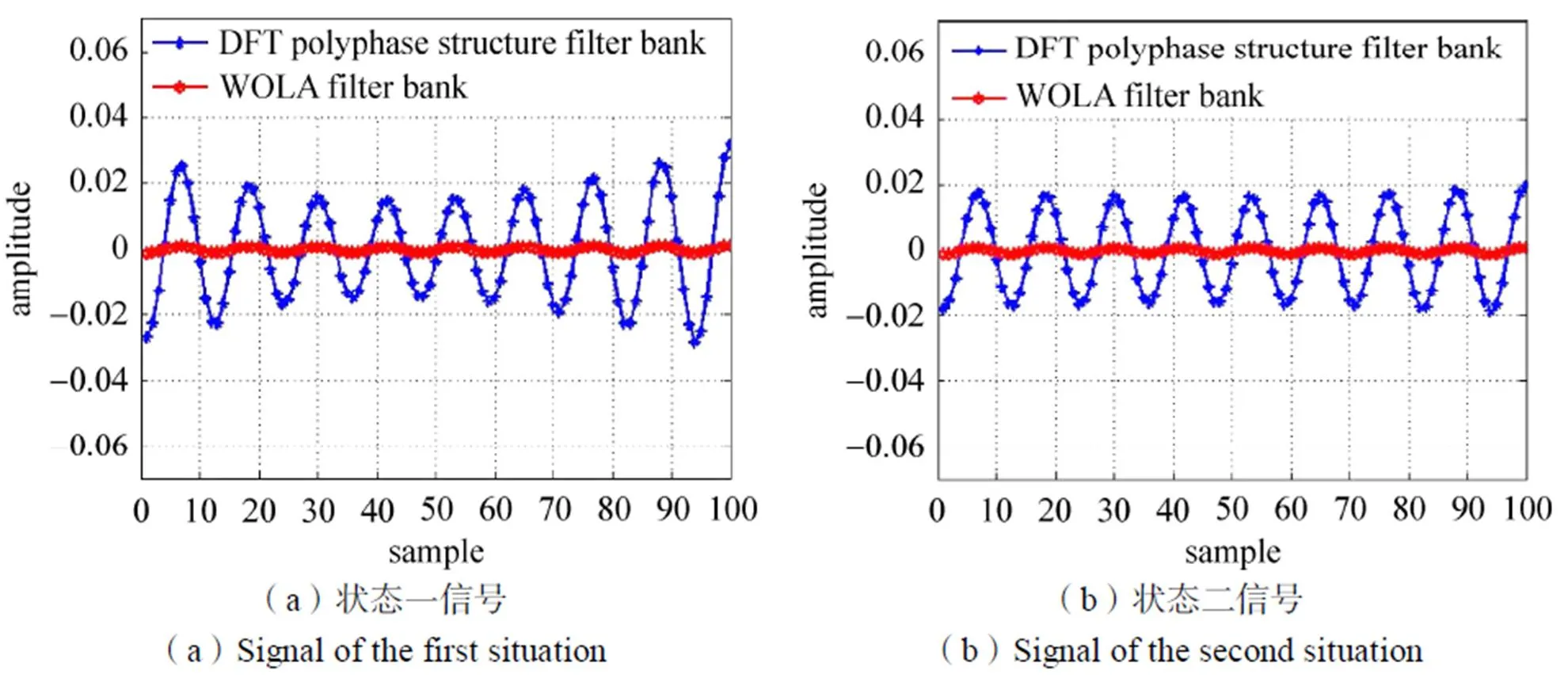
图9 重构误差比较

[1] 李程. 雷达电子侦察的多层次处理关键技术研究[D]. 长沙: 国防科技大学, 2015. LI Cheng. Research on key technologies in multi-level processing for electronic reconnais-sance of radar[D]. Changsha: National University of Defense Technology, 2015.

[2] DABCEVIC K, MUGHAL M O, MARCENARO L, et al. Cognitive radio as the facilitator for advanced communications electronic warfare solutions[J]. Journal of Signal Processing Systems, 2016, 83(1): 29–44.

[3] 李冰. 软件无线电中的信道化技术研究[D]. 郑州: 解放军信息工程大学, 2007. LI Bing. Research on channelization techniques for software defined radio[D]. Zhengzhou: PLA Information Engineering University, 2007.

[4] 李冰, 郑瑾, 葛临东. 基于非均匀滤波器组的动态信道化滤波[J]. 电子与信息学报, 2007, 29(10): 2396–2400. LI Bing, ZHENG Jin, GE Lindong. Dynamic channelization based on nonuniform filter banks[J]. Journal of Electronics and Information Technology, 2007, 29(10): 2396–2400.

[5] 胡君朋. 宽带无线信号侦测中的动态信道化技术研究[D]. 长沙: 国防科技大学, 2016. HU Junpeng. Research on dynamic channelization technique for broadband wireless signal reconnaissance[D]. Changsha: National University of Defense Technology, 2016

[6] NAVARRO R. Frequency domain beamforming for a deep space network downlink array[C]//IEEE Aerospace Conference, 2012: 1–8.

[7] CHEN X, HARRIS F J, VENOSA E, et al. Non-maximally decimated analysis/synthesis filter banks: applications in wideband digital filtering[J]. IEEE Transactions on Signal Processing, 2014, 62(4): 852–867.

[8] 王光宇. 多速率数字信号处理和滤波器组理论[M]. 北京: 科学出版社, 2013.

[9] 张超, 马宏, 焦义文. 一种改进的WOLA结构滤波器组在信道化中的应用[J]. 遥测遥控, 2018, 39(4): 44–49. ZHANG Chao, MA Hong, JIAO Yiwen. An improved WOLA filter bank for channelization[J]. Journal of Telemetry, Tracking and Command, 2018, 39(4): 44–49.

[10] DOBLINGER G. A fast design method for perfect-reconstruction uniform cosine-modulated filter banks[J]. IEEE Transactions on Signal Processing, 2012, 60(12): 6693–6697.

[11] JOSHI D R, POPESCU D C, DOBRE O A. Adaptive spectrum sensing with noise variance estimation for dynamic cognitive radio systems[C]//44th Annual Conference on Information Sciences and Systems, 2010: 1–5.

Research on dynamic channelization structure based on WOLA filter bank

MA Hong, ZHANG Chao, JIAO Yiwen

（Space Engineering University of PLA, Beijing 101416, China）

Aiming at the problem that the dynamic channelization structure based on traditional DFT polyphase structure filter bank requires an integer oversampling factor, which limits the flexibility of parameter setting, a flexible and efficient Weighted Overlap-add (WOLA) filter bank is introduced into the dynamic channelization structure. The implementation structure of WOLA integrated filter bank is obtained through the formula deduction, and the dynamic channelization structure based on WOLA filter bank is designed.The simulation results show that the designed dynamic channelization structure releases the limitation of integer oversampling factor, which enhances the flexibility of parameter setting. Compared with the dynamic channelization structure based on DFT polyphase structure filter bank, the reconstruction error of the dynamic channelization structure based on WOLA filter bank decreases by an order of magnitude.

Dynamic channelization; WOLA structure;Flexibility;Reconstruction error

TN927

A

CN11-1780(2019)02-0069-08

基金项目：国家自然科学基金资助项目（91738201）

2018-12-25

2019-02-21

马 宏 1976年生，工学博士，副教授，硕士研究生导师，研究方向为高速数字信号处理。

张 超 1993年生，硕士研究生，研究方向为飞行器测控技术。

焦义文 1985年生，工学博士，讲师，研究方向为航天测控。