基于渗流作用被锚巷道弹塑性分析

樊 琪，李红霞，李晓栋

(1.中煤科工集团 西安研究院有限公司，陕西 西安 710077；2.西安科技大学 管理学院，陕西 西安 710054；3.西安科技大学 建筑与土木工程学院，陕西 西安 710054)

0 引 言

随着我国煤炭产量和开采强度的不断增大，开采逐渐向地质和应力条件复杂的环境中进行。地下水是岩体赋存的环境因素之一，渗流对岩体的变形和稳定产生了严重的影响。因此考虑渗流作用下对巷道围岩进行弹塑性分析一直是一个热点问题[1]。

不考虑渗流时，国内外学者对巷道围岩应力与位移的分布做了大量的研究。巷道围岩弹塑性解最先由Fenner提出[2]，紧接着学者提出来修正的Fenner公式以及Kastner公式得到广泛应用[3-4]；谷拴成等基于统一强度理论，推导了不同主应力条件下相对应的塑性区宽度计算公式[5]；方勇、文竞舟等分析了全长粘结锚杆与围岩之间的力学本质，求得隧洞围岩塑性区范围表达式[6-7]；Osgoui，Indraratna等根据锚杆密度因子对围岩的强化作用，推导出了锚杆支护下隧洞的解析解[8-9]；谷拴成等将锚杆与围岩考虑成均质的加固体，对该模型进行弹塑性分析[10-11]。

考虑渗流作用时，近年来国内外学者也有不少研究，SeokWon Lee，In-Mo Lee等推导了渗透力作用下洞室围岩特性曲线解析解[12-13]；孙珍平、李宗利、吕晓聪等研究了渗流作用下圆形隧洞弹塑性的解析解[14-16]；黄阜等考虑渗透力的作用，绘制了基于原始Hoek-Brown屈服准则的围岩特性曲线[17-18]；张丙强等将Izbash非Darcy渗流模型引入渗流理论，求解得到非线性渗流场[19]；荣传新等根据损伤理论，求得渗流作用下巷道损伤区半径方程。然而在考虑渗流作用时，将锚杆对围岩的支护作用与渗流作用同时考虑并进行围岩应力场和位移场的研究较少[20]。

综上，本文通过考虑渗流的影响，将锚杆的加固作用与地下水渗流的弱化作用同时等效为附加在围岩中的体积力，通过锚杆对围岩参数的强化，利用Mohr-Coulomb准则对巷道围岩进行弹塑性分析，推导了围岩弹塑性位移和应力的解析表达式，求得巷道围岩塑性区半径和洞壁位移的解析解。在此基础上分析不同锚杆支护参数对渗流作用下巷道围岩塑性区范围和洞壁位移的影响。

1 渗流场计算与力学模型

1.1 渗流场计算

岩体的渗流满足达西定律：假定材料渗透系数相同，渗流方向主要以径向为主，忽略浮力和水自重的影响[21]，R为渗流影响半径，pw(r)为孔隙水压。根据达西定律可知渗透微分方程为

(1)

边界条件为

pw|r=R0=0,pw|r=R=pm

(2)

式中pm为渗流影响半径R处孔隙水压力，MPa；R0为巷道半径，m.

通过式(1)和式(2)可得孔隙水压力分布形式为

(3)

则围岩中的渗流体积力可以表示为

(4)

1.2 建立力学模型

考虑渗流作用锚杆支护下的围岩变形应作如下假定

1)巷道为圆形；

2)将围岩视为均匀、连续的多孔介质，围岩性质为理想弹塑性体，处于平面应变状态；

3)锚杆处于弹性状态，锚杆存在于围岩塑性区中；

4)原岩应力为各向等压状态。

在外压作用下，锚杆与围岩相互作用，在锚固体内，将锚杆对围岩的支护反力转化为锚固区围岩附加体积力f(r).围岩强度参数为c和φ，锚固后的围岩强度参数为cs和φs，锚杆长度为L，围岩塑性区半径为Rp，锚固体半径为R1(R1=R0+L)，原岩压力为p0，力学模型如图1所示。

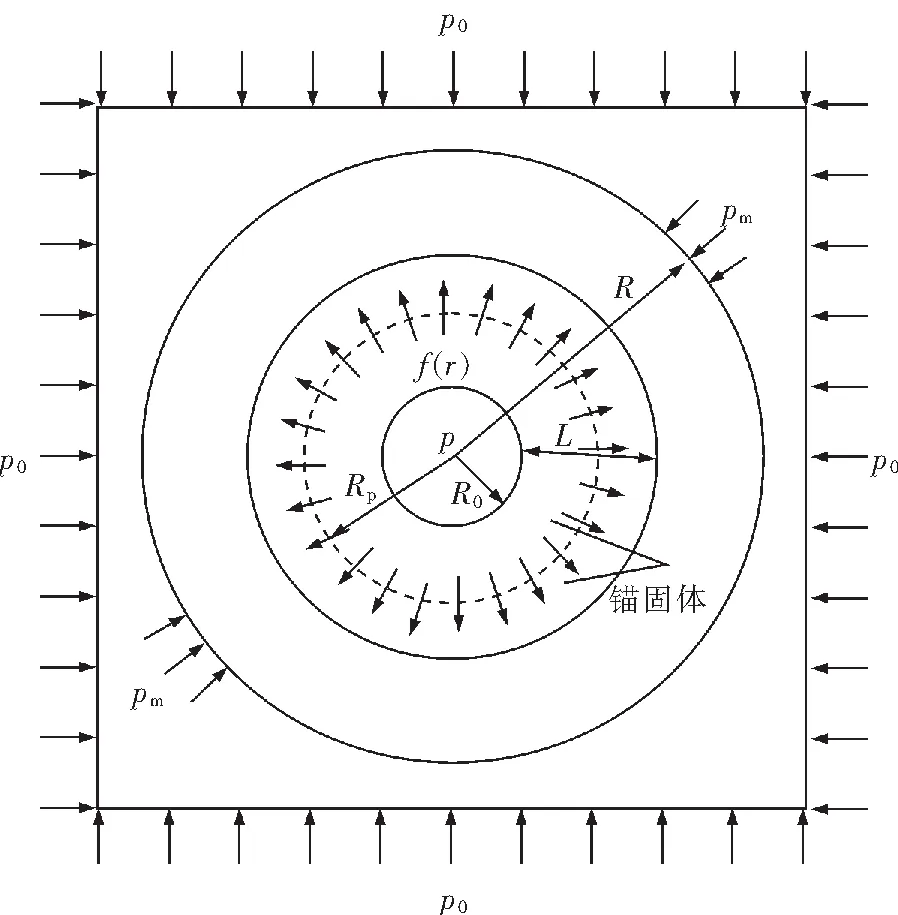
图1 力学模型Fig.1 Mechanical model

2 确定力学参数

2.1 锚固体附加体积力f(r)

取锚杆微段dr进行分析，如图2所示。

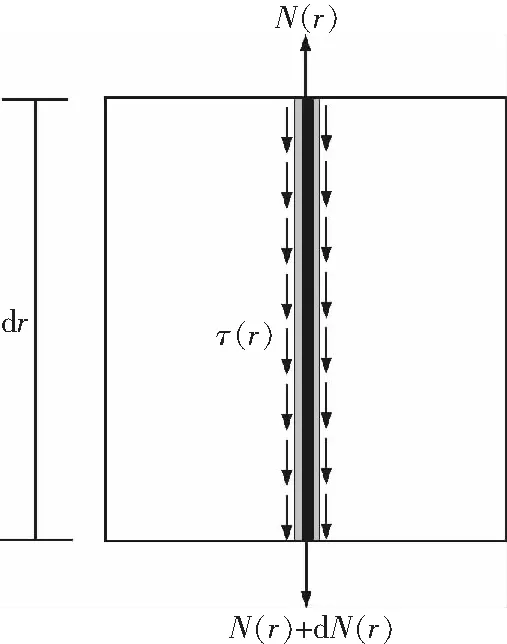
图2 锚杆微元体Fig.2 Bolt micro-body

由中性点理论可知，中性点处锚杆界面剪应力为0，故可以用中性点处的围岩位移表示锚杆的整体位移[22]，锚杆界面剪应力为

(5)

式中Gm为锚固剂部分的剪切模量，GPa；tm为锚固剂厚度，mm；a为锚杆中性点至圆形巷道中心的距离，m.

对锚杆施加预紧力，整体分析可得

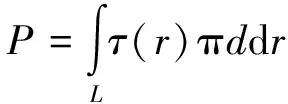
(6)

式中d为锚杆直径，mm；P为锚杆预紧力，kN；L为锚杆长度，m.

对锚杆微元体分析(图2)，列静力平衡方程可得锚杆轴力N(r)为

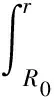
(7)

假设单根锚杆作用的影响范围为相邻两根锚杆距离的一半，单根锚杆与围岩耦合单元如图3所示，则围岩体积力f(r)分布为

(8)

式中Sr为周向间距，rad；SL为纵向间距，m.

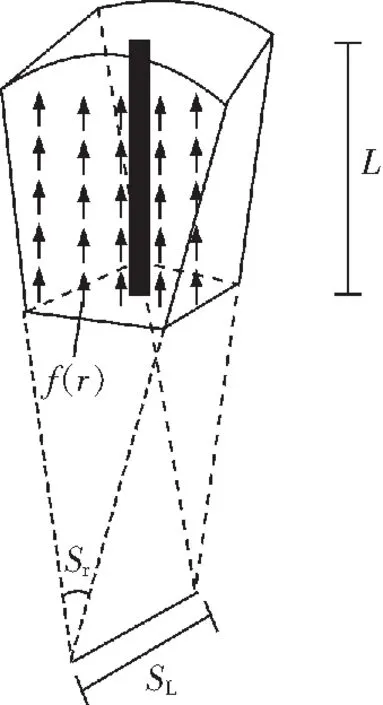
图3 单根锚杆与围岩协调变形单元Fig.3 Single bolt and surrounding rock coordination deformation unit

2.2 锚固体强度参数cs和φs

锚杆支护改善被锚围岩的应力状态，并使其强度指标得到了一定的提高，即黏聚力和内摩擦角。

研究表明，支护前后围岩的内摩擦角变化很小[23]，所以锚杆加固后锚固体的内摩擦角可表示为

φs=φ

(9)

式中，φ为岩体内摩擦角，(°)。

锚固体的最大主应力方向与锚杆垂直，则锚固体主破裂面方向与最大主应力方向的夹角α=π/4-φ/2[24]。

锚杆的横向作用提供的黏聚力为

(10)

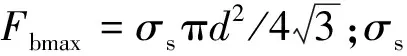
锚杆轴向作用提供的黏聚力为

(11)

由以上分析可知，锚固体的黏聚力为

(12)

3 弹塑性分析

3.1 塑性区应力分析

当考虑渗流时，锚固体塑性区应力分量应满足Mohr-Coulomb准则

(13)

由岩土弹塑性力学理论可知，围岩在受到锚杆支护和孔隙水压力时，平衡微分方程表示为

(14)

联立式(4)、(8)、(13)和(14)，并带入边界条件σrp(R0)=0，解得锚固体塑性区应力分布为

(15)

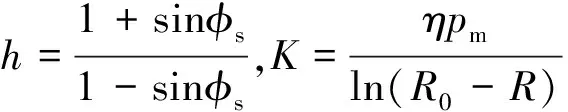
3.2 弹性区应力位移分析

通过平衡方程式(14)，几何方程，物理方程，解得弹性区应力和位移表达式为[25]

(16)

式中i=1为锚固体弹性区；i=2为围岩弹性区，并且

边界条件为

(17)

将边界条件代入式(16)，可解得C，D

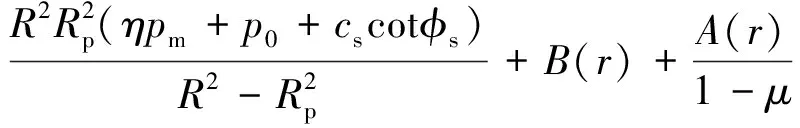
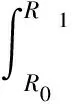
3.3 塑性区半径

(18)

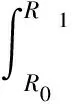
3.4 塑性区位移

假设塑性区体积不可压缩，形状可能发生改变，则塑性区位移为

(19)

由式(18)可解得洞壁位移为

(20)

4 算例分析

某圆形巷道的半径R0=3.5 m，渗流影响范围R=40 m，岩体的物理力学参数为：弹性模量E=2 100 MPa，泊松比μ=0.3，黏聚力c=0.8 MPa，内摩擦角φ=30°，原岩压力p0=10 MPa，孔隙水压力pm=2 MPa.锚杆物理力学参数为：锚固剂剪切模量Gm=5 GPa，锚固剂厚度tm=10 mm，锚杆周向间距Sr=2/7 rad，纵向间距SL=1.0 m，预紧力P=60 kN，直径d=22 mm，屈服强度为335 MPa或400 MPa.

为了验证本文计算模型的合理性，采用FLAC3D数值模拟方法进行对比分析。巷道开挖后围岩的应力与位移仅在洞室周围变化较大，因此模型选用50 m×50 m×50 m.锚杆采用线弹性材料，模型边界作用原岩压力p0和孔隙水压力pm，模型有10 200个单元组成，其中包含12 060个节点。

表1 理论与模拟结果对比

通过考虑渗流作用，采用本文理论与FLAC3D软件分别求得考虑渗流与不考虑渗流下被锚巷道围岩塑性区半径与洞壁位移(表1)，可以看出理论计算值与数值模拟结果相差小于10%，从而说明了该方法的准确性和合理性。

下面结合算例，分析巷道半径和锚杆支护强度对围岩塑性区半径和洞壁位移的影响。

4.1 巷道半径影响规律

如图4所示，可以看出未进行锚杆支护时，当巷道半径从0 m增加到8 m时，不考虑渗流作用下塑性区半径从0 m增加到16.235 m，考虑渗流作用(pm=2 MPa)下塑性区半径从5.15 m增加到32.03 m.当锚杆屈服强度从335 MPa变为400 MPa时，塑性区半径大约减小了5%，因此考虑渗流作用时对塑性区范围影响更严重。

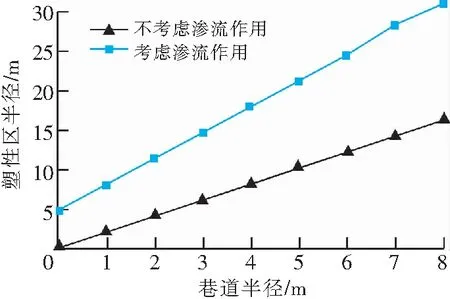
图4 巷道半径对塑性区半径的影响Fig.4 Influence of roadway radius on radius of plastic zone

4.2 锚杆长度影响规律

图5 锚杆长度对塑性区半径的影响Fig.5 Influence of bolt length on radius of plastic zone

图6 锚杆长度对洞壁位移的影响Fig.6 Influence of bolt length on displacement of cave wall

锚杆长度的影响如图5和图6所示，可以看出，塑性区半径和洞壁位移在不考虑渗流与考虑渗流(pm=1 MPa和pm=2 MPa)工况下随着锚杆长度的增加而减小，但随着锚杆长度增大，增幅在减小。当锚杆长度从1.5 m增加到4.2 m时，考虑渗流作用与不考虑渗流作用下塑性区半径大约减小了13%，12%和8%，洞壁位移大约减小了12%，12%和10%.在锚杆长度改变的条件下，锚杆屈服强度从335 MPa变为400 MPa时，3种工况下塑性区半径和洞壁位移分别大约减小了4.3%和4.8%.

4.3 锚杆排距影响规律

锚杆排距的影响如图7和图8所示，可以看出，塑性区半径和洞壁位移在不考虑渗流与考虑渗流(pm=1 MPa和pm=2 MPa)工况下随着锚杆排距的增加而增大，但随着锚杆排距增大，增幅在减小。当锚杆排距从0.8 m增加到1.8 m时，考虑渗流作用与不考虑渗流作用下塑性区半径大约增加了14%，13%和10%，洞壁位移大约增加了14%，14%和8%.在锚杆排距改变的条件下，锚杆屈服强度从335 MPa变为400 MPa时，3种工况下塑性区半径和洞壁位移分别大约减小了4.5%和5%.

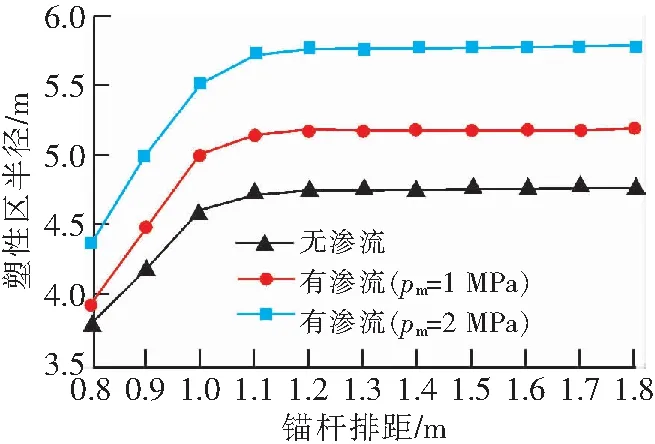
图7 锚杆排距对塑性区半径的影响Fig.7 Influence of bolt spacing on the radius of plastic zone

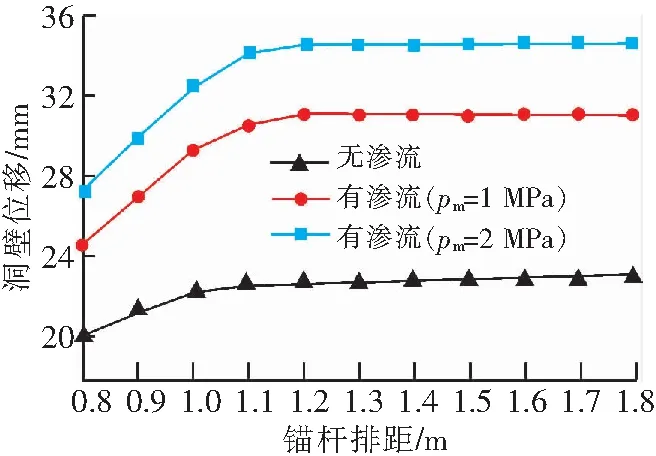
图8 锚杆排距对洞壁位移的影响Fig.8 Influence of bolt row spacing on displacement of cave wall

4.4 锚杆预紧力影响规律

锚杆预紧力的影响如图9和图10所示，可以看出，塑性区半径和洞壁位移在不考虑渗流与考虑渗流(pm=1 MPa和pm=2 MPa)工况下随着锚杆预紧力的增加而减小。当锚杆预紧力从0 kN增加到200 kN时，考虑渗流作用与不考虑渗流作用下塑性区半径大约减小了32%，32%和26%，洞壁位移大约减小了36%，35%和27%.在锚杆预紧力改变的条件下，锚杆屈服强度从335 MPa变为400 MPa时，3种工况下塑性区半径和洞壁位移分别大约减小了4.6%和5.2%.

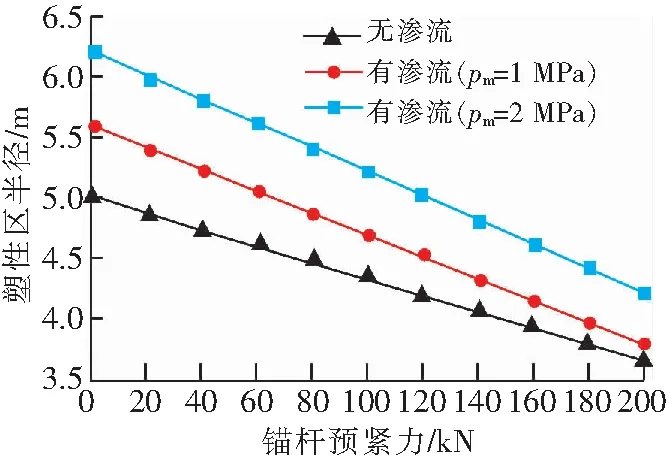
图9 锚杆预紧力对塑性区半径的影响Fig.9 Influence of bolt preload on radius of plastic zone

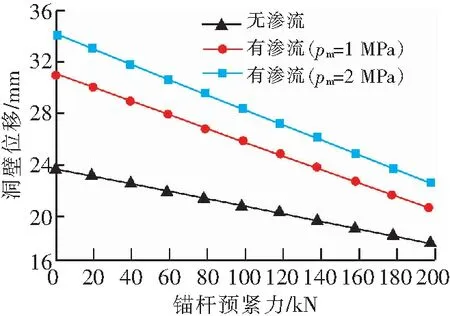
图10 锚杆预紧力对塑性区半径的影响Fig.10 Influence of bolt preload on radius of plastic zone

5 结 论

1)将锚杆支护与围岩协调变形效果等效为锚固体上的支护体积力，提高锚固体强度参数c，φ值，并考虑渗流作用，将渗流力转化为体积力，建立了考虑渗流作用下锚杆支护巷道围岩力学计算模型。

2)在考虑渗流作用的基础上，运用M-C准则，推导出了在渗流作用下锚杆支护的巷道围岩的应力与位移分布，求出了渗流作用中锚杆支护下巷道洞壁位移与塑性区半径。

3)根据算例，通过对渗流作用下和无渗流作用下巷道塑性区范围和洞壁位移影响因素进行分析，得出巷道半径、锚杆长度、锚杆排距以及锚杆预紧力对巷道塑性区半径和洞壁位移的影响，因此在巷道支护设计中应充分考虑地下水引起的渗流作用。

4)锚杆长度和预紧力与塑性区范围和洞壁位移成反相关关系，锚杆排距与塑性区范围和洞壁位移成正相关关系。因此锚杆支护参数对支护效果更敏感。在相同的条件下，锚杆长度越大，排距越小，预紧力越大，巷道围岩越稳定。