随机森林和水平集的椎骨CT分割方法
陶永鹏,景 雨,顼 聪
(大连外国语大学 软件学院,辽宁 大连 116044)
1 概 述
脊柱,是人体中央负重骨骼,是人体上半身结构的中轴线.新型扫描技术中CT是评估三维空间椎骨形态最精确的方式.椎骨CT图像分割是诊断的基本步骤和任务,如识别脊椎异常诊断[1],生物力学建模或图像引导脊柱干预[2].为了保证分割的准确性,图像引导脊柱干预等通常需要亚毫米级精度.但由于椎骨形状的复杂性和结构的变化性等特点,传统的图像分割方法并不适用于椎骨的分割.
近年来,众多学者已提出部分针对椎骨图像的分割算法.一些无监督的图像处理方法也被应用于椎骨的分割,流域[3]和图形[4]等处理复杂拓扑结构的水平集方法被应用于椎骨分割.Lim等[5]将Willmore流程纳入水平集框架来拟合表面模型的演变.黄等[6]结合边缘和基于区域的水平集函数实现CT图像中椎体的分割.李等[7]提出了一种自动初始化水平集方法,实现基于混合形态滤波和高斯混合模型处理拓扑变化.Klinder等[8]提出了集成检测框架,基于脊柱曲线提取和统计形状模型识别和分割椎骨.Roberts等[9]使用主动形状模型将椎骨分成几部分进行分割协作,可应用于二维射线图像并可以扩展到三维.唐利明[10]等提出了变分水平集的分割模型提高了对噪声图像的分割能力,但受聚类数目的影响较大.这些模型在某种程度上达到了较高的分割准确度,但初始姿态较敏感,部分并且需要对图像手动改动.
目前,机器学习技术已被应用于医学CT图像.简[11]等使用随机森林分类算法成功的从存在背景干扰和光照变化的图像中实现了目标检测,但该方法并不能确定器官的范围.Pauly等[12]应用随机蕨类(random ferns),同时引入 3DLBP(Local Binary Patterns)特征,实现了对 MR 图像中多重解剖结构位置和大小估计.Glocker[13]采用一种有向距离图谱对人体器官进行检测,将有向距离图谱作为目标边界形状的隐式表达,通过边界内外体素的正负值进行检测.
2 本文方法
本文针对椎骨图像分割中对初始轮廓敏感的问题,提出基于加权随机森林和水平集分割的椎骨CT分割方法.提取CT图像的SIFT特征,通过随机森林分类回归算法选择距离图谱中距离值最小的100个点进行Mean-shift 聚类分析,产生聚类中心,重建操作后获得对应的3D距离预测图谱,选取距离最小的点作为随机森林确定的椎骨中心点.随后将获得的椎骨中心点作为CV分割模型的初始轮廓位置,通过求解平稳控制演化速度和噪声敏感度的CV模型,由能量函数演化方程最小值来实现对椎骨CT图像的分割.方法示意图如图1所示.
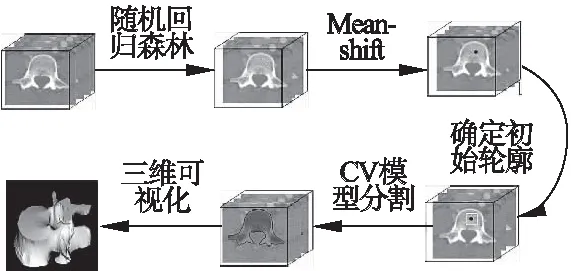
图1 方法示意图Fig.1 Schematic of the method
3 SIFT特征
SIFT特征(Scale-invariant feature transform)是一种图像局部特征提取算法,能够保持较好的稳定性.在描述子的生成过程中,对于16×16的关键点邻域,在处理梯度时进行高斯加权处理,强化中心区域,淡化边缘区域的影响.在每个4×4 子区域上计算8个方向的梯度方向直方图,即形成一个种子点,每个关键点描述子由4×4=16个种子点组成,每个种子点有8个梯度方向信息,形成4×4×8=128维的SIFT特征向量.
4 随机森林
本文方法将训练数据点定义为Dk=(Sk,Ck),其中Sk是基于体素k得到的SIFT特征向量,Ck是体素k到标记椎骨中心点i的距离.概率密度函数为p(Ck|Sk).随机森林回归目标函数I(Dj,θ)定义为:
(1)
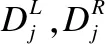
本文采用连续形式的微分熵:
(2)
样本数据点D,采用连续高斯模型密度分布p(Ck),并将b元高斯的微分熵函数定义为:
(3)
根据一维输入与输出的回增益表达式推导过程[14],推广到多元变量的情况可得:
(4)
其中,Λy为条件协方差矩阵,可以得到一棵决策树的后验概率pt(Ck|Sk),对T棵树的后验概率求平均值,T为决策树数量,并将后验概率平均值作为回归的结果.
(5)
因为决策树之间的决策结果差异较大,随机森林中决策树的性能越好的决策树应该占有更高的比重.为解决这个问题,对随机森林中的决策树采取加权运算,来提高准确率.每棵决策树的可信度可由公式(5)计算得到的后验概率表示.
随机森林初始化时,所有树的权值相同,为:
ω0(k)=1/T
(6)
本文提出随机回归森权重公式为:
(7)
其中,ω(k)表示分类森林中第k棵决策树的权重,γ(k)为第k棵决策树的回归中心与专家标记点间的距离,γ(k)越大所占权重越小,通过迭代优化最小绝对误差函数来训练随机回归森林.
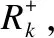
4.1 水平集演化分割
由于水平集分割模型对初始轮廓敏感且脊柱CT图像的灰度不均匀分布,可能会导致陷入局部最小,分割不完全.为了减小误差,将初始轮廓置于随机森林定位的椎骨中心点上并设定曲线由内向外演化.
令I为区域Ω上的一幅椎骨CT图像,将分割的初始轮廓L选取在随机森林算法确定的椎骨中心点位置,并使用水平集分割算法对椎骨CT进行分割,设定轮廓由内向外膨胀.
将边缘指示函数定义为:
(8)
其中Gσ是标准方差为σ的高斯核函数,像素为D(x,y).引用两个参数来调整水平集演化的速度及噪声敏感度,β>0,γ>0,其中β用来调整演化速度,γ用来控制噪声敏感度.
引进参数后,将新的水平集能量方程定义如公式(9).
E(φ)=αRp(φ)+λLl(φ)+ηAl(φ)
(9)
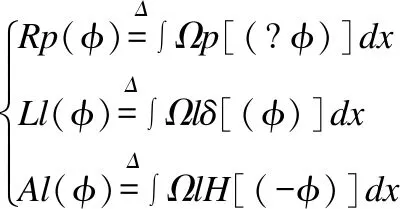
(10)
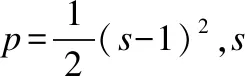
使用梯度下降法将公式(7)的能量方程进行最小化求解得到水平集演化方程如公式(11):
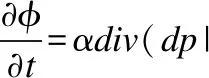
(11)
通过逆向有限差分算法,可得:
(12)
根据公式(10)进行水平集函数φ的演化,直至演化曲线达到稳定状态后停止演化.为使分割更为准确,对达到稳定状态的停止演化的曲线进行平滑曲线操作,作为最终的分割输出结果,完成椎骨CT图像分割.
本文方法实现椎骨CT图像分割步骤如图2所示.
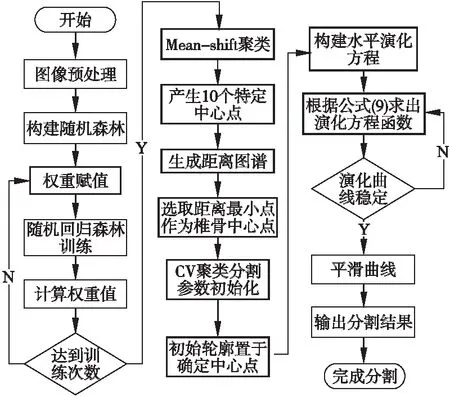
图2 分割步骤Fig.2 Segmentation step
4.2 分割结果
本文使用公开的椎骨CT分割挑战数据集,对数据集中提供的20组脊柱CT图像共计1190张CT图像进行分割实验.实验环境为Intel Pentium 3.2 GHz CPU、4GHz GPU、MATLAB R2010a.实验结果如图3所示.
在图3 (a)为初始轮廓椎骨CT的分割结果;图3(b)为椎骨中心点位置,其中黑色点为最终确定椎骨中心点,周围浅色区域为待定中心点;图3(c)轮廓分割初始轮廓选取结果,其中白色方框为初始轮廓;图3(d)本文方法椎骨分割结果,深色区域为本文方法分割结果,白色区域为专家手动分割真实值;图3(e)为整个胸椎和腰椎的分割结果图.
本文方法对椎骨可以准确、稳定地分割,相比其他算法对于任意位置初始轮廓的分割结果,准确性具有很大的提高.为了能够更直观的观察椎体的分割效果,对腰椎椎骨L3、L4、L5的分割结果进行了三维重建,如图4所示.
根据骰子系数(DC),对本文方法进行评估和对比,其定义如下:
(13)
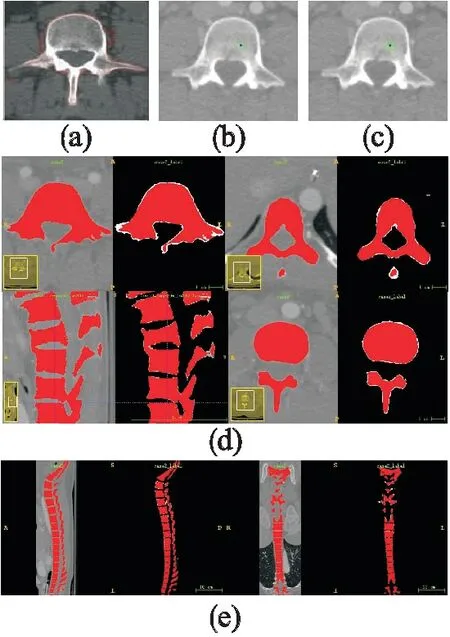
图3 椎骨切片分割结果Fig.3 Vertebral slice segmentation result
其中,Sr是参考体积,Ss是分割体积.将脊柱分为三段(T1-T6,T7-T12和L1-L5)对分割的平均骰子系数进行计算,本文方法分割结果骰子系数平均为0.936,具体结果如表1所示,随机抽取4组脊柱CT进行了分割结果的骰子系数统计,结果如图5所示.
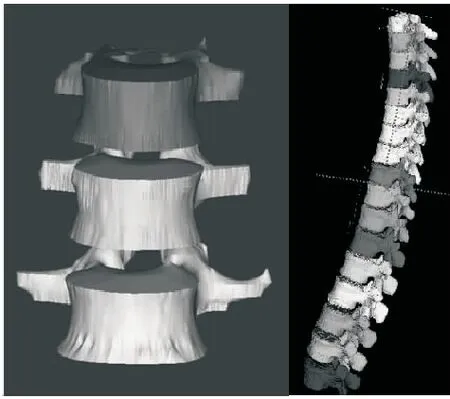
图4 腰椎分割结果三维可视化Fig.4 3D visualization results of lumbar segmentation

T1-T6T7-T12L1-L5All骰子系数0.9250.9320.9510.936
表2对本文方法的椎骨分割结果与其他3个算法进行了详细比较.方法1只分割了腰椎区域,不能分割胸椎区域;方法1和方法2需要对椎骨进行手动定位;方法3和本文方法能够对椎骨自动定位,本文方法分割更准确.本文方法分割骰子系数平均为0.936,能够自动定位中心位置并有较高的分割准确率.
表2 椎骨CT分割结果对比
Table 2 Comparison of CT segmentation results of vertebrae

方法椎骨定位分割方法骰子系数DC方法1[15]手动定位统计形状模型0.930方法2[16]手动定位平均形状模型0.934方法3[17]自动定位平均形状模型0.930本文方法 自动定位WRF-CV 模型0.936
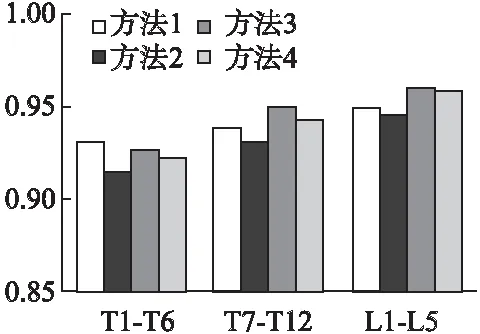
图5 测试CT集分割结果Fig.5 Test CT set segmentation results
5 结束语
本文提出了基于加权随机森林和CV模型的椎骨CT图像分割方法.通过对不同数据进行实验得出,本文提出的算法能够成功定位椎骨中心位置,能够有效解决因初始轮廓不正确而造成的过分割和分割不完全的问题,在自动定位和准确性方面具有一定的优势.在之后的研究学习中,还需要研究更为通用的椎骨CT图像分割方法,提高自适应性.

