一类严格反馈非线性时滞系统的采样镇定

贾金平，张凡娣

（天水师范学院 数学与统计学院，甘肃 天水 741001）

众所周知，在现代的工业自动化系统中，以计算机为核心的数字控制系统正逐步取代以模拟电路为主的模拟控制系统.和传统的模拟控制器相比，计算机控制不但可以实现许多高级复杂的控制算法，而且能够对远距离的设备进行统一的调度和控制.因此，作为计算机控制理论基础的采样系统理论成为了近年来控制领域的研究热点.国内外有很多控制论专家都投入到了这方面的研究，并形成了丰富的研究成果.[1-2]在采样系统中，控制器在每个采样时刻决定了从现在到下一采样时刻的控制量.如何为给定的连续时间系统设计采样控制器是采样系统理论的一个核心问题.对于线性系统，该问题已经得到了较好的解决.但对非线性系统，由于采样带来的复杂性，使得这一问题变得极具挑战性.大多数情况下，非线性采样系统的控制器设计都采用基于连续模型的设计方法.[3]该方法直接对连续控制器进行离散化.但研究表明，这种控制器只有在采样周期较小时才有效.为了得到在较大采样周期情况下能够保持理想控制性能的采样控制器.基于Lyapunov函数匹配的思想，Tiefensee等人对一类严格反馈非线性系统提出了一种具有幂级数形式的采样控制方案.[4]后来Tanasa将该方法推广到了多率采样控制的情形.[5]受这些结果的启发，本文对Tanasa的结果做了进一步的推广，在考虑输入延迟的情况下，对一类二阶严格反馈系统提出了一种基于预测器的多率控制方案.

1 预备知识

考虑具有如下形式的严格反馈非线性时滞系统

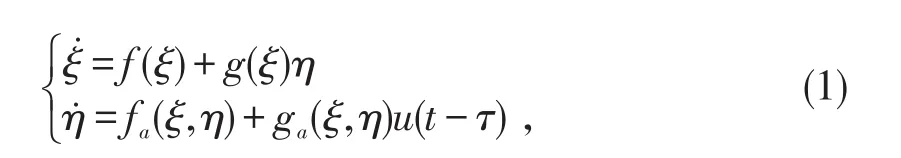
引理1.1考虑无延迟非线性系统(1)(即τ=0)，假设存在一个光滑函数η*=φ(ξ)和一个径向无界的正定函数 W(ξ)(W(0)=0)，使得

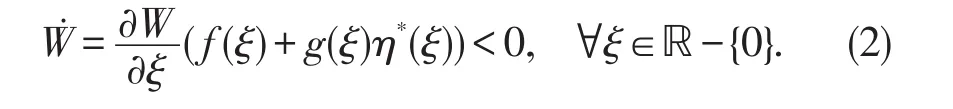
则在如下状态反馈控制器下

系统(1)的原点平衡状态(0,0)'是全局渐进稳定的.即 ，存 在 一 个 径 向 无 界 的 正 定 函 数 V(ξ,η)(V(0,0)=0)，使得对 ∀(ξ,η)∈ ℝ2-(0,0)，有

在设计连续控制器uc的过程中，令则无延迟系统(1)可被等价地写成

引理1.2考虑无延时系统(1)(即τ=0)，给定一个形如式(3)的光滑状态反馈控制器.则对一个充分小的，存在一个多率采样控制器这里

注意到，控制器(7)中的未知系数aij通过求解一个代数方程得到，它们的值可以看成是xk的函数，所以我们可以把该控制器简单的写成

2 控制器设计与分析

下面考虑输入延时系统(1)(即τ＞0)的采样镇定问题.在引理1.1和1.2的基础上，提出一种基于预测器的多率采样控制方案.为了保证系统解的存在性以及避免有限时间逃逸现象的发生，本文总假设对任意的初值和任意的控制输入，所涉及动态方程的解在整个时间轴上都是存在的.

定理2.1考虑非线性时滞系统(1)，给定一个形如式(3)的光滑状态反馈控制器.假设输入延时τ是采样周期的整数倍(即τ=Nδ).则对一个充分小的T*＞0 ，对任意的 δ∈[0,∞)，存在一个多率采样控制器

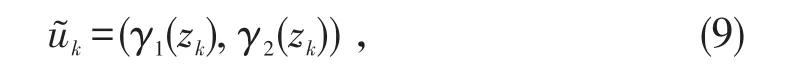
使得系统(1)的原点平衡状态(0,0)'是全局渐进稳定的.给定初始条件由下面方程产生

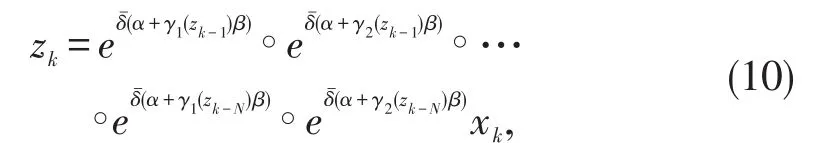
证明假设输入延时是采样周期的整数倍，即存在N∈ℕ，使得τ=Nδ.根据微分方程解的Lie-级数表示,[7]非线性时滞系统(1)的采样等价模型可以表示为

这里α和β是如(6)中一样所定义的光滑函数.通过引入中间变量，可以将时滞系统(11)转化为下面的无延迟系统

对系统(12)，根据引理1.1中的V构造下面的Lyapu⁃nov函数

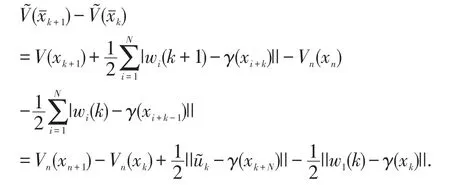
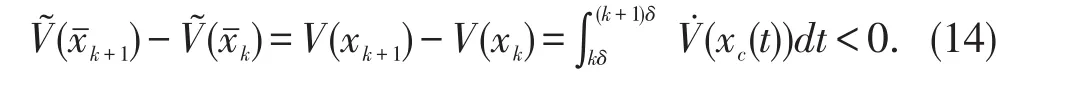
这说明系统(1)的离散等价系统是全局渐进稳定的.由假设知，对任意的t0≥0和任意的初始条件x(t0)，系统(5)的解 x(t)，t∈[0,+∞)存在.由 α(x)和 β(x)的连续性可知，系统(5)的解在任意闭区间上有界.这说明，与之等价的系统(1)的解是全局一致有界的.综合离散等价系统的全局渐进稳定性，应用文献[8]中的结果，可以证明，在多率采样控制器(9)-(10)下，时滞系统(1)的原点平衡点(0,0)是全局渐进稳定的.