高中数学教学中学生构造新函数的探析
广东省开平市第一中学 刘 宏
数学是一门逻辑性较强的学科,学生学习起来存在很多的困难,尤其是高中数学中的函数问题是高中数学教学中的一个重难点。要注重培养学生构造新函数解决函数问题的能力,帮助学生掌握联想、分析、转化等数学思想,通过对问题中的函数进行再构造来达到顺利解题的目的。结合教学经验,本文针对在高中数学教学中如何指导学生构造新函数来解决函数问题展开了一番探究,以供参考。
一、构造新函数的分类分析
1.直接构造
直接构造是指依照问题本身的直观结构对问题中的函数进行简单的变形处理,然后对变形之后的函数进行分析,得出解决问题的方法的函数构造方式。这是一种最基本、常见的构造新函数的方法,也是学生必须掌握的一种数学能力。
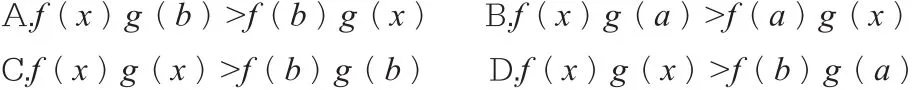

2.间接构造
当使用直接构造法会使问题变得更复杂时,学生就需要使用间接构造法,对问题中的原函数的内在联系和特征进行深入挖掘,突出重点,然后根据找到的重点进行较大程度的变形,在变形之后的内在联系和结构的基础上构造出可行的新函数,从而进行解题。间接构造对学生的数学能力要求较高。
类型一:关系式为“加”型(注意对x的符号进行讨论)

模型二:关系式为“减”型(注意对x的符号进行讨论)




二、提升学生构造新函数能力的对策
构造新函数是解决高中数学问题中经常会用到的一种方法,常见的问题有函数的单调性问题、方程根的问题、求最值的问题、不等式问题等。教师需要从多个角度锻炼学生构造新函数的能力,重视学生的基础和兴趣,使学生掌握快速解决函数问题的方法。
首先,夯实学生的知识点基础,培养学生多角度看待问题的能力。函数问题一直是高考的热点,并且随着新课程思想的全面渗透,高考对学生函数解题能力的要求也在不断提升,更加重视对学生灵活思维的考查。因此,在日常的教学过程中,教师要注重培养学生的发散性思维,使学生学会用多个角度看待问题,学会一题多解,养成灵活的思维习惯。
构造函数解决问题的方法并不是无迹可寻的,其存在着一定的技巧和原则。在日常的教学过程中,教师要注重总结学生在构造函数上存在的问题,积累教学经验,给予学生正确的构造技巧指导,科学地提升学生构造函数的能力。
培养学生快速构造新函数的能力是高中数学教学的重点,也是提升学生知识迁移能力、发散性思维、创新意识的重要途径,应当得到广大高中数学教师的足够重视。高中数学教师要站在学生的角度思考问题,了解高中生的学习需求和心理特征,以学生的整体协调发展为目标制定可行的培养计划,科学地提升学生构造新函数的能力,使学生面对函数问题时做到游刃有余,并在训练的过程中提升数学核心素养水平,形成完整的数学知识结构。

